الرسم البياني
الرسم البياني هو من بنى المعطيات غير الخطية والتي تتضمّن عقدًا nodes وأضلاع edges. تُسمّى العقد في بعض الأحيان بالرؤوس vertices والأضلاع بالخطوط lines أو الأقواس arcs التي تربط بين عقدتين في الرسم البياني.
ويمكن وصف الرسم البياني بصورة أدق بأنّه يحتوي على مجموعة محدّدة من العقد (أو الرؤوس) ومجموعة محدّدة من الأضلاع التي تربط بين عقدتين.
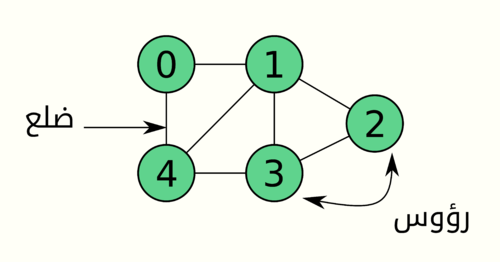
يتضمّن الرسم البياني أعلاه مجموعة الرؤوس V = {0,1,2,3,4} ومجموعة الأضلاع E = {01, 12, 23, 34, 04, 14, 13}.
يجدر التنبيه إلى أن مجموعة الحواف مرتّبة وذلك لأنّ الزوج (u, v) يختلف عن الزوج (v, u) في حال استخدام الرسم البياني الموجّه directed graph (أو ما يعرف اختصارًا بـ di-graph). يشير الزوج (u, v) إلى أنّ هناك حافة من الرأس u إلى الرأس v، ويمكن للحافة أن تتضمّن الوزن/القيمة/الكلفة.
تستخدم الرسوم البيانية لتمثيل الكثير من التطبيقات الواقعية، فمثلًا تستخدم الرسوم البيانية لتمثيل الشبكات، إذ يمكن للشبكات أن تضمّ العديد من المسارات في مدينة أو في شبكة للهاتف أو في دائرة كهربائية. وتستخدم الرسوم البيانية كذلك في الشبكات الاجتماعية مثل LinkedIn و فيسبوك. فعلى سبيل المثال يمثّل كل شخص في فيسبوك رأسًا (أو عقدة) في الرسم البياني، وكل عقدة في الرسم البياني عبارة عن بنية تتضمن معلومات ذلك الشخص مثل المعرّف والاسم والجنس ومحل الإقامة وغيرها.
تمثيل الرسوم البيانية
هناك طريقتان شائعتان لتمثيل الرسوم البيانية:
- مصفوفة المجاورة Adjacency Matrix.
- قائمة المجاورة Adjacency List.
وهناك طرق أخرى لتمثيل الرسوم البيانية مثل مصفوفة الوقوع Incidence Matrix أو قائمة الوقوع Incidence List. يعتمد اختيار طريقة التمثيل على الحالة التي يجري التعامل معها، وعلى العمليات المراد إجراؤها وسهولة الاستخدام.
مصفوفة المجاورة
مصفوفة المجاورة هي مصفوفة ثنائية الأبعاد حجمها V x V وتمثل V عدد الرؤوس في الرسم البياني. ولو فرضنا أنّ المصفوفة ثنائية الأبعاد تحمل الاسم adj فإنّ الموقع adj[i][j] = 1 يشير إلى أنّ هناك ضلعًا يربط الرأس i بالرأس j. تكون مصفوفات المجاورة التي تمثّل رسومًا بيانية غير موجّهةٍ متناظرةً دائمًا. تستخدم مصفوفات المجاورة كذلك في تمثيل الرسوم البيانية الموزونة، فلو كان الموقع adj[i][j] = w فإنّ هذا يعني أن هناك ضلعًا يربط الرأس i بالرأس j ولهذا الضلع الوزن w.
مصفوفة المجاورة للمثال أعلاه هي:

مميزات هذه الطريقة:
- سهولة التنفيذ والمتابعة.
- يبلغ التعقيد الزمني لعملية حذف ضلع من الأضلاع
O(1). - يمكن لعمليات الاستعلام عن وجود ضلع يربط الرأس u بالرأس v أن تكون فعّالة وأن تنفّذ في
O(1)من الوقت.
عيوب هذه الطريقة:
- تستهلك الكثير من المساحة
O(V^2)، وحتى لو تضمّن الرسم البياني القليل من الرؤوس (أي أن عدد الأضلاع قليل) فإنّ هذه الطريقة تستهلك المساحة ذاتها. - يبلغ التعقيد الزمني لعملية إضافة رأس إلى الرسم البياني
O(V^2).
أمثلة
يعرض المثال التالي طريقة تنفيذ مصفوفة المجاورة في لغة بايثون:
class Graph:
def __init__(self,numvertex):
self.adjMatrix = [[-1]*numvertex for x in range(numvertex)]
self.numvertex = numvertex
self.vertices = {}
self.verticeslist =[0]*numvertex
def set_vertex(self,vtx,id):
if 0<=vtx<=self.numvertex:
self.vertices[id] = vtx
self.verticeslist[vtx] = id
def set_edge(self,frm,to,cost=0):
frm = self.vertices[frm]
to = self.vertices[to]
self.adjMatrix[frm][to] = cost
# لا تضف هذا السطر إن كنت تستخدم الرسوم البيانية الموجّهة
self.adjMatrix[to][frm] = cost
def get_vertex(self):
return self.verticeslist
def get_edges(self):
edges=[]
for i in range (self.numvertex):
for j in range (self.numvertex):
if (self.adjMatrix[i][j]!=-1):
edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j]))
return edges
def get_matrix(self):
return self.adjMatrix
G =Graph(6)
G.set_vertex(0,'a')
G.set_vertex(1,'b')
G.set_vertex(2,'c')
G.set_vertex(3,'d')
G.set_vertex(4,'e')
G.set_vertex(5,'f')
G.set_edge('a','e',10)
G.set_edge('a','c',20)
G.set_edge('c','b',30)
G.set_edge('b','e',40)
G.set_edge('e','d',50)
G.set_edge('f','e',60)
print("Vertices of Graph")
print(G.get_vertex())
print("Edges of Graph")
print(G.get_edges())
print("Adjacency Matrix of Graph")
print(G.get_matrix())
قائمة المجاورة
تستخدم هذه الطريقة مصفوفة من القوائم، ويكون حجم المصفوفة مساويًا لعدد الرؤوس في الرسم البياني. ولو فرضنا أنّ المصفوفة تحمل الاسم array[] فإنّ العنصر array[i] يمثّل قائمة الرؤوس المجاورة للرأس i. يمكن استخدام طريقة التمثيل هذه مع الرسوم البيانية الموزونة، إذ يمكن تمثيل أوزان الأضلاع بواسطة قوائم من الأزواج.
يعرض الشكل التالي طريقة تمثيل الرسم البياني أعلاه باستخدام قائمة المجاورة:

أمثلة
تعرض الأمثلة التالية طريقة تنفيذ قائمة المجاورة في عدد من لغات البرمجة.
يجدر التنبيه إلى أنّ طرق التنفيذ أدناه تستخدم المصفوفات الديناميكية (المتجهات vector في C++ و ArrayList في جافا) عوضًا عن القوائم المترابطة لتمثيل قوائم المجاورة.
- C++:
#include<bits/stdc++.h>
using namespace std;
// دالة مساعدة لإضافة ضلع إلى رسم بياني غير موجّه
void addEdge(vector<int> adj[], int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
// دالة مساعدة لطباعة قائمة المجاورة التي تمثّل الرسم البياني
void printGraph(vector<int> adj[], int V)
{
for (int v = 0; v < V; ++v)
{
cout << "\n Adjacency list of vertex "
<< v << "\n head ";
for (auto x : adj[v])
cout << "-> " << x;
printf("\n");
}
}
// اختبار الدوال السابقة
int main()
{
int V = 5;
vector<int> adj[V];
addEdge(adj, 0, 1);
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
printGraph(adj, V);
return 0;
}
- بايثون:
# يستخدم هذا الصنف لتمثيل قائمة المجاورة الخاصّة بعقدة معينة
class AdjNode:
def __init__(self, data):
self.vertex = data
self.next = None
# يمثل هذا الصنف رسمًا بيانياً.
# الرسم البياني هو قائمة تتضمن قوائم المجاورة.
# عدد الرؤوس سيكون هو حجم المصفوفة.
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = [None] * self.V
# دالة لإضافة ضلع إلى الرسم البياني غير الموجّه
def add_edge(self, src, dest):
# إضافة العقدة إلى العقدة المصدرية
node = AdjNode(dest)
node.next = self.graph[src]
self.graph[src] = node
# إضافة العقدة المصدرية إلى الهدف الذي هو رسم بياني غير موجّه
node = AdjNode(src)
node.next = self.graph[dest]
self.graph[dest] = node
# دالة لطباعة الرسم البياني
def print_graph(self):
for i in range(self.V):
print("Adjacency list of vertex {}\n head".format(i), end="")
temp = self.graph[i]
while temp:
print(" -> {}".format(temp.vertex), end="")
temp = temp.next
print(" \n")
# اختبار الشيفرة السابقة
if __name__ == "__main__":
V = 5
graph = Graph(V)
graph.add_edge(0, 1)
graph.add_edge(0, 4)
graph.add_edge(1, 2)
graph.add_edge(1, 3)
graph.add_edge(1, 4)
graph.add_edge(2, 3)
graph.add_edge(3, 4)
graph.print_graph()
- جافا
import java.util.LinkedList;
public class GFG
{
// صنف معرّف من قبل المستخدم لتمثيل الرسم البياني
// الرسم البياني هو مصفوفة تتضمن قوائم المجاورة
// عدد الرؤوس في الرسم البياني سيكون هو حجم المصفوفة
static class Graph
{
int V;
LinkedList<Integer> adjListArray[];
// دالة بانية
Graph(int V)
{
this.V = V;
// تعريف حجم المصفوفة ليكون مساويًا عدد الرؤوس
adjListArray = new LinkedList[V];
// إنشاء قائمة جديدة لكل رأس
// وذلك ليكون بالإمكان تخزين العقد المتجاورة
for(int i = 0; i < V ; i++){
adjListArray[i] = new LinkedList<>();
}
}
}
// تضيف الدالة ضلعًا إلى الرسم البياني غير الموجّه
static void addEdge(Graph graph, int src, int dest)
{
// إضافة الضلع من المصدر إلى الهدف
graph.adjListArray[src].add(dest);
// لما كان الرسم البياني غير موجّه، نضيف ضلعًا من الهدف إلى المصدر أيضًا
graph.adjListArray[dest].add(src);
}
// دالة مساعدة لطباعة قائمة المجاورة التي تمثل الرسم البياني
static void printGraph(Graph graph)
{
for(int v = 0; v < graph.V; v++)
{
System.out.println("Adjacency list of vertex "+ v);
System.out.print("head");
for(Integer pCrawl: graph.adjListArray[v]){
System.out.print(" -> "+pCrawl);
}
System.out.println("\n");
}
}
// اختبار الدوال السابقة
public static void main(String args[])
{
// إنشاء الرسم البياني في الشكل أعلاه
int V = 5;
Graph graph = new Graph(V);
addEdge(graph, 0, 1);
addEdge(graph, 0, 4);
addEdge(graph, 1, 2);
addEdge(graph, 1, 3);
addEdge(graph, 1, 4);
addEdge(graph, 2, 3);
addEdge(graph, 3, 4);
// طباعة قائمة المجاورة التي تمثل الرسم البياني أعلاه
printGraph(graph);
}
}
مميزات هذه الطريقة:
- تمتاز طريقة التمثيل هذه بتوفير المساحة
O(|V|+|E|). وفي أسوأ الاحتمالات يمكن أن يكون هناكC(V, 2)من الأضلاع في الرسم البياني وبهذا تكون المساحة المستهلكةO(V^2). - إضافة الرؤوس إلى الرسم البياني أكثر سهولة.
عيوب هذه الطريقة:
عمليات الاستعلام عن وجود ضلع يربط الرأس u بالرأس v غير فعّالة وتنفّذ في O(V) من الوقت.
التنقل بالعرض أولًا في الرسوم البيانية
التنقل (أو البحث) بالعرض أولًا في الرسوم البيانية مشابهة إلى حدّ كبير لعملية النتقل بالعرض أولًا في الأشجار الثنائية، والفرق الوحيد بينهما هو أنّ الرسوم البيانية، وبخلاف الأشجار الثنائية، يمكن أن تحتوي على دورات cycles وهكذا يمكن العودة إلى نفس العقدة مرة أخرى، ولتجنب معالجة العقدة نفسها أكثر من مرة، تُستخدم مصفوفة من القيم البوليانية (المنطقية) للعقد المزورة أثناء المعالجة.
فعلى سبيل المثال نبدأ في الرسم البياني التالي من العقدة 2، وعند الوصول إلى العقدة 0 نبحث عن جميع العقد المجاورة لها، ولكن العقدة 2 مجاورة لها أيضًا، وإن لم ننشئ مصفوفة للعقد التي تمت زيارتها فإنّ العقدة 2 ستعالجة مرة أخرى وسندخل في عملية لا نهائية.
يؤدي تنفيذ عملية البحث بالعرض أولًا على الرسم البياني أعلاه إلى الحصول على النتيجة التالية: 2, 0, 3, 1.
أمثلة
تعرض الأمثلة التالية طريقة تنفيذ هذه العملية وفي عدد من لغات البرمجة.
تستخدم هذه الأمثلة طريقة قائمة المجاورة adjacency list لتمثيل الرسوم البيانية. ويُستخدم list container في مكتبة القوالب القياسية STL لتخزين قوائم العقد المجاورة ورتل العقد المطلوبة في عملية البحث بالعرض أولًا.
- C++:
#include<iostream>
#include <list>
using namespace std;
// يمثل هذا الصنف رسمًا بيانيًا موجّهًا
// وذلك باستخدام طريقة قائمة المجاورة
class Graph
{
int V; // عدد العقد
// مؤشر إلى مصفوفة تحتوي على قوائم المجاورة
list<int> *adj;
public:
Graph(int V); // دالة بانية
// دالة لإضافة ضلع إلى الرسم البياني
void addEdge(int v, int w);
// تطبع الدالة ناتج عملية البحث بالعرض أولًا للمصدر المعطى
void BFS(int s);
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // إضافة w إلى قائمة v.
}
void Graph::BFS(int s)
{
// تعليم جميع الرؤوس على أنّها غير مزورة
bool *visited = new bool[V];
for(int i = 0; i < V; i++)
visited[i] = false;
// إنشاء رتل لإجراء عملية البحث بالعرض أولًا
list<int> queue;
// تعليم العقدة الحالية على أنّها مزورة وإدراجها في الرتل
visited[s] = true;
queue.push_back(s);
// 'i' للحصول على جميع الرؤوس المجاورة لرأس معين سنستخدم
list<int>::iterator i;
while(!queue.empty())
{
// إزالة رأس من الرتل وطباعته
s = queue.front();
cout << s << " ";
queue.pop_front();
// الحصول على جميع الرؤوس المجاورة للرأس المزال
// إن لم تكن الرؤوس المجاورة مزورة
// فسنعلّمها على أنّها مزورة وندرجها في الرتل
for (i = adj[s].begin(); i != adj[s].end(); ++i)
{
if (!visited[*i])
{
visited[*i] = true;
queue.push_back(*i);
}
}
}
}
// اختبار التوابع السابقة
int main()
{
// إنشاء الرسم البياني في الشكل أعلاه
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
cout << "Following is Breadth First Traversal "
<< "(starting from vertex 2) \n";
g.BFS(2);
return 0;
}
- بايثون
from collections import defaultdict
# يمثّل هذا الصنف رسمًا بيانياً موجّهًا
# وذلك باستخدام طريقة قائمة المجاورة
class Graph:
# دالة بانية
def __init__(self):
# استخدام القاموس الافتراضي لتخزين الرسم البياني
self.graph = defaultdict(list)
# دالة لإضافة ضلع إلى الرسم البياني
def addEdge(self,u,v):
self.graph[u].append(v)
# دالة لطباعة نتيجة عملية البحث بالعرض أولًا في الرسم البياني
def BFS(self, s):
# تعليم جميع الرؤوس على أنّها مزورة
visited = [False] * (len(self.graph))
# إنشاء رتل لإجراء عملية البحث بالعرض أولًا
queue = []
# تعليم العقدة المصدرية على أنّها مزورة
# ثم إدراجها في الرتل
queue.append(s)
visited[s] = True
while queue:
# إزالة الرأس من الرتل وطباعة قيمته
s = queue.pop(0)
print (s, end = " ")
# الحصول على جميع العقد المجاورة
# للرأس المزال. إن لم تكون العقدة المجاورة
# مزورة فسنعلّمها على أنّها مزورة وندرجها في الرتل
for i in self.graph[s]:
if visited[i] == False:
queue.append(i)
visited[i] = True
# اختبار الدوال السابقة
# إنشاء رسم بياني من الشكل السابق
g = Graph()
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
print ("Following is Breadth First Traversal"
" (starting from vertex 2)")
g.BFS(2)
- جافا
import java.io.*;
import java.util.*;
// يمثّل هذا الصنف رسمًا بيانياً موجّها وذلك باستخدام طريقة قائمة المجاورة
class Graph
{
private int V; // عدد الرؤوس
private LinkedList<Integer> adj[]; //قوائم المجاورة
// دالة بانية
Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
// دالة لإضافة ضلع في الرسم البياني
void addEdge(int v,int w)
{
adj[v].add(w);
}
// دالة لطباعة نتيجة عملية البحث بالعرض أولًا في المصدر المعطى
void BFS(int s)
{
// تعليم جميع الرؤوس على أنّها غير مزورة
boolean visited[] = new boolean[V];
// إنشاء رتل لإجراء عملية البحث بالعرض أولًا
LinkedList<Integer> queue = new LinkedList<Integer>();
// تعليم العقدة الحالية على أنّها مزورة وإدراجها في الرتل
visited[s]=true;
queue.add(s);
while (queue.size() != 0)
{
// إزالة رأس من الرتل وطباعة قيمته
s = queue.poll();
System.out.print(s+" ");
// الحصول على جميع الرؤوس المجاورة للرأس المزال
// إن كانت العقدة المجاورة غير مزورة، فسنعلّمها
// على أنّها مزورة وندرجها في الرتل
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext())
{
int n = i.next();
if (!visited[n])
{
visited[n] = true;
queue.add(n);
}
}
}
}
// اختبار الدوال السابقة
public static void main(String args[])
{
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.println("Following is Breadth First Traversal "+
"(starting from vertex 2)");
g.BFS(2);
}
}
لاحظ أنّ الشيفرات السابقة تتنقل فقط عبر الرؤوس التي يمكن الوصول إليها من الرأس المعطى. هناك حالات لا يمكن فيها الوصول إلى أيّ رأس انطلاقًا من الرأس المعطى (مثل الرسم االبياني المفصول). يمكن تعديل دالة BFS لطباعة جميع العقد وذلك بإجراء عملية التنقل بدءًا من جميع العقد واحدة تلو الأخرى.
التعقيد الزمني
بيلغ التعقيد الزمني لهذه العملية O(V+E) إذ تمثّل V عدد الرؤوس و E عدد الأضلاع في الرسم البياني.
تطبيقات عملية البحث بالعرض أولًا
يمكن الاستفادة من عملية البحث بالعرض أولًا في العديد من التطبيقات منها:
- إيجاد المسار الأقصر والشجرة الممتدة الصغرى Minimum Spanning Tree للرسوم البيانية غير الموزونة: في الرسوم البيانية غير الموزونة، يكون المسار الأقصر هو المسار الذي يمر عبر أقل عدد من الأضلاع، وهذا هو الطريق المتّبع في عملية البحث بالعرض أولًا، إذ يتم الوصول إلى رأس معين في الرسم البياني ابتداءً من مصدر معين وباستخدام أقل عدد من الأضلاع. كذلك الأمر فإنّ أيّ شجرة ممتدة في الرسوم البيانية غير الموزونة هي شجرة ممتدة صغرى، ويمكن استخدام عملية البحث بالعمق أولًا أو بالعرض أولًا لإيجاد الشجرة الممتدة.
- شبكات نظير بنظير peer to peer: تستخدم عملية البحث بالعرض أولًا في شبكات نظير بنظير مثل BitTorrent للعثور على جميع العقد المجاورة.
- الزواحف Crawlers في محركات البحث: تبني الزواحف فهاسرها باستخدام عملية البحث بالعرض أولًا. وتتلخص الفكرة في أن تبدأ عملية البحث من صفحة معيّنة ثم تتبّع جميع الروابط من المصدر والاستمرار بالقيام بذلك. يمكن استخدام طريقة البحث بالعمق أولًا ولكن تمتاز طريقة البحث بالعرض أولًا بأنّ عمق أو مستوى الشجرة المبنية يكون محدودًا.
- مواقع التواصل الاجتماعي: يمكن العثور على الأشخاص في مواقع التواصل الاجتماعي وضمن مسافة معيّنة من شخص معيّن باستخدام عملية البحث بالعرض أولًا.
- أنظمة الملاحة العالمية GPS: تستخدم عملية البحث بالعرض أولًا للعثور على جميع المواقع المجاورة لموقع معين.
- البث في الشبكة: تتبع حزمة البث عملية البحث بالعرض أولًا للوصول إلى جميع العقد.
- جمع الموارد غير المستخدمة Garbage Collection: تستخدم عملية البحث بالعرض أولًا لنسخ الموارد غير المستخدمة بواسطة خوارزمية Cheney. تفضل عملية البحث بالعرض أولًا على البحث بالعمق أولًا لأنّها تعطي موقعية locality أفضل للإشارات references.
- الكشف عن الدوائر في الرسوم البيانية غير الموجهة: يمكن استخدام عملية البحث بالعرض أولًا أو بالعمق أولًا للكشف عن الدوائر في الرسوم البيانية، ولكن لا يمكن استخدام طريقة البحث بالعرض أولًا في الرسوم البيانية الموجّهة.
- خوارزمية Ford-Fulkerson: يمكن استخدام طريقتي البحث في هذه الخوارزمية لإيجاد التدفق الأعظم maximum flow. ولكن يفضل استخدام عملية البحث بالعرض أولًا لأنّها تقلص التعقيد الزمني في أسوأ الحالات إلى O(VE2).
- التحقق من أن الرسم البياني يتكون من قسمين Bipartite: يمكن استخدام كلا طريقتي البحث.
- إيجاد المسار: يمكن استخدام طريقتي البحث لمعرفة ما إذا كان هناك مسار يربط بين رأسين معينين.
- إيجاد جميع العقد في مكون واحد مترابط: يمكن استخدام عمليتي البحث لإيجاد جميع العقد التي يمكن الوصول إليها من العقدة المعطاة.
إضافة إلى ما سبق من تطبيقات تدخل عملية البحث بالعرض أولًا في العديد من الخوارزميات مثل خوارزمية Prim للشجرة الممتدة الصغرى، وخوارزمية Dijkstra لإيجاد المسار الأقصر من مصدر واحد.
البحث بالعمق أولًا في الرسوم البيانية
التنقل (أو البحث) بالعمق أولًا في الرسوم البيانية مشابه إلى حدٍّ كبير لعملية النتقل بالعمق أولًا في الأشجار الثنائية، والفرق الوحيد بينهما هو أنّ الرسوم البيانية، وبخلاف الأشجار الثنائية، يمكن أن تحتوي على دورات cycles وهكذا يمكن العودة إلى نفس العقدة مرة أخرى، ولتجنب معالجة العقدة نفسها أكثر من مرة، تُستخدم مصفوفة من القيم البوليانية (المنطقية) للعقد المزورة أثناء المعالجة.
فعلى سبيل المثال نبدأ في الرسم البياني التالي من العقدة 2، وعند الوصول إلى العقدة 0 نبحث عن جميع العقد المجاورة لها، ولكن العقدة 2 مجاورة لها أيضًا، وإن لم ننشئ مصفوفة للعقد التي تمت زيارتها فإنّ العقدة 2 ستعالجة مرة أخرى وسندخل في عملية لا نهائية.
يؤدي تنفيذ عملية البحث بالعرض أولًا على الرسم البياني أعلاه إلى الحصول على النتيجة التالية: 2, 0, 1, 3.
أمثلة
تعرض الأمثلة التالية طريقة تنفيذ هذه العملية وفي عدد من لغات البرمجة.
تستخدم هذه الأمثلة طريقة قائمة المجاورة adjacency list لتمثيل الرسوم البيانية. ويُستخدم list container في مكتبة القوالب القياسية STL لتخزين قوائم العقد المجاورة ورتل العقد المطلوبة في عملية البحث بالعرض أولًا.
- C++:
#include<iostream>
#include <list>
using namespace std;
// يمثل هذا الصنف رسمًا بيانيًا موجّهًا
// وذلك باستخدام طريقة قائمة المجاورة
class Graph
{
int V; // عدد العقد
// مؤشر إلى مصفوفة تحتوي على قوائم المجاورة
list<int> *adj;
public:
Graph(int V); // دالة بانية
// دالة لإضافة ضلع إلى الرسم البياني
void addEdge(int v, int w);
// تطبع الدالة ناتج عملية البحث بالعمق أولًا للمصدر المعطى
void DFS(int s);
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // إضافة w إلى قائمة v.
}
void Graph::DFSUtil(int v, bool visited[])
{
// تعليم العقدة الحالية على أنّها مزورة وطباعة قيمتها
visited[v] = true;
cout << v << " ";
// تنفيذ الدالة تعاوديًا على جميع الرؤوس المجاورة لهذه الرأس
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
DFSUtil(*i, visited);
}
// البحث بالعمق أولًا عن الرؤوس التي يمكن الوصول إليها من الرأس المعطى
// هذه الدالة تعاودية
void Graph::DFS(int v)
{
// تعليم جميع الرؤوس على أنّها غير مزورة
bool *visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
// استدعاء الدالة المساعدة التعاودية لطباعة
// نتيجة عملية البحث بالعمق أولًا
DFSUtil(v, visited);
}
int main()
{
// إنشاء الرسم البياني بالاعتماد على الشكل أعلاه
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
cout << "Following is Depth First Traversal"
" (starting from vertex 2) \n";
g.DFS(2);
return 0;
}
- بايثون:
from collections import defaultdict
# يمثّل هذا الصنف رسمًا بيانياً موجّهًا
# وذلك باستخدام طريقة قائمة المجاورة
class Graph:
# دالة بانية
def __init__(self):
# استخدام القاموس الافتراضي لتخزين الرسم البياني
self.graph = defaultdict(list)
# دالة لإضافة ضلع إلى الرسم البياني
def addEdge(self,u,v):
self.graph[u].append(v)
# دالة مساعدة
def DFSUtil(self,v,visited):
# تعليم العقدة الحالية على أنّها مزورة وطباعة قيمتها
visited[v]= True
print v,
# تنفيذ الدالة تعاوديًا على جميع الرؤوس المجاورة لهذا الرأس
for i in self.graph[v]:
if visited[i] == False:
self.DFSUtil(i, visited)
# دالة لطباعة نتيجة عملية البحث بالعرض أولًا في الرسم البياني
def DFS(self,v):
# تعليم جميع الرؤوس على أنها غير مزورة
visited = [False]*(len(self.graph))
# استدعاء الدالة المساعدة التعاودية لطباعة
# نتيجة عملية التنقل بالعمق أولًا
self.DFSUtil(v,visited)
# اختبار الدوال السابقة
# إنشاء الرسم البياني من الشكل السابق
g = Graph()
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
print "Following is DFS from (starting from vertex 2)"
g.DFS(2)
- جافا
import java.io.*;
import java.util.*;
// يمثّل هذا الصنف رسمًا بيانياً موجّها وذلك باستخدام طريقة قائمة المجاورة
class Graph
{
private int V; // عدد الرؤوس
// مصفوفة من القوائم تستخدم لتمثيل الرسم البياني بطريقة قائمة المجاورة
private LinkedList<Integer> adj[];
// دالة بانية
Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
// دالة لإضافة ضلع في الرسم البياني
void addEdge(int v, int w)
{
adj[v].add(w);
}
// دالة مساعدة
void DFSUtil(int v,boolean visited[])
{
// تعليم العقدة الحالية على أنّها مزورة وطباعتها
visited[v] = true;
System.out.print(v+" ");
// تنفيذ الدالة تعاوديًا على جميع الرؤوس المجاورة لهذا الرأس
Iterator<Integer> i = adj[v].listIterator();
while (i.hasNext())
{
int n = i.next();
if (!visited[n])
DFSUtil(n, visited);
}
}
// تجري هذه الدالة عملية البحث بالعمق أولًا
// وتستفيد من الدالة المساعدة
void DFS(int v)
{
// تعليم جميع الرؤوس على أنّها غير مزورة
boolean visited[] = new boolean[V];
// استدعاء الدالة المساعدة التعاودية لطباعة نتيجة عملية البحث بالعمق أولاً
DFSUtil(v, visited);
}
public static void main(String args[])
{
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.println("Following is Depth First Traversal "+
"(starting from vertex 2)");
g.DFS(2);
}
}
تعطي الشيفرات السابقة المخرجات التالية:
Following is Depth First Traversal (starting from vertex 2)
2 0 1 3
التعامل مع الرسوم البيانية المقطوعة disconnected
تتنقل الشيفرات السابقة بين العقد التي يمكن الوصول إليها من العقدة المصدرية. ولكن قد لا يكون من الممكن الوصول إلى جميع العقد في بعض الحالات (مثل الرسم البياني المقطوع). يجب استدعاء الدالة DFSUtil() لكل عقدة في الرسم البياني وذلك لإجراء عملية بحث كاملة، ولكن يجب التحقّق كذلك من أن العقدة لم تطبع من قبل بواسطة استدعاء سابق للدالة DFSUtil().
تعرض الأمثلة التالية طريقة تنفيذ عملية البحث على الرسم البياني بأكمله حتى لو كانت هناك عقد لا يمكن الوصول إليها.
- C++:
#include<iostream>
#include <list>
using namespace std;
class Graph
{
int V; // عدد الرؤوس
list<int> *adj; // مؤشر إلى مصفوفة تحتوي على قوائم المجاورة
void DFSUtil(int v, bool visited[]); // دالة مساعدة
public:
Graph(int V); // دالة بانية
void addEdge(int v, int w); // دالة لإضافة ضلع إلى الرسم البياني
void DFS(); // تطبع الدالة نتيجة عملية البحث بالعمق أولًا للرسم البياني بأكمله
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
}
void Graph::DFSUtil(int v, bool visited[])
{
// تعليم العقدة الحالية على انّها مزورة وطباعة قيمتها
visited[v] = true;
cout << v << " ";
// تنفيذ الدالة تعاوديًا على جميع الرؤوس المجاورة لهذا الرأس
list<int>::iterator i;
for(i = adj[v].begin(); i != adj[v].end(); ++i)
if(!visited[*i])
DFSUtil(*i, visited);
}
// تنفذ هذه الدالة عملية البحث بالعمق أولًا وتستفيد من الدالة المساعدة
void Graph::DFS()
{
// تعليم جميع الرؤوس على أنّها غير مزورة
bool *visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
// استدعاء الدالة المساعدة التعاودية لطباعة نتيجة عملية البحث بالعمق أولًا
// على جميع الرؤوس واحدًا تلو الآخر
for (int i = 0; i < V; i++)
if (visited[i] == false)
DFSUtil(i, visited);
}
int main()
{
// إنشاء الرسم البياني في الشكل أعلاه
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
cout << "Following is Depth First Traversaln";
g.DFS();
return 0;
}
- بايثون:
from collections import defaultdict
# يمثّل هذا الصنف رسمًا بيانياً موجّهًا
# وذلك باستخدام طريقة قائمة المجاورة
class Graph:
# دالة بانية
def __init__(self):
# استخدام القاموس الافتراضي لتخزين الرسم البياني
self.graph = defaultdict(list)
# دالة لإضافة ضلع إلى الرسم البياني
def addEdge(self,u,v):
self.graph[u].append(v)
# دالة مساعدة
def DFSUtil(self, v, visited):
# تعليم العقدة الحالية على أنّها مزورة وطباعة قيمتها
visited[v]= True
print v,
# تنفيذ الدالة تعاوديًا على جميع الرؤوس المجاورة لهذا الرأس
for i in self.graph[v]:
if visited[i] == False:
self.DFSUtil(i, visited)
# تنفذ هذه الدالة عملية البحث بالعمق أولًا
# وتستفيد من الدالة المساعدة
def DFS(self):
V = len(self.graph) #العدد الكلي للرؤوس
# تعليم جميع الرؤوس على أنّها غير مزورة
visited =[False]*(V)
# استدعاء الدالة المساعدة التعاودية لطباعة
# نتيجة عملية البحث بالعمق أولًا على جميع الرؤوس
# واحدًا تلو الآخر
for i in range(V):
if visited[i] == False:
self.DFSUtil(i, visited)
# اختبار الدوال السابقة
# إنشاء الرسم البياني من الشكل السابق
g = Graph()
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
print "Following is DFS from (starting from vertex 2)"
g.DFS()
- جافا
import java.io.*;
import java.util.*;
// يمثّل هذا الصنف رسمًا بيانياً موجّها وذلك باستخدام طريقة قائمة المجاورة
class Graph
{
private int V; // عدد الرؤوس
// مصفوفة من القوائم تستخدم لتمثيل الرسم البياني بطريقة قائمة المجاورة
private LinkedList<Integer> adj[];
// دالة بانية
Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
// دالة لإضافة ضلع في الرسم البياني
void addEdge(int v, int w)
{
adj[v].add(w);
}
// دالة مساعدة
void DFSUtil(int v,boolean visited[])
{
// تعليم العقدة الحالية على أنّها مزورة وطباعة قيمتها
visited[v] = true;
System.out.print(v+" ");
// تنفيذ الدالة تعاوديًا على جميع الرؤوس المجاورة لهذا الرأس
Iterator<Integer> i = adj[v].listIterator();
while (i.hasNext())
{
int n = i.next();
if (!visited[n])
DFSUtil(n, visited);
}
}
// تنفذ الدالة عملية البحث بالعمق أولًا، وتستفيد من الدالة المساعدة
void DFS(int v)
{
// تعليم جميع الرؤوس على أنّها غير مزورة
boolean visited[] = new boolean[V];
// استدعاء الدالة التعاودية المساعدة لطباعة نتيجة عملية البحث بالعمق أولًا
DFSUtil(v, visited);
}
public static void main(String args[])
{
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.println("Following is Depth First Traversal "+
"(starting from vertex 2)");
g.DFS(2);
}
}
التعقيد الزمني
التعقيد الزمني لهذه العملية يبلغ O(V+E) وتمثّل V عدد الرؤوس و E عدد الأضلاع في الرسم البياني.
تطبيقات عملية البحث بالعمق أولًا
- تنتج عملية البحث بالعمق أولًا في الرسم البياني غير الموزون الشجرة الممتدة الصغرى والمسار الأقصر لجميع الأزواج في الشجرة all pair shortest path tree.
- الكشف عن الدوائر في الرسوم البيانية: يمتلك الرسم البياني إذا وفقط إذا رأينا ضلعًا خلفياً أثناء تنفيذ عملية البحث بالعمق أولًا.
- إيجاد المسار: يمكن تخصيص خوارزمية البحث بالعمق أولًا لإيجاد المسار بين رأسين معيّنين (u و z مثلًا) وكما يلي:
- نستدعي الدالة
DFS(G,u)وتمرير u كنقطة بداية. - نستخدم مكدسًا (ليكن اسمه S) لمتابعة المسار بين نقطة البداية والنقطة الحالية.
- بمجرد الوصول إلى نقطة الهدف z نعيد المسار الذي حصلنا عليه وهو عبارة عن محتويات المكدس.
- نستدعي الدالة
- الترتيب الطوبولوجي Topological Sorting: يستخدم هذا النوع من الترتيب في جدولة الأعمال من اعتمادية معطاة. يظهر هذا النوع من البرامج في علوم الحاسبات في عمليات جدولة التعلميات، و ترتيب معالجة صيغ الخلايا عند إعادة حساب الصيغ في جداول البيانات، والتخليق المنطقي، وتحديد ترتيب مهام التصريف التي يجب تنفيذها في ملفات makefiles، وفي سَلسَلة البيانات، وفي تحليل اعتماديات الرموز Symbol dependencies في الروابط linkers.
- حل الأحاجي التي تمتلك حلًّا واحدًا: مثل المتاهات. (يمكن تعديل عملية البحث بالعمق أولًا للعثور على جميع الحلول لمتاهة معينة وذلك بإضافة العقد الموجودة في المسار الحالي إلى مجموعة العقد المزورة).
مصادر
- صفحة Graph Data Structure and Algorithms في توثيق بنى المعطيات في موقع GeeksforGeeks.
- صفحة Graph and its representations في توثيق بنى المعطيات في موقع GeeksforGeeks.
- صفحة Breadth First Search or BFS for a Graph في توثيق بنى المعطيات في موقع GeeksforGeeks.
- صفحة Applications of Breadth First Traversal في توثيق بنى المعطيات في موقع GeeksforGeeks.
- صفحة Depth First Search or DFS for a Graph في توثيق بنى المعطيات في موقع GeeksforGeeks.
- صفحة Applications of Depth First Search في توثيق بنى المعطيات في موقع GeeksforGeeks.