الفرق بين المراجعتين لصفحة: «Algorithms/detect cycle»
لا ملخص تعديل |
لا ملخص تعديل |
||
| (1 مراجعات متوسطة بواسطة نفس المستخدم غير معروضة) | |||
| سطر 1: | سطر 1: | ||
<noinclude>{{DISPLAYTITLE:الكشف عن وجود دورة في الرسم البياني}}</noinclude> | يحتوي الرسم البياني على دورة إذا كان يحتوي على ضلع خلفي back edge، والمقصود بالضلع الخلفي الضلع الذي يخرج من العقدة ويعود إليها (حلقة-ذاتية) أو إلى أحد أسلافها في الشجرة الناتجة من عملية البحث بالعمق أولًا. | ||
يحتوي الرسم البياني التالي على ثلاثة أضلاع خلفية معلمة بعلامة x. | |||
[[ملف:cycle.png|مركز|481x481بك]] | |||
يمكن ملاحظة أن وجود ثلاثة أضلاع خلفية في الرسم البياني يشير إلى وجود ثلاث دورات فيه.<noinclude>{{DISPLAYTITLE:الكشف عن وجود دورة في الرسم البياني}}</noinclude> | |||
== الكشف عن وجود دورة في الرسم البياني الموجّه == | == الكشف عن وجود دورة في الرسم البياني الموجّه == | ||
| سطر 6: | سطر 11: | ||
يمكن استخدام عملية [[Algorithms/graphs#.D8.A7.D9.84.D8.A8.D8.AD.D8.AB .D8.A8.D8.A7.D9.84.D8.B9.D9.85.D9.82 .D8.A3.D9.88.D9.84.D9.8B.D8.A7 .D9.81.D9.8A .D8.A7.D9.84.D8.B1.D8.B3.D9.88.D9.85 .D8.A7.D9.84.D8.A8.D9.8A.D8.A7.D9.86.D9.8A.D8.A9|البحث بالعمق أولًا Depth First Search]] للكشف عن وجود دورة في الرسم البياني. تنتج عملية البحث بالعمق أولًا شجرة عند إجرائها على الرسم البياني المتصل. | يمكن استخدام عملية [[Algorithms/graphs#.D8.A7.D9.84.D8.A8.D8.AD.D8.AB .D8.A8.D8.A7.D9.84.D8.B9.D9.85.D9.82 .D8.A3.D9.88.D9.84.D9.8B.D8.A7 .D9.81.D9.8A .D8.A7.D9.84.D8.B1.D8.B3.D9.88.D9.85 .D8.A7.D9.84.D8.A8.D9.8A.D8.A7.D9.86.D9.8A.D8.A9|البحث بالعمق أولًا Depth First Search]] للكشف عن وجود دورة في الرسم البياني. تنتج عملية البحث بالعمق أولًا شجرة عند إجرائها على الرسم البياني المتصل. | ||
أما في حالة الرسم البياني غير المتصل disconnected فإن النتيجة هي مجموعة من الأشجار التي تعرف بغابة DFS Forest، وللكشف عن وجود الدورات يمكن التحقق من وجود الأضلاع الخلفية في كل شجرة على حدة. | أما في حالة الرسم البياني غير المتصل disconnected فإن النتيجة هي مجموعة من الأشجار التي تعرف بغابة DFS Forest، وللكشف عن وجود الدورات يمكن التحقق من وجود الأضلاع الخلفية في كل شجرة على حدة. | ||
| سطر 18: | سطر 16: | ||
للتحقق من وجود الضلع الخلفي يمكن متابعة الرؤوس الموجودة كدس التعاود recursion stack الخاص بالدالة في عملية التنقل بالعمق أولًا. فإن وصلنا إلى رأس موجود فعلًا في مكدس التعاود، فهذا يعني أنّ الشجرة تحتوي على دورة. إن الضلع الذي يربط العقدة الحالية بالعقدة الموجودة في مكدس التعاود هو ضلع خلفي. | للتحقق من وجود الضلع الخلفي يمكن متابعة الرؤوس الموجودة كدس التعاود recursion stack الخاص بالدالة في عملية التنقل بالعمق أولًا. فإن وصلنا إلى رأس موجود فعلًا في مكدس التعاود، فهذا يعني أنّ الشجرة تحتوي على دورة. إن الضلع الذي يربط العقدة الحالية بالعقدة الموجودة في مكدس التعاود هو ضلع خلفي. | ||
== | === تنفيذ الخوارزمية === | ||
تعرض الأمثلة التالية طريقة تنفيذ هذه الخوارزمية في عدد من لغات البرمجة: | تعرض الأمثلة التالية طريقة تنفيذ هذه الخوارزمية في عدد من لغات البرمجة: | ||
| سطر 262: | سطر 260: | ||
التعقيد الزمني لهذه العملية مشابه للتعقيد الزمني لعملية البحث بالعمق أولًا وهي <code>O(V+E)</code>. | التعقيد الزمني لهذه العملية مشابه للتعقيد الزمني لعملية البحث بالعمق أولًا وهي <code>O(V+E)</code>. | ||
== الكشف عن وجود دورة في الرسم البياني غير الموجّه | == الكشف عن وجود دورة في الرسم البياني غير الموجّه - خوارزمية "وحّد-جد" == | ||
المجموعة المفككة disjoint-set هي إحدى بنى المعطيات التي تتابع مجموعة من العناصر المقسّمة إلى عدد من المجاميع الفرعية (غير المتداخلة) المفككة. تجري خوارزمية وحّد-جِدْ union-find عمليتين مفيدتين على المجموعات المفككة، وهما: | المجموعة المفككة disjoint-set هي إحدى بنى المعطيات التي تتابع مجموعة من العناصر المقسّمة إلى عدد من المجاميع الفرعية (غير المتداخلة) المفككة. تجري خوارزمية وحّد-جِدْ union-find عمليتين مفيدتين على المجموعات المفككة، وهما: | ||
| سطر 291: | سطر 287: | ||
الضلع <code>0-2</code>: الرأس <code>0</code> موجود في المجموعة الفرعية <code>2</code> والرأس <code>2</code> موجود كذلك في المجموعة الفرعية <code>2</code>. نستنتج من ذلك أنّ هذا الضلع يشكّل دورة. | الضلع <code>0-2</code>: الرأس <code>0</code> موجود في المجموعة الفرعية <code>2</code> والرأس <code>2</code> موجود كذلك في المجموعة الفرعية <code>2</code>. نستنتج من ذلك أنّ هذا الضلع يشكّل دورة. | ||
== تنفيذ الخوارزمية == | === تنفيذ الخوارزمية === | ||
تعرض الأمثلة التالية طريقة تنفيذ خوارزمية وحّدِ-جِد في عدد من لغات البرمجة. | تعرض الأمثلة التالية طريقة تنفيذ خوارزمية وحّدِ-جِد في عدد من لغات البرمجة. | ||
المراجعة الحالية بتاريخ 18:30، 19 نوفمبر 2019
يحتوي الرسم البياني على دورة إذا كان يحتوي على ضلع خلفي back edge، والمقصود بالضلع الخلفي الضلع الذي يخرج من العقدة ويعود إليها (حلقة-ذاتية) أو إلى أحد أسلافها في الشجرة الناتجة من عملية البحث بالعمق أولًا.
يحتوي الرسم البياني التالي على ثلاثة أضلاع خلفية معلمة بعلامة x.
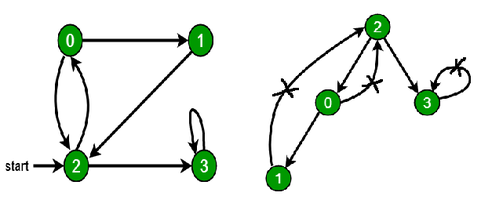
يمكن ملاحظة أن وجود ثلاثة أضلاع خلفية في الرسم البياني يشير إلى وجود ثلاث دورات فيه.
الكشف عن وجود دورة في الرسم البياني الموجّه
الهدف من هذه الخوارزمية هو الكشف عن وجود دورة في الرسم البياني الموجّه. فعلى سبيل المثال يحتوي الرسم البياني التالي على ثلاثة دورات هي 0->2->0 و 0->1->2->0 و 3->3.
يمكن استخدام عملية البحث بالعمق أولًا Depth First Search للكشف عن وجود دورة في الرسم البياني. تنتج عملية البحث بالعمق أولًا شجرة عند إجرائها على الرسم البياني المتصل.
أما في حالة الرسم البياني غير المتصل disconnected فإن النتيجة هي مجموعة من الأشجار التي تعرف بغابة DFS Forest، وللكشف عن وجود الدورات يمكن التحقق من وجود الأضلاع الخلفية في كل شجرة على حدة.
للتحقق من وجود الضلع الخلفي يمكن متابعة الرؤوس الموجودة كدس التعاود recursion stack الخاص بالدالة في عملية التنقل بالعمق أولًا. فإن وصلنا إلى رأس موجود فعلًا في مكدس التعاود، فهذا يعني أنّ الشجرة تحتوي على دورة. إن الضلع الذي يربط العقدة الحالية بالعقدة الموجودة في مكدس التعاود هو ضلع خلفي.
تنفيذ الخوارزمية
تعرض الأمثلة التالية طريقة تنفيذ هذه الخوارزمية في عدد من لغات البرمجة:
- C++:
#include<iostream>
#include <list>
#include <limits.h>
using namespace std;
class Graph
{
int V; // عدد الرؤوس
list<int> *adj; // مؤشر إلى مصفوفة تحتوي على قوائم المجاورة
bool isCyclicUtil(int v, bool visited[], bool *rs); // isCyclic() تستخدم هذه الدالة من قبل الدالة
public:
Graph(int V); // إنشاء كائن الرسم البياني
void addEdge(int v, int w); // إضافة ضلع إلى الرسم البياني
bool isCyclic(); // تعيد الدالة قيمة صحيحة عند وجود دورة في الرسم البياني
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // إضافة الضلع المعطى
}
bool Graph::isCyclicUtil(int v, bool visited[], bool *recStack)
{
if(visited[v] == false)
{
// تعليم العقدة المعطاة على أنّها مزورة وأنّها في مكدس التعاود
visited[v] = true;
recStack[v] = true;
// تنفيذ الدالة تعاوديًا على جميع الرؤوس المجاورة
list<int>::iterator i;
for(i = adj[v].begin(); i != adj[v].end(); ++i)
{
if ( !visited[*i] && isCyclicUtil(*i, visited, recStack) )
return true;
else if (recStack[*i])
return true;
}
}
recStack[v] = false; // حذف الرأس من مكدس التعاود
return false;
}
// تعيد الدالة قيمة صحيحة إن احتوى الرسم البياني على دورة وإلا فإنّها تعيد قيمة خاطئة
bool Graph::isCyclic()
{
// تعليم العقدة المعطاة على أنّها غير مزورة وأنّها ليست في مكدس التعاود
bool *visited = new bool[V];
bool *recStack = new bool[V];
for(int i = 0; i < V; i++)
{
visited[i] = false;
recStack[i] = false;
}
// استدعاء الدالة التعاودية المساعدة للكشف عن وجود الدورة في أشجار مختلفة
for(int i = 0; i < V; i++)
if (isCyclicUtil(i, visited, recStack))
return true;
return false;
}
int main()
{
// إنشاء الرسم البياني في أعلاه
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
if(g.isCyclic())
cout << "Graph contains cycle";
else
cout << "Graph doesn't contain cycle";
return 0;
}
- بايثون:
from collections import defaultdict
class Graph():
def __init__(self,vertices):
self.graph = defaultdict(list)
self.V = vertices
def addEdge(self,u,v):
self.graph[u].append(v)
def isCyclicUtil(self, v, visited, recStack):
# تعليم العقدة الحالية على أنّها مزورة
# وإضافتها إلى مكدس التعاود
visited[v] = True
recStack[v] = True
# تنفيذ الدالة تعاوديًا على جميع العقد المجاورة
# إن كانت العقدة المجاورة مزورة وموجودة في
# مكدس التعاود فهذا يعني وجود دورة في الرسم البياني
for neighbour in self.graph[v]:
if visited[neighbour] == False:
if self.isCyclicUtil(neighbour, visited, recStack) == True:
return True
elif recStack[neighbour] == True:
return True
# يجب إزالة العقدة من مكدس التعاود
# قبل إنهاء عمل الدالة
recStack[v] = False
return False
# تعيد الدالة قيمة صحيحة في حال وجود دورة في الرسم البياني
def isCyclic(self):
visited = [False] * self.V
recStack = [False] * self.V
for node in range(self.V):
if visited[node] == False:
if self.isCyclicUtil(node,visited,recStack) == True:
return True
return False
g = Graph(4)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
if g.isCyclic() == 1:
print "Graph has a cycle"
else:
print "Graph has no cycle"
- جافا:
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
class Graph {
private final int V;
private final List<List<Integer>> adj;
public Graph(int V)
{
this.V = V;
adj = new ArrayList<>(V);
for (int i = 0; i < V; i++)
adj.add(new LinkedList<>());
}
private boolean isCyclicUtil(int i, boolean[] visited,
boolean[] recStack)
{
// تعليم العقدة الحالية على أنّها مزورة
// وإضافتها إلى مكدس التعاود
if (recStack[i])
return true;
if (visited[i])
return false;
visited[i] = true;
recStack[i] = true;
List<Integer> children = adj.get(i);
for (Integer c: children)
if (isCyclicUtil(c, visited, recStack))
return true;
recStack[i] = false;
return false;
}
private void addEdge(int source, int dest) {
adj.get(source).add(dest);
}
// تعيد الدالة قيمة صحيحة في حال وجود دورة في الرسم البياني
private boolean isCyclic()
{
// تعليم جميع الرؤوس على أنّها غير مزورة
// وأنّها ليست جزءًا من مكدس التعاود
boolean[] visited = new boolean[V];
boolean[] recStack = new boolean[V];
// استدعاء الدالة التعاودية المساعدة للكشف عن وجود الدورة في أشجار مختلفة
for (int i = 0; i < V; i++)
if (isCyclicUtil(i, visited, recStack))
return true;
return false;
}
// اختبار التوابع السابقة
public static void main(String[] args)
{
Graph graph = new Graph(4);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.addEdge(2, 0);
graph.addEdge(2, 3);
graph.addEdge(3, 3);
if(graph.isCyclic())
System.out.println("Graph contains cycle");
else
System.out.println("Graph doesn't "
+ "contain cycle");
}
}
التعقيد الزمني
التعقيد الزمني لهذه العملية مشابه للتعقيد الزمني لعملية البحث بالعمق أولًا وهي O(V+E).
الكشف عن وجود دورة في الرسم البياني غير الموجّه - خوارزمية "وحّد-جد"
المجموعة المفككة disjoint-set هي إحدى بنى المعطيات التي تتابع مجموعة من العناصر المقسّمة إلى عدد من المجاميع الفرعية (غير المتداخلة) المفككة. تجري خوارزمية وحّد-جِدْ union-find عمليتين مفيدتين على المجموعات المفككة، وهما:
- جد Find: تحدّد هذه العملية ما إذا كان عنصر معيّن موجودًا في المجموعة، ويمكن استخدام هذه العملية لمعرفة ما إذا كان عنصران موجودين في المجموعة الفرعية نفسها.
- وحّد: توّحد هذه العملية مجموعتين فرعيتين في مجموعة فرعية واحدة.
يمكن الاستفادة من المجموعات المفككة وخوارزمية وحّد-جِد في الكشف عن وجود دورة في الرسم البياني، وتفترض هذه الطريقة عدم وجود حلقات ذاتية في الرسم البياني.
يمكن متابعة المجموعات الفرعية باستخدام مصفوفة أحادية الأبعاد (ليكن اسمها parent[].
لنأخذ الرسم البياني التالي كمثال:
تصنع الخوارزمية مجاميع فرعية لكلّ ضلع في الرسم البياني وذلك باستخدام رأسي الضلع، فإن عُثر على أنّ الرأسين موجودان في المجموعة الفرعية نفسها، فإن هذا يعني وجود دورة في الرسم البياني.
الخطوة الأولى هي تهيئة جميع المواقع في المصفوفة الأب لتحمل القيمة -1 (وهذا يعني وجود عنصر واحد في كل مجموعة فرعية).
0 1 2
-1 -1 -1
والآن سنعالج الأضلاع واحدًا تلو الآخر.
الضلع 0-1: جد المجاميع الفرعية التي يوجد فيها الرأسان 0 و 1. لمّا كان الرأسان في مجموعتين فرعيتين مختلفتين، فسنأخذ المجموعة الناتجة من اتحاد المجموعتين، وإما أن نجعل العقدة 0 هي العقدة الأم للعقدة 1 أو بالعكس.
الضلع 1-2: الرأس 1 موجود في المجموعة الفرعية 1 و الرأس 2 موجود في المجموعة الفرعية 2؛ لذا سنوحّدهما.
الضلع 0-2: الرأس 0 موجود في المجموعة الفرعية 2 والرأس 2 موجود كذلك في المجموعة الفرعية 2. نستنتج من ذلك أنّ هذا الضلع يشكّل دورة.
تنفيذ الخوارزمية
تعرض الأمثلة التالية طريقة تنفيذ خوارزمية وحّدِ-جِد في عدد من لغات البرمجة.
#include <bits/stdc++.h>
using namespace std;
// تمثيل ضلع في الرسم البياني
class Edge
{
public:
int src, dest;
};
// تمثيل الرسم البياني
class Graph
{
public:
// V-> عدد الرؤوس
// E-> عدد الأضلاع
int V, E;
// يمثل الضلع بهيئة مصفوفة من الأضلاع
Edge* edge;
};
// تنشئ الدالة رسمًاً بيانيًا يتضمّن الرؤوس والأضلاع المعطاة
Graph* createGraph(int V, int E)
{
Graph* graph = new Graph();
graph->V = V;
graph->E = E;
graph->edge = new Edge[graph->E * sizeof(Edge)];
return graph;
}
// دالة مساعدة للعثور على المجموعة الفرعية التي ينتمي إليها العنصر المعطى
int find(int parent[], int i)
{
if (parent[i] == -1)
return i;
return find(parent, parent[i]);
}
// دالة مساعدة لتوحيد مجموعتين فرعيتين
void Union(int parent[], int x, int y)
{
int xset = find(parent, x);
int yset = find(parent, y);
if(xset != yset)
{
parent[xset] = yset;
}
}
// الدالة الرئيسية التي تتحقّق ممّأ إذا كان الرسم البياني المعطى
// يحتوي على دورة أو لا
int isCycle( Graph* graph )
{
// حجز موقع في الذاكرة لإنشاء مجموعات الرؤوس الفرعية
int *parent = new int[graph->V * sizeof(int)];
// تهيئة جميع المجموعات الفرعية لتكون مجموعات ذات عنصر واحد
memset(parent, -1, sizeof(int) * graph->V);
// المرور على جميع الأضلع في الرسم البياني، والعثور على المجموعات الفرعية
// لكلا الرأسين المكونين لكل ضلع، وإذا عُثر على مجموعتين فرعيتين متشابهتين
// فإن هذا يعني أن الرسم البياني يحتوي على دورة
for(int i = 0; i < graph->E; ++i)
{
int x = find(parent, graph->edge[i].src);
int y = find(parent, graph->edge[i].dest);
if (x == y)
return 1;
Union(parent, x, y);
}
return 0;
}
// اختبار الدوال السابقة
int main()
{
/* إنشاء الرسم البياني التالي
0
| \
| \
1-----2 */
int V = 3, E = 3;
Graph* graph = createGraph(V, E);
// إضافة الضلع 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
// إضافة الضلع 1-2
graph->edge[1].src = 1;
graph->edge[1].dest = 2;
// إضافة الضلع 0-2
graph->edge[2].src = 0;
graph->edge[2].dest = 2;
if (isCycle(graph))
cout<<"graph contains cycle";
else
cout<<"graph doesn't contain cycle";
return 0;
}
- بايثون:
# هناك ضلع واحد لأي رأسين في الرسم البياني، بمعنى أنّ الرأسين 1 و 2 يشكّلان الضلع 1-2 أو 2-1 وليس كلاهما
from collections import defaultdict
# يستخدم هذا الصنف لتمثيل الرسم البياني غير الموجّه باستخدام قائمة المجاورة
class Graph:
def __init__(self,vertices):
self.V= vertices # عدد الرؤوس
self.graph = defaultdict(list) # القاموس الافتراضي الذي يستخدم لتخزين الرسم البياني
# دالة لإضافة ضلع إلى الرسم البياني
def addEdge(self,u,v):
self.graph[u].append(v)
# دالة مساعدة للعثور على المجموعة الفرعية التي ينتمي إليها العنصر المعطى
def find_parent(self, parent,i):
if parent[i] == -1:
return i
if parent[i]!= -1:
return self.find_parent(parent,parent[i])
# دالة مساعدة لتوحيد مجموعتين فرعيتين
def union(self,parent,x,y):
x_set = self.find_parent(parent, x)
y_set = self.find_parent(parent, y)
parent[x_set] = y_set
# الدالة الرئيسية التي تتحقق ممّا إذا كان الرسم البياني المعطى
# يحتوي على دورة أم لا
def isCyclic(self):
# حجز موقع في الذاكرة لإنشاء مجموعة الرؤوس الفرعية
# وتهيئة جميع المجموعات الفرعية لتكون مجموعات ذات عنصر واحد
parent = [-1]*(self.V)
# المرور على جميع الأضلع في الرسم البياني، والعثور على المجموعات الفرعية
# لكلا الرأسين المكونين لكل ضلع، وإذا عُثر على مجموعتين فرعيتين متشابهتين
# فإن هذا يعني أن الرسم البياني يحتوي على دورة
for i in self.graph:
for j in self.graph[i]:
x = self.find_parent(parent, i)
y = self.find_parent(parent, j)
if x == y:
return True
self.union(parent,x,y)
# إنشاء الرسم البياني أعلاه
g = Graph(3)
g.addEdge(0, 1)
g.addEdge(1, 2)
g.addEdge(2, 0)
if g.isCyclic():
print "Graph contains cycle"
else :
print "Graph does not contain cycle "
- جافا:
import java.util.*;
import java.lang.*;
import java.io.*;
class Graph
{
// V-> عدد الرؤوس
// E-> عدد الأضلاع
int V, E;
Edge edge[]; // مجموعة الأضلاع
class Edge
{
int src, dest;
};
// إنشاء رسم بياني يتكون من الرؤوس والأضلاع المعطاة
Graph(int v,int e)
{
V = v;
E = e;
edge = new Edge[E];
for (int i=0; i<e; ++i)
edge[i] = new Edge();
}
// دالة مساعدة للعثور على المجموعة الفرعية التي ينتمي إليها العنصر المعطى
int find(int parent[], int i)
{
if (parent[i] == -1)
return i;
return find(parent, parent[i]);
}
// دالة مساعدة لتوحيد مجموعتين فرعيتين
void Union(int parent[], int x, int y)
{
int xset = find(parent, x);
int yset = find(parent, y);
parent[xset] = yset;
}
// الدالة الرئيسية التي تتحقق من أنّ الرسم البياني المعطى
// يحتوي على دورة أو لا
int isCycle( Graph graph)
{
// حجز موقع في الذاكرة لإنشاء مجموعة الرؤوس الفرعية
int parent[] = new int[graph.V];
// تهيئة جميع المجموعات الفرعية لتكون مجموعات ذات عنصر واحد
for (int i=0; i<graph.V; ++i)
parent[i]=-1;
// المرور على جميع الأضلع في الرسم البياني، والعثور على المجموعات الفرعية
// لكلا الرأسين المكونين لكل ضلع، وإذا عُثر على مجموعتين فرعيتين متشابهتين
// فإن هذا يعني أن الرسم البياني يحتوي على دورة
for (int i = 0; i < graph.E; ++i)
{
int x = graph.find(parent, graph.edge[i].src);
int y = graph.find(parent, graph.edge[i].dest);
if (x == y)
return 1;
graph.Union(parent, x, y);
}
return 0;
}
// اختبار الدوال السابقة
public static void main (String[] args)
{
/* إنشاء الرسم البياني التالي
0
| \
| \
1-----2 */
int V = 3, E = 3;
Graph graph = new Graph(V, E);
// إضافة الضلع 0-1
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
// إضافة الضلع 1-2
graph.edge[1].src = 1;
graph.edge[1].dest = 2;
// إضافة الضلع 0-2
graph.edge[2].src = 0;
graph.edge[2].dest = 2;
if (graph.isCycle(graph)==1)
System.out.println( "graph contains cycle" );
else
System.out.println( "graph doesn't contain cycle" );
}
}
مصادر
- صفحة Detect Cycle in a Directed Graph في توثيق الخوارزميات في موقع GeeksforGeeks.
- صفحة Disjoint Set (Or Union-Find) في توثيق الخوارزميات في موقع GeeksforGeeks.