الفرق بين المراجعتين لصفحة: «Algorithms/Kruskal MST»
لا ملخص تعديل |
جميل-بيلوني (نقاش | مساهمات) طلا ملخص تعديل |
||
| (3 مراجعات متوسطة بواسطة مستخدم واحد آخر غير معروضة) | |||
| سطر 1: | سطر 1: | ||
<noinclude>{{DISPLAYTITLE:خوارزمية كروسكال لإيجاد الشجرة الممتدة الصغرى}}</noinclude> | <noinclude>{{DISPLAYTITLE:خوارزمية كروسكال لإيجاد الشجرة الممتدة الصغرى}}</noinclude> | ||
الشجرة الممتدة | تعثر خوارزمية كروسكال Kruskal على الشجرة الممتدة الصغرى في الرسم البياني المعطى، بترتيب الأضلاع تصاعديًا ثم اختيار الضلع الأصغر. | ||
== خطوات عمل الخوارزمية == | |||
يمكن تقسيم عمل خوارزمية كروسكال Kruskal إلى الخطوات التالية: | |||
== خطوات الخوارزمية == | |||
يمكن تقسيم عمل خوارزمية كروسكال Kruskal إلى الخطوات التالية: | |||
# ترتيب جميع الأضلاع بترتيب تصاعدي بالاعتماد على أوزانها. | # ترتيب جميع الأضلاع بترتيب تصاعدي بالاعتماد على أوزانها. | ||
| سطر 238: | سطر 233: | ||
} | } | ||
</source> | </source> | ||
* بايثون: | * [[Python|بايثون]]: | ||
<source lang="python">from collections import defaultdict | <source lang="python">from collections import defaultdict | ||
| سطر 511: | سطر 506: | ||
graph.KruskalMST(); | graph.KruskalMST(); | ||
} | } | ||
} </source> | } </source>تعطي الشيفرات السابقة المخرجات التالية:<syntaxhighlight lang="text"> | ||
Following are the edges in the constructed MST | |||
2 -- 3 == 4 | |||
0 -- 3 == 5 | |||
0 -- 1 == 10 | |||
</syntaxhighlight> | |||
== التعقيد الزمني == | == التعقيد الزمني == | ||
يبلغ التعقيد الزمني لهذه الخوارزمية المقدار <code>O(ElogE)</code> أو <code>O(ElogV)</code>. تستغرق عملية ترتبي الأضلاع المقدار <code>O(ElogE)</code>، وبعد إجراء عملية الترتيب سنمرّ على جميع الأضلاع لتنفيذ خوارزمية وحِّد-جِد. يمكن لعمليتي الإيجاد والتوحيد أن تستغرقا وقتًا قدره <code>O(LogV)</code> في الحد الأقصى؛ لذا فإنّ التعقيد الزمني الكلي يبلغ <code>O(ElogE + ELogV)</code>. القيمة القصوى لـ <code>E</code> هي <code>O(V2)</code>، وهكذا تكون <code>O(LogV)</code> و <code>O(LogE)</code> متساويتين؛ لذا يمكن القول أن التعقيد الزمني لهذه الخوارزمية هو <code>O(ElogE)</code> أو <code>O(ElogV)</code>. | يبلغ التعقيد الزمني لهذه الخوارزمية المقدار <code>O(ElogE)</code> أو <code>O(ElogV)</code>. تستغرق عملية ترتبي الأضلاع المقدار <code>O(ElogE)</code>، وبعد إجراء عملية الترتيب سنمرّ على جميع الأضلاع لتنفيذ خوارزمية وحِّد-جِد. يمكن لعمليتي الإيجاد والتوحيد أن تستغرقا وقتًا قدره <code>O(LogV)</code> في الحد الأقصى؛ لذا فإنّ التعقيد الزمني الكلي يبلغ <code>O(ElogE + ELogV)</code>. القيمة القصوى لـ <code>E</code> هي <code>O(V2)</code>، وهكذا تكون <code>O(LogV)</code> و <code>O(LogE)</code> متساويتين؛ لذا يمكن القول أن التعقيد الزمني لهذه الخوارزمية هو <code>O(ElogE)</code> أو <code>O(ElogV)</code>. | ||
== انظر أيضًا == | |||
* [[Algorithms/Prim MST|خوارزمية برم لإيجاد الشجرة الممتدة الصغرى:]] تعثر خوارزمية برم Prim على الشجرة الممتدة الصغرى في الرسم البياني المعطى، وتبدأ بشجرة ممتدة فارغة وتعتمد في عملها على مجموعتين من الرؤوس. | |||
== مصادر == | == مصادر == | ||
المراجعة الحالية بتاريخ 09:07، 7 أكتوبر 2022
تعثر خوارزمية كروسكال Kruskal على الشجرة الممتدة الصغرى في الرسم البياني المعطى، بترتيب الأضلاع تصاعديًا ثم اختيار الضلع الأصغر.
خطوات عمل الخوارزمية
يمكن تقسيم عمل خوارزمية كروسكال Kruskal إلى الخطوات التالية:
- ترتيب جميع الأضلاع بترتيب تصاعدي بالاعتماد على أوزانها.
- اختيار الضلع الأصغر، ثم التأكد من أنّه يشكّل دائرة مع الشجرة الممتدة الصغرى التي يجري بناؤها، أما في حال عدم تكوين دائرة، فإنّ هذا الضلع سيُضاف إلى الشجرة، وإلا فإنّ الخوارزمية ستتجاهله. تستخدم هذه الخطوة خوارزمية وحّد-جِد Union-Find للكشف عن وجود الدورة في الرسم البياني.
- تكرار الخطوة الثانية إلى أن يصبح عدد الأضلاع
(V-1)في الشجرة الممتدة.
يمكن توضيح الخطوات السابقة بالمثال التالي:
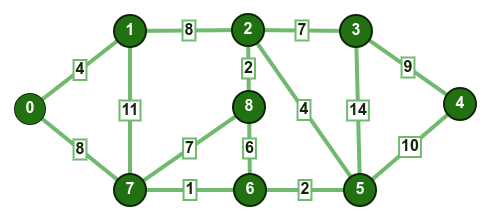
يحتوي الرسم البياني أعلاه على 9 رؤوس و 14 ضلعًا؛ لذا فإنّ الشجرة الممتدة الصغرى التي ستتكون من هذا الرسم البياني ستمتلك (9 - 1) = 8 ضلعًا.
سنبدأ باختيار جميع الأضلاع واحدًا تلو الآخر من قائمة الأضلاع المرتبة:
- نختار الضلع
7-6: لم تتكون أي دائرة، نضيف الضلع إلى الشجرة.
- نختار الضلع
8-2: لم تتكون أي دائرة، نضيف الضلع إلى الشجرة.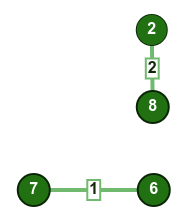
- نختار الضلع
6-5: لم تتكون أي دائرة، نضيف الضلع إلى الشجرة.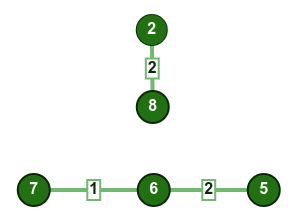
- نختار الضلع
0-1: لم تتكون أي دائرة، نضيف الضلع إلى الشجرة.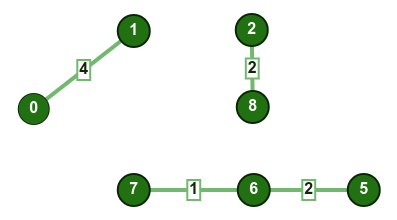
- نختار الضلع
2-5: لم تتكون أي دائرة، نضيف الضلع إلى الشجرة.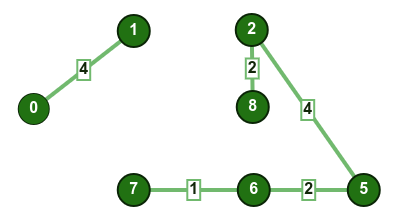
- نختار الضلع
8-6: تؤدي إضافة هذا الضلع إلى إنشاء دورة، لذا سنتجاهله. - نختار الضلع
2-3: لم تتكون أي دائرة، نضيف الضلع إلى الشجرة.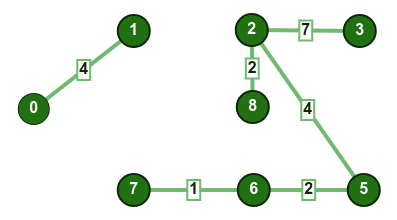
- نختار الضلع
7-8: تؤدي إضافة هذا الضلع إلى إنشاء دورة، لذا سنتجاهله. - نختار الضلع
0-7: لم تتكون أي دائرة، نضيف الضلع إلى الشجرة.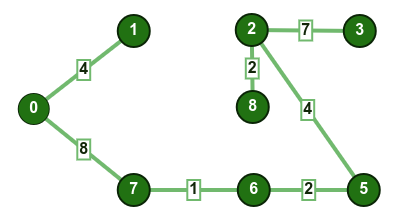
- نختار الضلع
1-2: تؤدي إضافة هذا الضلع إلى إنشاء دورة، لذا سنتجاهله. - نختار الضلع
3-4: لم تتكون أي دائرة، نضيف الضلع إلى الشجرة.
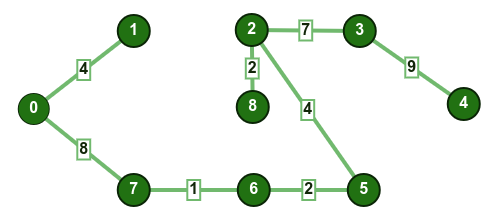
أصبح عدد الأضلاع المضافة مساويًا للقيمة (V - 1)، وستتوقف الخوارزمية عند هذه النقطة.
أسلوب الخوارزمية
خوارزمية كروسكال من الخوارزميات الجشعة، والاختيار الجشع فيها هو انتخاب الضلع ذي الوزن الأصغر والذي لا يشكل دورة في الشجرة الممتدة الصغرى التي يجري بناؤها.
تنفيذ الخوارزمية
تعرض الأمثلة التالية طريقة تنفيذ خوارزمية كروسكال في عدد من لغات البرمجة:
- C++:
#include <bits/stdc++.h>
using namespace std;
// تمثيل الضلع الموزون في الرسم البياني
class Edge
{
public:
int src, dest, weight;
};
// تمثيل الرسم البياني المتصل وغير الموجه والموزون
class Graph
{
public:
// V -> عدد الرؤوس
// E -> عدد الأضلاع
int V, E;
// يمثَّل الرسم البياني كمصفوفة من الأضلاع
// لما كان الرسم البياني غير موجه فإنّ الضلع
// الذي يبدأ من الوجه وينتهي بالهدف يكون في الوقت نفسه
// ضلع يبدأ من الهدف وينتهي بالوجهة.
// ويحسب الضلعان كضلع واحد.
Edge* edge;
};
// إنشاء رسم بياني يحتوي على عدد الرؤوس والأضلاع المعطاة
Graph* createGraph(int V, int E)
{
Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
// تمثيل مجموعة فرعية لخوارزمية وحد-جد
class subset
{
public:
int parent;
int rank;
};
// i دالة مساعدة للعثور على مجموعة العنصر
// (تستخدم طريقة ضغط المسار)
int find(subset subsets[], int i)
{
// i العثور على الجذر وجعله أبًا للعنصر
// (ضغط المسار)
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
// الدالة المسؤولة عن العثور على مجموعتين للعنصرين المعطيين
// (تستخدم طريقة التوحيد بالمرتبة)
void Union(subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// ربط الشجرة ذات الرتبة الأصغر تحت جذر
// الشجرة ذات الرتبة الأكبر (التوحيد بالمرتبة)
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
// إن كانت المراتب متساوية، سنجعل إحدى الشجرتين جذرًا
// ونرفع رتبتها بمقدار واحد
else
{
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// مقارنة الضلعين حسب أوزانهما
// تستخدم لترتيب مصفوفة من الأضلاع
int myComp(const void* a, const void* b)
{
Edge* a1 = (Edge*)a;
Edge* b1 = (Edge*)b;
return a1->weight > b1->weight;
}
// الدالة الرئيسية المسؤولة عن بناء الشجرة الممتدة الصغرى باستخدام خوارزمية كروسكال
void KruskalMST(Graph* graph)
{
int V = graph->V;
Edge result[V]; // هنا ستخزن الشجرة الممتدة الصغرى الناشئة
int e = 0; // result[] متغير للموقع يستخدم مع المصفوفة
int i = 0; // متغير للموقع يستخدم مع الأضلاع المرتبة
// الخطوة الأولى: ترتيب جميع الأضلاع بترتيب تصاعدي
// بالاعتماد على أوزانها. وإن لم يكن بالإمكان تعديل
// الرسم البياني المعطى، يمكن إنشاء نسخة من مصفوفة الأضلاع
qsort(graph->edge, graph->E, sizeof(graph->edge[0]), myComp);
// حجز الذاكرة اللازمة لإنشاء مجموعة الرؤوس الفرعية
subset *subsets = new subset[( V * sizeof(subset) )];
// إنشاء مجموعة الرؤوس الفرعية مع عنصر واحد
for (int v = 0; v < V; ++v)
{
subsets[v].parent = v;
subsets[v].rank = 0;
}
// V-1 عدد الأضلاع التي ستعمل عليها الخوارزمية يساوي
while (e < V - 1 && i < graph->E)
{
// الخطوة الثانية: اختيار الضلع الأصغر ثم زيادة
// متغير الموقع للدورة القادمة
Edge next_edge = graph->edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
// إن لم تؤد إضافة هذا الضلع إلى تكوين دورة
// نضيف الضلع إلى النتيجة ونزيد قيمة متغير الموقع
// لمصفوفة النتيجة وذلك لاستقبال الضلع التالي
if (x != y)
{
result[e++] = next_edge;
Union(subsets, x, y);
}
// وإلا سنتجاهل الضلع التالي
}
// طباعة محتويات مصفوفة النتائج وعرض الشجرة الممتدة الصغرى التي تم بناؤها
cout<<"Following are the edges in the constructed MST\n";
for (i = 0; i < e; ++i)
cout<<result[i].src<<" -- "<<result[i].dest<<" == "<<result[i].weight<<endl;
return;
}
// اختبار الدوال السابقة
int main()
{
/* إنشاء الرسم البياني التالي
10
0--------1
| \ |
6| 5\ |15
| \ |
2--------3
4 */
int V = 4; // عدد الرؤوس في الرسم البياني
int E = 5; // عدد الأضلاع في الرسم البياني
Graph* graph = createGraph(V, E);
// إضافة الضلع 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = 10;
// إضافة الضلع 0-2
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 6;
// إضافة الضلع 0-3
graph->edge[2].src = 0;
graph->edge[2].dest = 3;
graph->edge[2].weight = 5;
// إضافة الضلع 1-3
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 15;
// إضافة الضلع 2-3
graph->edge[4].src = 2;
graph->edge[4].dest = 3;
graph->edge[4].weight = 4;
KruskalMST(graph);
return 0;
}
from collections import defaultdict
# تمثيل الرسم البياني
#Class to represent a graph
class Graph:
def __init__(self,vertices):
self.V= vertices # عدد الرؤوس
self.graph = [] # قاموس افتراضي لتخزين الرسم البياني
# دالة لإضافة ضلع إلى الرسم البياني
def addEdge(self,u,v,w):
self.graph.append([u,v,w])
# i دالة مساعدة للعثور على مجموعة العنصر
# (تستخدم طريقة ضغط المسار)
def find(self, parent, i):
if parent[i] == i:
return i
return self.find(parent, parent[i])
# الدالة المسؤولة عن العثور على مجموعتين للعنصرين المعطيين
# (تستخدم طريقة التوحيد بالمرتبة)
def union(self, parent, rank, x, y):
xroot = self.find(parent, x)
yroot = self.find(parent, y)
# ربط الشجرة ذات الرتبة الأصغر تحت جذر
# ربط الشجرة ذات الرتبة الأصغر تحت جذر
if rank[xroot] < rank[yroot]:
parent[xroot] = yroot
elif rank[xroot] > rank[yroot]:
parent[yroot] = xroot
# إن كانت المراتب متساوية، سنجعل إحدى الشجرتين جذرًا
# ونرفع رتبتها بمقدار واحد
else :
parent[yroot] = xroot
rank[xroot] += 1
# الدالة الرئيسية المسؤولة عن بناء الشجرة الممتدة الصغرى باستخدام خوارزمية كروسكال
def KruskalMST(self):
result =[] #هنا ستخزن الشجرة الممتدة الصغرى
i = 0 # متغير للموقع يستخدم مع الأضلاع المرتبة
e = 0 # result[] متغير للموقع يستخدم مع المصفوفة
# الخطوة الأولى: ترتيب جميع الأضلاع بترتيب تصاعدي
# بالاعتماد على أوزانها. وإن لم يكن بالإمكان تعديل
# الرسم البياني المعطى، يمكن إنشاء نسخة من مصفوفة الأضلاع
self.graph = sorted(self.graph,key=lambda item: item[2])
parent = [] ; rank = []
# إنشاء مجموعة الرؤوس الفرعية مع عنصر واحد
for node in range(self.V):
parent.append(node)
rank.append(0)
# V-1 عدد الأضلاع التي ستعمل عليها الخوارزمية يساوي
while e < self.V -1 :
# الخطوة الثانية: اختيار الضلع الأصغر ثم زيادة
# متغير الموقع للدورة القادمة
u,v,w = self.graph[i]
i = i + 1
x = self.find(parent, u)
y = self.find(parent ,v)
# إن لم تؤد إضافة هذا الضلع إلى تكوين دورة
# نضيف الضلع إلى النتيجة ونزيد قيمة متغير الموقع
# لمصفوفة النتيجة وذلك لاستقبال الضلع التالي
if x != y:
e = e + 1
result.append([u,v,w])
self.union(parent, rank, x, y)
# وإلا سنتجاهل الضلع التالي
# طباعة محتويات مصفوفة النتائج وعرض الشجرة الممتدة الصغرى التي تم بناؤها
print "Following are the edges in the constructed MST"
for u,v,weight in result:
#print str(u) + " -- " + str(v) + " == " + str(weight)
print ("%d -- %d == %d" % (u,v,weight))
# اختبار الدوال السابقة
g = Graph(4)
g.addEdge(0, 1, 10)
g.addEdge(0, 2, 6)
g.addEdge(0, 3, 5)
g.addEdge(1, 3, 15)
g.addEdge(2, 3, 4)
g.KruskalMST()
- جافا
import java.util.*;
import java.lang.*;
import java.io.*;
class Graph
{
// صنف لتمثيل الضلع في الرسم البياني
class Edge implements Comparable<Edge>
{
int src, dest, weight;
// دالة مقارنة تستخدم لترتيب الأضلاع
// بالاعتماد على أوزانها
public int compareTo(Edge compareEdge)
{
return this.weight-compareEdge.weight;
}
};
// صنف يمثّل مجموعة فرعية تستخدم في خوارزمية وحد-جد
class subset
{
int parent, rank;
};
// V -> عدد الرؤوس
// ُE -> عدد الأضلاع
int V, E;
Edge edge[]; // مجموعة تحتوي على جميع الأضلاع
// إنشاء رسم بياني يحتوي على الرؤوس والأضلاع المعطاة
Graph(int v, int e)
{
V = v;
E = e;
edge = new Edge[E];
for (int i=0; i<e; ++i)
edge[i] = new Edge();
}
// i دالة مساعدة للعثور على مجموعة العنصر
// (تستخدم طريقة ضغط المسار)
int find(subset subsets[], int i)
{
// i العثور على الجذر وجعله أبًا للعنصر
// (ضغط المسار)
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
// الدالة المسؤولة عن العثور على مجموعتين للعنصرين المعطيين
// (تستخدم طريقة التوحيد بالمرتبة)
void Union(subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// ربط الشجرة ذات الرتبة الأصغر تحت جذر
// الشجرة ذات الرتبة الأكبر (التوحيد بالمرتبة)
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
// إن كانت المراتب متساوية، سنجعل إحدى الشجرتين جذرًا
// ونرفع رتبتها بمقدار واحد
else
{
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// الدالة الرئيسية المسؤولة عن بناء الشجرة الممتدة الصغرى باستخدام خوارزمية كروسكال
void KruskalMST()
{
Edge result[] = new Edge[V]; // Tهنا ستخزن الشجرة الممتدة الصغرى
int e = 0; // result[] متغير للموقع يستخدم مع المصفوفة
int i = 0; // متغير للموقع يستخدم مع الأضلاع المرتبة
for (i=0; i<V; ++i)
result[i] = new Edge();
// الخطوة الأولى: ترتيب جميع الأضلاع بترتيب تصاعدي
// بالاعتماد على أوزانها. وإن لم يكن بالإمكان تعديل
// الرسم البياني المعطى، يمكن إنشاء نسخة من مصفوفة الأضلاع
Arrays.sort(edge);
// حجز الذاكرة اللازمة لإنشاء مجموعة الرؤوس الفرعية
subset subsets[] = new subset[V];
for(i=0; i<V; ++i)
subsets[i]=new subset();
// إنشاء مجموعة الرؤوس الفرعية مع عنصر واحد
for (int v = 0; v < V; ++v)
{
subsets[v].parent = v;
subsets[v].rank = 0;
}
i = 0; // الفهرس المستخدم لالتقاط الضلع التالي
// V-1 عدد الأضلاع التي ستعمل عليها الخوارزمية يساوي
while (e < V - 1)
{
// الخطوة الثانية: اختيار الضلع الأصغر ثم زيادة
// متغير الموقع للدورة القادمة
Edge next_edge = new Edge();
next_edge = edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
// إن لم تؤد إضافة هذا الضلع إلى تكوين دورة
// نضيف الضلع إلى النتيجة ونزيد قيمة متغير الموقع
// لمصفوفة النتيجة وذلك لاستقبال الضلع التالي
if (x != y)
{
result[e++] = next_edge;
Union(subsets, x, y);
}
// وإلا سنتجاهل الضلع التالي
}
// طباعة محتويات مصفوفة النتائج وعرض الشجرة الممتدة الصغرى التي تم بناؤها
System.out.println("Following are the edges in " +
"the constructed MST");
for (i = 0; i < e; ++i)
System.out.println(result[i].src+" -- " +
result[i].dest+" == " + result[i].weight);
}
// اختبار الدوال السابقة
public static void main (String[] args)
{
/* إنشاء الرسم البياني التالي
10
0--------1
| \ |
6| 5\ |15
| \ |
2--------3
4 */
int V = 4; // عدد الرؤوس في الرسم البياني
int E = 5; // عدد الأضلاع في الرسم البياني
Graph graph = new Graph(V, E);
// إضافة الضلع 0-1
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = 10;
// إضافة الضلع 0-2
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 6;
// إضافة الضلع 0-3
graph.edge[2].src = 0;
graph.edge[2].dest = 3;
graph.edge[2].weight = 5;
// إضافة الضلع 1-3
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 15;
// إضافة الضلع 2-3
graph.edge[4].src = 2;
graph.edge[4].dest = 3;
graph.edge[4].weight = 4;
graph.KruskalMST();
}
}
تعطي الشيفرات السابقة المخرجات التالية:
Following are the edges in the constructed MST
2 -- 3 == 4
0 -- 3 == 5
0 -- 1 == 10
التعقيد الزمني
يبلغ التعقيد الزمني لهذه الخوارزمية المقدار O(ElogE) أو O(ElogV). تستغرق عملية ترتبي الأضلاع المقدار O(ElogE)، وبعد إجراء عملية الترتيب سنمرّ على جميع الأضلاع لتنفيذ خوارزمية وحِّد-جِد. يمكن لعمليتي الإيجاد والتوحيد أن تستغرقا وقتًا قدره O(LogV) في الحد الأقصى؛ لذا فإنّ التعقيد الزمني الكلي يبلغ O(ElogE + ELogV). القيمة القصوى لـ E هي O(V2)، وهكذا تكون O(LogV) و O(LogE) متساويتين؛ لذا يمكن القول أن التعقيد الزمني لهذه الخوارزمية هو O(ElogE) أو O(ElogV).
انظر أيضًا
- خوارزمية برم لإيجاد الشجرة الممتدة الصغرى: تعثر خوارزمية برم Prim على الشجرة الممتدة الصغرى في الرسم البياني المعطى، وتبدأ بشجرة ممتدة فارغة وتعتمد في عملها على مجموعتين من الرؤوس.
مصادر
- صفحة Kruskal’s Minimum Spanning Tree Algorithm في توثيق الخوارزميات في موقع GeeksforGeeks.