الفرق بين المراجعتين لصفحة: «Algorithms/Juggler sequence»
أنشأ الصفحة ب'<noinclude>{{DISPLAYTITLE:متتالية لاعب الخفة}}</noinclude> متتالية لاعبة الخفة Juggler Sequence هي متتالية من الأعداد...' |
لا ملخص تعديل |
||
| سطر 1: | سطر 1: | ||
<noinclude>{{DISPLAYTITLE:متتالية لاعب الخفة}}</noinclude> | <noinclude>{{DISPLAYTITLE:متتالية لاعب الخفة}}</noinclude> | ||
متتالية لاعبة الخفة Juggler Sequence هي متتالية من الأعداد الصحيحة التي يكون فيها العنصر الأول عددًا صحيحًا موجبًا ويُنتج كل رقم فيها بالاعتماد على العلاقة التعاودية التالية والتي تربطه بالعدد الذي يسبقه: | متتالية لاعبة الخفة Juggler Sequence هي متتالية من الأعداد الصحيحة التي يكون فيها العنصر الأول عددًا صحيحًا موجبًا ويُنتج كل رقم فيها بالاعتماد على العلاقة التعاودية التالية والتي تربطه بالعدد الذي يسبقه: | ||
[[ملف:juggler-sequence-realtionship.svg|مركز|393x393بك]] | |||
فعلى سبيل المثال، تضم المتتالية التي تبدأ بالرقم <code>3</code> الأعداد التالية: | فعلى سبيل المثال، تضم المتتالية التي تبدأ بالرقم <code>3</code> الأعداد التالية: | ||
| سطر 12: | سطر 11: | ||
'''ملاحظات''': | '''ملاحظات''': | ||
* يلاحظ من الأمثلة السابقة أنّ الأعداد في | * يلاحظ من الأمثلة السابقة أنّ الأعداد في متتالية لاعب الخفة تبدأ بالصعود تدريجيًا لتصل إلى قيمة عظمى معينة ثم تبدأ بعدها بالتناقص تدريجيًا. | ||
* تنتهي متتالية لاعب الخفة بالعدد <code>1</code> دائمًا. | * تنتهي متتالية لاعب الخفة بالعدد <code>1</code> دائمًا. | ||
المراجعة الحالية بتاريخ 12:23، 11 أكتوبر 2019
متتالية لاعبة الخفة Juggler Sequence هي متتالية من الأعداد الصحيحة التي يكون فيها العنصر الأول عددًا صحيحًا موجبًا ويُنتج كل رقم فيها بالاعتماد على العلاقة التعاودية التالية والتي تربطه بالعدد الذي يسبقه:
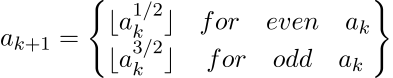
فعلى سبيل المثال، تضم المتتالية التي تبدأ بالرقم 3 الأعداد التالية:
3, 5, 11, 36, 6, 2, 1
فعلى سبيل المثال، تضم المتتالية التي تبدأ بالرقم 9 الأعداد التالية:
9, 27, 140, 11, 36, 6, 2, 1
ملاحظات:
- يلاحظ من الأمثلة السابقة أنّ الأعداد في متتالية لاعب الخفة تبدأ بالصعود تدريجيًا لتصل إلى قيمة عظمى معينة ثم تبدأ بعدها بالتناقص تدريجيًا.
- تنتهي متتالية لاعب الخفة بالعدد
1دائمًا.
تنفيذ الخوارزمية
تعرض الأمثلة التالية طريقة تنفيذ الخوارزمية في عدد من لغات البرمجة:
- C++:
#include<stdio.h>
#include<math.h>
void printJuggler(int n)
{
int a = n;
// طباعة العنصر الأول
printf("%d ", a);
// حساب بقية العناصر ما دام العنصر الأخير لا يساوي 1
while (a != 1)
{
int b = 0;
// التحقق من كون العنصر السابق زوجيًا أو فرديًا
if (a%2 == 0)
// حساب العنصر التالي
b = floor(sqrt(a));
else
// إن كان العنصر السابق فرديًا
b = floor(sqrt(a)*sqrt(a)*sqrt(a));
printf("%d ", b);
a = b;
}
}
//اختبار الدال السابقة
int main()
{
printJuggler(3);
printf("\n");
printJuggler(9);
return 0;
}
- بايثون:
import math
def printJuggler(n) :
a = n
# طباعة العنصر الأول
print a,
# حساب العناصر ما دام العنصر الأخير لا يساوي 1
while (a != 1) :
b = 0
# التحقق من كون العنصر الأول زوجيًا أو فرديًا
if (a%2 == 0) :
# حساب العنصر التالي
b = (int)(math.floor(math.sqrt(a)))
else :
# إن كان العنصر السابق فرديًا
b = (int) (math.floor(math.sqrt(a)*math.sqrt(a)*
math.sqrt(a)))
print b,
a = b
printJuggler(3)
print
printJuggler(9)
- جافا:
import java.io.*;
import java.math.*;
class GFG {
static void printJuggler(int n)
{
int a = n;
// طباعة العنصر الأول
System.out.print(a+" ");
// حساب العناصر ما دام العنصر الأخير لا يساوي 1
while (a != 1)
{
int b = 0;
// التحقق من كون العنصر السابق زوجيًا أو فرديًا
if (a%2 == 0)
// حساب العنصر التالي
b = (int)Math.floor(Math.sqrt(a));
else
// إن كان العنصر السابق فرديًا
b =(int) Math.floor(Math.sqrt(a) *
Math.sqrt(a) * Math.sqrt(a));
System.out.print( b+" ");
a = b;
}
}
// اختبار التابع السابق
public static void main (String[] args) {
printJuggler(3);
System.out.println();
printJuggler(9);
}
}
تعطي الشيفرة السابقة المخرجات التالية:
3 5 11 36 6 2 1
9 27 140 11 36 6 2 1
مصادر
- صفحة Juggler Sequence في توثيق الخوارزميات في موقع GeeksforGeeks.