Algorithms/closest pair of points

تعثر هذه الخوارزمية على أقرب زوج من النقاط في مصفوفة تتكون من عدد معين n من النقاط في مستوى معين، ولهذه الخوارزمية تطبيقات عديدة، فعلى سبيل المثال تستخدم هذه الخوارزمية في أنظمة التحكم بالملاحة الجوية، إذ يكون المطلوب متابعة الطائرات التي تقترب من بعضها البعض والذي يعدّ مؤشرًا على احتمال حدوث التصادم بين طائرتين.

يمكن حساب المسافة بين نقطتين p و q باستخدام العلاقة الرياضية التالية:

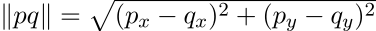
يقدّم أسلوب القوة الغاشمة Brute Force حلّاً لهذه المسألة بتعقيد زمني قدره O(n^2)‎، وذلك بحساب المسافة التي تفصل بين كل زوج من النقاط وإعادة المسافة الأقصر.

يمكن تحسين التعقيد الزمني لهذه المسألة إلى المقدار O(n(Logn)^2)‎ باستخدام أسلوب فرِّق تسد.

خطوات الخوارزمية

تُرتّب عناصر المصفوفة المدخلة قبل البدء بتنفيذ خطوات الخوارزمية بالاعتماد على الإحداثي السيني (x).

1. تحدّد النقطة الوسطى في المصفوفة المرتبة، ويمكن أخذ العنصر P[n/2]‎ كنقطة وسطى.
2. تقسّم المصفوفة المعطاة إلى نصفين. يتضمّن النصف الأول مجموعة النقاط P[0]‎ إلى P[n/2]‎. أما النصف الثاني فيتضمن مجموعة النقاط P[n/2+1]‎ إلى P[n-1]‎.
3. إيجاد المسافات الأقصر في كلتا المصفوفتين الفرعيتين بطريقة تعاودية. نفترض أنّ المسافات هي dl (للنصف الأيسر) و dr (للنصف الأيمن)، وأنّ المسافة الأقصر هي d.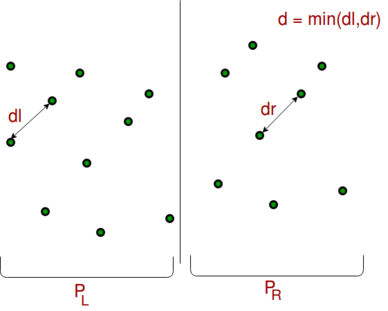

   

4. سنحصل من الخطوات الثلاثة السابقة على الحد العلوي upper bound لقيمة المسافة الأدنى d. سننظر بعد ذلك في أزواج النقاط بحثًا عن زوج يتضمن نقطة تكون في النصف الأيسر وأخرى في النصف الأيمن. سنفترض وجود خط عمودي يمرّ عبر النقطة P[n/2]‎ وسنبحث عن جميع النقاط التي يكون الإحداثي السيني لها أقرب من d إلى الخط العمودي الوسطي، وسننشئ مصفوفة (لتكن strip[]‎) تتضمن جميع هذه النقاط.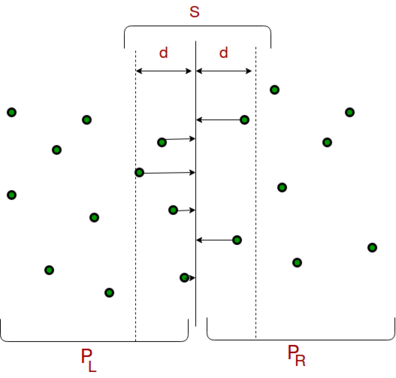

   

5. تُرتّب المصفوفة strip[]‎ بالاعتماد على المحور الصادي (y). يبلغ التعقيد الزمني لهذه الخطوة المقدار O(nLogn)‎، ويمكن تحسينه إلى المقدار O(n)‎ بتنفيذ عمليات الترتيب والدمج بطريقة تعاودية.
6. إيجاد المسافات الأقصر في المصفوفة strip[]‎، وتنفّذ هذه الخطوة بتعقيد زمني قدره O(n)‎.
7. تعيد الخوارزمية في النهاية المسافة الأقصر d والمسافة المحسوبة في الخطوة السادسة.

تنفيذ الخوارزمية

يعرض المثال التالي طريقة تنفيذ الخوارزمية في لغة C++‎‎‎:

#include <bits/stdc++.h> 
using namespace std; 

// تستخدم هذه البنية لتمثيل نقطة في المستوى ثنائي الأبعاد
class Point 
{ 
	public: 
	int x, y; 
}; 

// ترتب الدالة نقاط المصفوفة بالاعتماد على المحور السيني
int compareX(const void* a, const void* b) 
{ 
	Point *p1 = (Point *)a, *p2 = (Point *)b; 
	return (p1->x - p2->x); 
} 
// ترتب الدالة نقاط المصفوفة بالاعتماد على المحور الصادي
int compareY(const void* a, const void* b) 
{ 
	Point *p1 = (Point *)a, *p2 = (Point *)b; 
	return (p1->y - p2->y); 
} 

// دالة مساعدة لإيجاد المسافة بين نقطتين
float dist(Point p1, Point p2) 
{ 
	return sqrt( (p1.x - p2.x)*(p1.x - p2.x) + 
				(p1.y - p2.y)*(p1.y - p2.y) 
			); 
} 

// تستخدم هذه الدالة أسلوب القوة الغاشمة 
// لإعادة أقصر مسافة بين نقطتين في المصفوفة المعطاة ذات الحجم المعطى
float bruteForce(Point P[], int n) 
{ 
	float min = FLT_MAX; 
	for (int i = 0; i < n; ++i) 
		for (int j = i+1; j < n; ++j) 
			if (dist(P[i], P[j]) < min) 
				min = dist(P[i], P[j]); 
	return min; 
} 

// دالة مساعدة للعثور على القيمى الصغرى بين قيمتين عشريتين
float min(float x, float y) 
{ 
	return (x < y)? x : y; 
} 

/* دالة مساعدة للعثور على المسافة الأقصر بين نقطتين 
strip[] جميع النقاط في المصفوفة 
مرتبة بالاعتماد على المحور الصادي، وتمتلك جميع النقاط
d حدًّا أعلى للمسافة الأقصر
O(n^2) قد يُعتقد بأن التعقيد الزمني لهذه الطريقة يبلغ المقدار
O(n) ولكنّه في الواقع
وذلك لأن الحلقة التكرارية الداخلية تتوقف عند الدورة السادسة على الأكثر */
float stripClosest(Point strip[], int size, float d) 
{ 
	float min = d; // تهيئة المسافة الأقصر

	qsort(strip, size, sizeof(Point), compareY); 

	// اختيار النقاط واحدة تلو الأخرى وتجربة النقطة التالية
	// d إلى أن يصبح الفرق بين قيم الإحداثيات الصادية أصغر من المسافة الأقصر
	for (int i = 0; i < size; ++i) 
		for (int j = i+1; j < size && (strip[j].y - strip[i].y) < min; ++j) 
			if (dist(strip[i],strip[j]) < min) 
				min = dist(strip[i], strip[j]); 

	return min; 
} 

// دالة تعاودية لإيجاد المسافة الأقصر.
// المصفوفة المعطاة تحتوي على جميع النقاط
// مرتبة بالاعتماد على المحور السيني
float closestUtil(Point P[], int n) 
{ 
	// إن احتوت المصفوفة المعطاة على نقطتين أو ثلاثة فسنستخدم أسلوب القوة الغاشمة
	if (n <= 3) 
		return bruteForce(P, n); 

	// نبحث عن النقطة الوسطى
	int mid = n/2; 
	Point midPoint = P[mid]; 

	// سنفترض وجود خط عمودي يمر عبر النقطة الوسطى
	// dl تحسب المسافة الأقصر من جهة اليسار
	// dr والمسافة الأقصر من جهة اليمين
	float dl = closestUtil(P, mid); 
	float dr = closestUtil(P + mid, n - mid); 

	// نختار المسافة الأقصر بين المسافتين
	float d = min(dl, dr); 

	// strip[] سننشئ المصفوفة
	// والتي تحتوي على نقاط قريبة من الخط الذي يمر
	// عبر النقطة الوسطية (أقرب من المسافة الأقصر)
	Point strip[n]; 
	int j = 0; 
	for (int i = 0; i < n; i++) 
		if (abs(P[i].x - midPoint.x) < d) 
			strip[j] = P[i], j++; 

	// نختار النقاط الأقرب في المصفوفة
	// d ونعيد القيمة الأصغر بين قيمتي
	// والمسافة الأقصر
	return min(d, stripClosest(strip, j, d) ); 
} 

// الدالة الرئيسية التي تبحث عن المسافة الأقصر
// تعتمد هذه الدالة على الدالة السابقة
float closest(Point P[], int n) 
{ 
	qsort(P, n, sizeof(Point), compareX); 

	// استخدام الدالة السابقة تعاوديًا
	// للعثور على المسافة الأقصر
	return closestUtil(P, n); 
} 

// اختبار الدوال السابقة 
int main() 
{ 
	Point P[] = {{2, 3}, {12, 30}, {40, 50}, {5, 1}, {12, 10}, {3, 4}}; 
	int n = sizeof(P) / sizeof(P[0]); 
	cout << "The smallest distance is " << closest(P, n); 
	return 0; 
}

تعيد الشيفرة السابقة المخرجات التالية:

The smallest distance is 1.414214

ملاحظة:

تستخدم الطريقة أعلاه خوارزمية الترتيب السريع Quick Sort والتي يبلغ تعقيدها الزمني في أسوأ الحالات المقدار O(n^2)‎. يمكن تحسين ذلك باستخدام خوارزميات ترتيب ذات تعقيد زمني O(nLogn)‎ مثل الترتيب بالدمج Merge Sort أو الترتيب بالكومة Heap Sort.

مصادر

• صفحة Closest Pair of Points using Divide and Conquer algorithm في توثيق الخوارزميات في موقع GeeksforGeeks.