الفرق بين المراجعتين لصفحة: «Algorithms/Prim MST»
أنشأ الصفحة ب'<noinclude>{{DISPLAYTITLE:خوارزمية برم لإيجاد الشجرة الممتدة الصغرى}}</noinclude> تبدأ هذه الخوارزمية بشجرة م...' |
|||
| (2 مراجعات متوسطة بواسطة نفس المستخدم غير معروضة) | |||
| سطر 20: | سطر 20: | ||
يوضّح المثال التالي خطوات عمل الخوارزمية: | يوضّح المثال التالي خطوات عمل الخوارزمية: | ||
[[ملف:eg graph.png|وصلة=https://wiki.hsoub.com/%D9%85%D9%84%D9%81:eg%20graph.png|مركز]] | |||
تكون المجموعة <code>mstSet</code> فارغة في البداية والمفاتيح المسندة إلى الرؤوس هي <code>{0, INF, INF, INF, INF, INF, INF, INF}</code> (تمثل <code>INF</code> اللانهاية). نختار الرأس الذي يمتلك أقل قيمة مفتاحية، -وهو في هذه الحالة الرأس <code>0</code>- ونضيفه إلى مجموعة <code>mstSet</code>، فتصبح المجموعة <code>{0}</code>، وبعدها نحدث القيم المفتاحية للرؤوس المجاورة وهما الرأسان <code>1</code> و <code>7</code> إلى القيم <code>4</code> و <code>8</code>. يعرض الرسم البياني التالي الرؤوس التي تم العمل عليها والقيم المفتاحية الخاصة بها، ويعرض الرسم البياني الرؤوس التي تمتلك قيمة محددة فقط، وتحمل الرؤوس المضافة إلى الشجرة الممتدة الصغرى اللون | تكون المجموعة <code>mstSet</code> فارغة في البداية والمفاتيح المسندة إلى الرؤوس هي <code>{0, INF, INF, INF, INF, INF, INF, INF}</code> (تمثل <code>INF</code> اللانهاية). نختار الرأس الذي يمتلك أقل قيمة مفتاحية، -وهو في هذه الحالة الرأس <code>0</code>- ونضيفه إلى مجموعة <code>mstSet</code>، فتصبح المجموعة <code>{0}</code>، وبعدها نحدث القيم المفتاحية للرؤوس المجاورة وهما الرأسان <code>1</code> و <code>7</code> إلى القيم <code>4</code> و <code>8</code>. يعرض الرسم البياني التالي الرؤوس التي تم العمل عليها والقيم المفتاحية الخاصة بها، ويعرض الرسم البياني الرؤوس التي تمتلك قيمة محددة فقط، وتحمل الرؤوس المضافة إلى الشجرة الممتدة الصغرى اللون الأحمر. | ||
[[ملف:prim1.png|مركز]] | |||
نختار الرأس الذي يمتلك القيمة المفتاحية الأقل بشرط أن لا يكون موجودًا في المجموعة <code>mstSet</code>. في هذه الحالة سنختار الرأس <code>1</code> ونضيفه إلى المجموعة <code>mstSet</code> لتصبح بالنتيجة <code>{0, 1}</code>. نحدث بعد ذلك القيمة المفتاحية للرؤوس المجاورة للرأس <code>1</code>، وبذلك تحدّث القيمة المفتاحية للرأس <code>2</code> إلى القيمة <code>8</code>. | نختار الرأس الذي يمتلك القيمة المفتاحية الأقل بشرط أن لا يكون موجودًا في المجموعة <code>mstSet</code>. في هذه الحالة سنختار الرأس <code>1</code> ونضيفه إلى المجموعة <code>mstSet</code> لتصبح بالنتيجة <code>{0, 1}</code>. نحدث بعد ذلك القيمة المفتاحية للرؤوس المجاورة للرأس <code>1</code>، وبذلك تحدّث القيمة المفتاحية للرأس <code>2</code> إلى القيمة <code>8</code>. | ||
[[ملف:prim2.png|مركز|285x285بك]] | |||
نختار الرأس الذي يمتلك القيمة المفتاحية الأقل بشرط أن لا يكون موجودًا في المجموعة <code>mstSet</code>. في هذه الحالة يمكن اختيار أحد الرأسين <code>7</code> أو <code>2</code>، وسنفترض أن الاختيار قد وقع على الرأس <code>7</code>، لذا ستصبح المجموعة <code>mstSet</code> الآن <code>{0, 1, 7}</code>. نحدّث بعد ذلك القيمة المفتاحية للرؤوس المجاورة للرأس <code>7</code>، وبذلك تحدّث القيمة المفتاحية للرأسين <code>6</code> و <code>8</code> إلى القيمتين <code>1</code> و <code>7</code> على التوالي. | نختار الرأس الذي يمتلك القيمة المفتاحية الأقل بشرط أن لا يكون موجودًا في المجموعة <code>mstSet</code>. في هذه الحالة يمكن اختيار أحد الرأسين <code>7</code> أو <code>2</code>، وسنفترض أن الاختيار قد وقع على الرأس <code>7</code>، لذا ستصبح المجموعة <code>mstSet</code> الآن <code>{0, 1, 7}</code>. نحدّث بعد ذلك القيمة المفتاحية للرؤوس المجاورة للرأس <code>7</code>، وبذلك تحدّث القيمة المفتاحية للرأسين <code>6</code> و <code>8</code> إلى القيمتين <code>1</code> و <code>7</code> على التوالي. | ||
[[ملف:prim3.png|مركز]] | |||
نختار الرأس الذي يمتلك القيمة المفتاحية الأقل بشرط أن لا يكون موجودًا في المجموعة <code>mstSet</code>. في هذه الحالة سنختار الرأس <code>6</code> ونضيفه إلى المجموعة <code>mstSet</code> لتصبح بالنتيجة <code>{0, 1, 7, 6}</code>. نحدث بعد ذلك القيمة المفتاحية للرؤوس المجاورة للرأس <code>6</code>، وبذلك تحدّث القيمة المفتاحية للرأسين <code>5</code> و <code>8</code>. | نختار الرأس الذي يمتلك القيمة المفتاحية الأقل بشرط أن لا يكون موجودًا في المجموعة <code>mstSet</code>. في هذه الحالة سنختار الرأس <code>6</code> ونضيفه إلى المجموعة <code>mstSet</code> لتصبح بالنتيجة <code>{0, 1, 7, 6}</code>. نحدث بعد ذلك القيمة المفتاحية للرؤوس المجاورة للرأس <code>6</code>، وبذلك تحدّث القيمة المفتاحية للرأسين <code>5</code> و <code>8</code>. | ||
[[ملف:prim4.png|مركز]] | |||
تكرّر الخطوات السابقة إلى حين دخول جميع الرؤوس في مجموعة <code>mstSet</code>؛ وفي النهاية سنحصل على الرسم البياني التالي: | تكرّر الخطوات السابقة إلى حين دخول جميع الرؤوس في مجموعة <code>mstSet</code>؛ وفي النهاية سنحصل على الرسم البياني التالي: | ||
[[ملف:prim5.png|مركز]] | |||
== تنفيذ الخوارزمية == | == تنفيذ الخوارزمية == | ||
| سطر 39: | سطر 44: | ||
تعرض الأمثلة التالية طريقة تنفيذ الخوارزمية في عدد من لغات البرمجة: | تعرض الأمثلة التالية طريقة تنفيذ الخوارزمية في عدد من لغات البرمجة: | ||
* C++: | * C++: | ||
<source lang="c++">#include <bits/stdc++.h> | <source lang="c++">#include <bits/stdc++.h> | ||
| سطر 338: | سطر 343: | ||
== تنفيذ الخوارزمية على الرسوم البيانية الممثلة بواسطة قائمة المجاورة == | == تنفيذ الخوارزمية على الرسوم البيانية الممثلة بواسطة قائمة المجاورة == | ||
في حال استخدام قوائم المجاورة لتمثيل الرسم البياني، فإن بالإمكان المرور على جميع الرؤوس في الرسم البياني بتعقيد زمني قدره <code>O(V+E)</code> وذلك باستخدام خوارزمية البحث بالعرض أولًا Breadth first search. يتلخص عمل الخوارزمية بهذه الطريقة في المرور على جميع الرؤوس في الرسم البياني باستخدام خوارزمية البحث بالعرض أولًا واستخدام كومة صغرى Min Heap لتخزين الرؤوس غير المضافة بعد إلى الشجرة الممتدة الصغرى. تستخدم الكومة الصغرى كرتل أولوية | في حال استخدام قوائم المجاورة لتمثيل الرسم البياني، فإن بالإمكان المرور على جميع الرؤوس في الرسم البياني بتعقيد زمني قدره <code>O(V+E)</code> وذلك باستخدام خوارزمية [[Algorithms/graphs#.D8.A7.D9.84.D8.AA.D9.86.D9.82.D9.84 .D8.A8.D8.A7.D9.84.D8.B9.D8.B1.D8.B6 .D8.A3.D9.88.D9.84.D9.8B.D8.A7 .D9.81.D9.8A .D8.A7.D9.84.D8.B1.D8.B3.D9.88.D9.85 .D8.A7.D9.84.D8.A8.D9.8A.D8.A7.D9.86.D9.8A.D8.A9|البحث بالعرض أولًا Breadth first search]]. يتلخص عمل الخوارزمية بهذه الطريقة في المرور على جميع الرؤوس في الرسم البياني باستخدام خوارزمية [[Algorithms/graphs#.D8.A7.D9.84.D8.AA.D9.86.D9.82.D9.84 .D8.A8.D8.A7.D9.84.D8.B9.D8.B1.D8.B6 .D8.A3.D9.88.D9.84.D9.8B.D8.A7 .D9.81.D9.8A .D8.A7.D9.84.D8.B1.D8.B3.D9.88.D9.85 .D8.A7.D9.84.D8.A8.D9.8A.D8.A7.D9.86.D9.8A.D8.A9|البحث بالعرض أولًا]] واستخدام [[Algorithms/heaps|كومة صغرى Min Heap]] لتخزين الرؤوس غير المضافة بعد إلى الشجرة الممتدة الصغرى. تستخدم [[Algorithms/heaps|الكومة الصغرى]] [[Algorithms/priority queues|كرتل أولوية priority queue]] للحصول على الضلع الذي يمتلك أقل وزن في المقطع. إن سبب استخدام الكومة الصغرى هو أنّ التعقيد الزمني لعمليات مثل استخراج العنصر الأصغر وإنقاص القيمة المفتاحية تبلغ فيها المقدار <code>O(LogV)</code>. | ||
ويمكن تقسيم عمل الخوارزمية إلى الخطوات التالية: | ويمكن تقسيم عمل الخوارزمية إلى الخطوات التالية: | ||
| سطر 348: | سطر 353: | ||
## لكل عقدة <code>v</code> مجاورة للعقدة <code>u</code>، نتحقّق من أنّ <code>v</code> موجودة في الكومة الصغرى (ليست مضافة بعد إلى الشجرة الممتدة الصغرى). إن كانت <code>v</code> موجود في الكومة الصغرى وكانت قيمتها المفتاحية أكبر من وزن الضلع <code>u-v</code>، فسنحدث القيمة المفتاحية للعقدة <code>v</code> لتكون مساوية لوزن الضلع <code>u-v</code>. | ## لكل عقدة <code>v</code> مجاورة للعقدة <code>u</code>، نتحقّق من أنّ <code>v</code> موجودة في الكومة الصغرى (ليست مضافة بعد إلى الشجرة الممتدة الصغرى). إن كانت <code>v</code> موجود في الكومة الصغرى وكانت قيمتها المفتاحية أكبر من وزن الضلع <code>u-v</code>، فسنحدث القيمة المفتاحية للعقدة <code>v</code> لتكون مساوية لوزن الضلع <code>u-v</code>. | ||
يمكن توضيح الخطوات السابقة بالمثال التالي: | يمكن توضيح الخطوات السابقة بالمثال التالي:[[ملف:eg graph.png|وصلة=https://wiki.hsoub.com/%D9%85%D9%84%D9%81:eg%20graph.png|مركز]] | ||
في البداية، تعطى القيمة المفتاحية <code>0</code> للرأس الأول والقيمة <code>INF</code> (ما لا نهاية) لبقية الرؤوس. يُستخرج الرأس <code>0</code> من الكومة الصغرى وتحدث القيمة المفتاحية للرؤوس المجاورة له (وهما الرأسان <code>1</code> و <code>7</code>). تحتوي الكومة الصغرى على جميع الرؤوس باستثناء الرأس <code>0</code>. | في البداية، تعطى القيمة المفتاحية <code>0</code> للرأس الأول والقيمة <code>INF</code> (ما لا نهاية) لبقية الرؤوس. يُستخرج الرأس <code>0</code> من الكومة الصغرى وتحدث القيمة المفتاحية للرؤوس المجاورة له (وهما الرأسان <code>1</code> و <code>7</code>). تحتوي الكومة الصغرى على جميع الرؤوس باستثناء الرأس <code>0</code>. | ||
الرؤوس الملونة باللون | الرؤوس الملونة باللون الأحمر هي الرؤوس المضافة إلى الشجرة الممتدة الصغرى.[[ملف:prim1.png|مركز]] | ||
لما كانت القيمة المفتاحية للرأس <code>1</code> هي أصغر قيمة بين جميع العقد في الكومة الصغرى، تستخرج الخوارزمية هذه القيمة من الكومة الصغرى وتحدث القيمة المفتاحية للرؤوس المجاورة للرأس <code>1</code> (تحدث القيمة المفتاحية للرأس إذا لم يكن في الكومة الصغرى وكانت القيمة المفتاحية السابقة أكبر من وزن الضلع الذي يربط الرأس <code>1</code> بالرأس المجاور له). تحتوي الكومة الصغرى على جميع الرؤوس باستثناء الرأسين <code>0</code> و <code>1</code>. | لما كانت القيمة المفتاحية للرأس <code>1</code> هي أصغر قيمة بين جميع العقد في الكومة الصغرى، تستخرج الخوارزمية هذه القيمة من الكومة الصغرى وتحدث القيمة المفتاحية للرؤوس المجاورة للرأس <code>1</code> (تحدث القيمة المفتاحية للرأس إذا لم يكن في الكومة الصغرى وكانت القيمة المفتاحية السابقة أكبر من وزن الضلع الذي يربط الرأس <code>1</code> بالرأس المجاور له). تحتوي الكومة الصغرى على جميع الرؤوس باستثناء الرأسين <code>0</code> و <code>1</code>.[[ملف:prim2.png|مركز|285x285بك]] | ||
لما كانت القيمة المفتاحية للرأس <code>7</code> هي أصغر قيمة بين جميع العقد في الكومة الصغرى، تستخرج الخوارزمية هذه القيمة من الكومة الصغرى وتحدث القيمة المفتاحية للرؤوس المجاورة للرأس <code>7</code> (تحدث القيمة المفتاحية للرأس إذا لم يكن في الكومة الصغرى وكانت القيمة المفتاحية السابقة أكبر من وزن الضلع الذي يربط الرأس <code>7</code> بالرأس المجاور له). تحتوي الكومة الصغرى على جميع الرؤوس باستثناء الرؤوس <code>0</code> و <code>1</code> و <code>7</code>. | لما كانت القيمة المفتاحية للرأس <code>7</code> هي أصغر قيمة بين جميع العقد في الكومة الصغرى، تستخرج الخوارزمية هذه القيمة من الكومة الصغرى وتحدث القيمة المفتاحية للرؤوس المجاورة للرأس <code>7</code> (تحدث القيمة المفتاحية للرأس إذا لم يكن في الكومة الصغرى وكانت القيمة المفتاحية السابقة أكبر من وزن الضلع الذي يربط الرأس <code>7</code> بالرأس المجاور له). تحتوي الكومة الصغرى على جميع الرؤوس باستثناء الرؤوس <code>0</code> و <code>1</code> و <code>7</code>.[[ملف:prim3.png|مركز]] | ||
لما كانت القيمة المفتاحية للرأس <code>1</code> هي أصغر قيمة بين جميع العقد في الكومة الصغرى، تستخرج الخوارزمية هذه القيمة من الكومة الصغرى وتحدث القيمة المفتاحية للرؤوس المجاورة للرأس <code>6</code> (تحدث القيمة المفتاحية للرأس إذا لم يكن في الكومة الصغرى وكانت القيمة المفتاحية السابقة أكبر من وزن الضلع الذي يربط الرأس <code>6</code> بالرأس المجاور له). تحتوي الكومة الصغرى على جميع الرؤوس باستثناء الرؤوس <code>0</code> و <code>1</code> و <code>7</code> و <code>6</code>. | لما كانت القيمة المفتاحية للرأس <code>1</code> هي أصغر قيمة بين جميع العقد في الكومة الصغرى، تستخرج الخوارزمية هذه القيمة من الكومة الصغرى وتحدث القيمة المفتاحية للرؤوس المجاورة للرأس <code>6</code> (تحدث القيمة المفتاحية للرأس إذا لم يكن في الكومة الصغرى وكانت القيمة المفتاحية السابقة أكبر من وزن الضلع الذي يربط الرأس <code>6</code> بالرأس المجاور له). تحتوي الكومة الصغرى على جميع الرؤوس باستثناء الرؤوس <code>0</code> و <code>1</code> و <code>7</code> و <code>6</code>.[[ملف:prim4.png|مركز]] | ||
تكرّر الخطوات السابقة على جميع العقد في الكومة الصغرى إلى أن تصبح فارغة. | تكرّر الخطوات السابقة على جميع العقد في الكومة الصغرى إلى أن تصبح فارغة.[[ملف:prim5.png|مركز]] | ||
== أمثلة == | == أمثلة == | ||
تعرض الأمثلة التالية طريقة تنفيذ خوارزمية برم على الرسوم البيانية الممثلة بواسطة قائمة المجاورة: | |||
* C++: | * C++: | ||
<source lang="c++">#include <limits.h> | <source lang="c++">#include <limits.h> | ||
| سطر 881: | سطر 886: | ||
'''ملاحظة''': | '''ملاحظة''': | ||
تستخدم هذه الشيفرة كائن TreeSet عوضًا عن رتل الأولوية PriorityQueue وذلك لأنّ دالة الحذف في رتل الأولوية تعمل بتعقيد زمني قدره <code>O(n)</code> في جافا. | تستخدم هذه الشيفرة كائن <code>TreeSet</code> عوضًا عن رتل الأولوية <code>PriorityQueue</code> وذلك لأنّ دالة الحذف في رتل الأولوية تعمل بتعقيد زمني قدره <code>O(n)</code> في لغة جافا. | ||
<source lang="java">import java.util.LinkedList; | <source lang="java">import java.util.LinkedList; | ||
| سطر 1٬064: | سطر 1٬069: | ||
يمكن تخفيض التعقيد الزمني لهذه الخوارزمية إلى المقدار <code>O(ELogV)</code> باستخدام قائمة المجاورة لتمثيل الرسم البياني. تنفّذ العبارات البرمجية في حلقتي <code>while</code> التكراريتين بتعقيد زمني قدره <code>O(V+E)</code> (تشبه خوارزمية البحث بالعرض أولًا). وتتضمن الحلقة الداخلية العملية <code>decreaseKey()</code> والتي تستغرق <code>O(LogV)</code> من الوقت؛ لذا فإنّ التعقيد الزمني الكلي هو <code>O(E+V) * O(LogV)</code> والذي يكافئ <code>O(E+V)*LogV)</code> وتساوي <code>O(ELogV)</code>. (في الرسوم البيانية المتّصلة <code>V = O(E)</code>). | يمكن تخفيض التعقيد الزمني لهذه الخوارزمية إلى المقدار <code>O(ELogV)</code> باستخدام قائمة المجاورة لتمثيل الرسم البياني. تنفّذ العبارات البرمجية في حلقتي <code>while</code> التكراريتين بتعقيد زمني قدره <code>O(V+E)</code> (تشبه خوارزمية البحث بالعرض أولًا). وتتضمن الحلقة الداخلية العملية <code>decreaseKey()</code> والتي تستغرق <code>O(LogV)</code> من الوقت؛ لذا فإنّ التعقيد الزمني الكلي هو <code>O(E+V) * O(LogV)</code> والذي يكافئ <code>O(E+V)*LogV)</code> وتساوي <code>O(ELogV)</code>. (في الرسوم البيانية المتّصلة <code>V = O(E)</code>). | ||
== انظر أيضًا == | |||
* [[Algorithms/Kruskal MST|خوارزمية كروسكال لإيجاد الشجرة الممتدة الصغرى]]: تعثر خوارزمية كروسكال Kruskal على الشجرة الممتدة الصغرى في الرسم البياني المعطى، بترتيب الأضلاع تصاعديًا ثم اختيار الضلع الأصغر. | |||
== مصادر == | == مصادر == | ||
المراجعة الحالية بتاريخ 10:04، 20 أكتوبر 2019
تبدأ هذه الخوارزمية بشجرة ممتدة فارغة، وتعتمد في عملها مجموعتين من الرؤوس. تحتوي المجموعة الأولى على الرؤوس المضافة فعلًا إلى الشجرة الممتدة الصغرى، أما المجموعة الأخرى فتضمّ الرؤوس غير المضافة بعد. وفي كل خطوة، تنظر الخوارزمية في جميع الأضلاع التي تربط المجموعتين، وتختار الضلع ذا الوزن الأقل من بين الأضلاع. وبعد ذلك تحرّك نقطة النهاية الأخرى لهذا الضلع إلى المجموعة التي تحتوي على الشجرة الممتدة الصغرى.
تسمى مجموعة الأضلاع التي تربط بين مجموعتي رؤوس في الرسم البياني بالمقطع cut في نظرية المجموعات. وفي كل خطوة من خطوات خوارزمية برم Prim نجد مقطعًا (من مجموعتين، إحداهما تحتوي على الرؤوس المضافة فعلًا إلى الشجرة الممتدة الصغرى والأخرى تحتوي على بقية الرؤوس)، فنختار الضلع ذا الوزن الأقل من المقطع ونضيف هذا الرأس إلى مجموعة الشجرة الممتدة الصغرى.
طريقة عمل الخوارزمية
المبدأ العام لهذه الخوارزمية هو أنّ الشجرة الممتدة تعني لزوم ارتباط جميع الرؤوس بعضها ببعض، لذا فإنّ مجموعتي الرؤوس الفرعيتين المنفصلتين (اللتين ورد ذكرهما في أعلاه) يجب أن تكونا متصلتين لإنشاء شجرة ممتدة، ويجب أن تكونا متصلتين كتذلك مع الضلع ذي الوزن الأقل لكي تصبح الشجرة شجرة ممتدة صغرى.
يمكن تقسيم خوارزمية برم إلى الخطوات التالية:
- إنشاء مجموعة (ليكن اسمها
mstSet) تُضاف إليه الرؤوس التي أضيفت فعلًا إلى الشجرة الممتدة الصغرى. - تعيين قيمة مفتاحية لجميع الرؤوس في الرسم البياني المعطى، ثم تهيئة جميع القيم لتكون ما لا نهاية
INFINITE، وإسناد القيمة0إلى الرأس الأول وذلك ليكون أول رأس يجري اختياره. - تنفيذ الخطوات التالية ما دامت
mstSetلا تتضمن جميع الرؤوس:- اختيار رأس (ليكن
u) بشرط أن لا يكون موجودا فيmstSetويمتلك أقل قيمة مفتاحية. - إضافة الرأس
uإلى المجموعةmstSet. - تحديث القيم المفتاحية لجميع الرؤوس المجاورة للرأس
u. ولتحديث القيم المفتاحية تمر الخوارزمية على جميع الرؤوس المجاورة لهذا الرأس، ولكل رأس مجاور (ليكنv) إن كان وزن الضلعu-vأقل من القمية المفتاحية السابقة للرأسv، تحدّث القيمة المتفاحية لتكون وزن الضلعu-v.
- اختيار رأس (ليكن
الهدف من استخدام القيم المفتاحية هو اختيار الضلع ذي الوزن الأقل من المقطع المحدد. لا تستخدم القيم المفتاحية إلا مع الرؤوس التي لم تضف بعد إلى الشجرة الممتدة الصغرى إذا تشير القيمة المفتاحية لهذه الرؤوس إلى الأضلاع ذات الأوزان الأقل التي تربطها بمجموعة الرؤوس المضافة إلى الشجرة الممتدة الصغرى.
يوضّح المثال التالي خطوات عمل الخوارزمية:
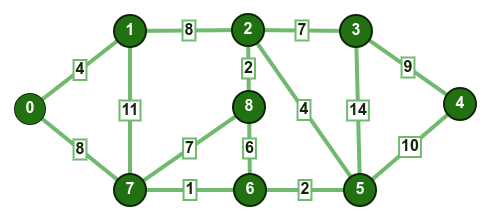
تكون المجموعة mstSet فارغة في البداية والمفاتيح المسندة إلى الرؤوس هي {0, INF, INF, INF, INF, INF, INF, INF} (تمثل INF اللانهاية). نختار الرأس الذي يمتلك أقل قيمة مفتاحية، -وهو في هذه الحالة الرأس 0- ونضيفه إلى مجموعة mstSet، فتصبح المجموعة {0}، وبعدها نحدث القيم المفتاحية للرؤوس المجاورة وهما الرأسان 1 و 7 إلى القيم 4 و 8. يعرض الرسم البياني التالي الرؤوس التي تم العمل عليها والقيم المفتاحية الخاصة بها، ويعرض الرسم البياني الرؤوس التي تمتلك قيمة محددة فقط، وتحمل الرؤوس المضافة إلى الشجرة الممتدة الصغرى اللون الأحمر.
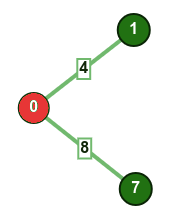
نختار الرأس الذي يمتلك القيمة المفتاحية الأقل بشرط أن لا يكون موجودًا في المجموعة mstSet. في هذه الحالة سنختار الرأس 1 ونضيفه إلى المجموعة mstSet لتصبح بالنتيجة {0, 1}. نحدث بعد ذلك القيمة المفتاحية للرؤوس المجاورة للرأس 1، وبذلك تحدّث القيمة المفتاحية للرأس 2 إلى القيمة 8.
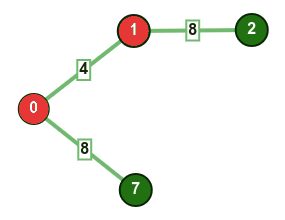
نختار الرأس الذي يمتلك القيمة المفتاحية الأقل بشرط أن لا يكون موجودًا في المجموعة mstSet. في هذه الحالة يمكن اختيار أحد الرأسين 7 أو 2، وسنفترض أن الاختيار قد وقع على الرأس 7، لذا ستصبح المجموعة mstSet الآن {0, 1, 7}. نحدّث بعد ذلك القيمة المفتاحية للرؤوس المجاورة للرأس 7، وبذلك تحدّث القيمة المفتاحية للرأسين 6 و 8 إلى القيمتين 1 و 7 على التوالي.
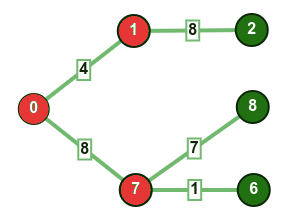
نختار الرأس الذي يمتلك القيمة المفتاحية الأقل بشرط أن لا يكون موجودًا في المجموعة mstSet. في هذه الحالة سنختار الرأس 6 ونضيفه إلى المجموعة mstSet لتصبح بالنتيجة {0, 1, 7, 6}. نحدث بعد ذلك القيمة المفتاحية للرؤوس المجاورة للرأس 6، وبذلك تحدّث القيمة المفتاحية للرأسين 5 و 8.
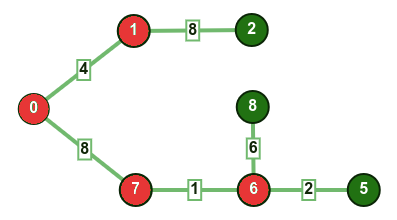
تكرّر الخطوات السابقة إلى حين دخول جميع الرؤوس في مجموعة mstSet؛ وفي النهاية سنحصل على الرسم البياني التالي:
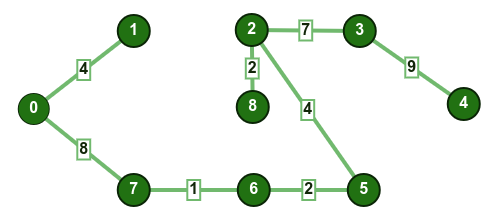
تنفيذ الخوارزمية
يمكن استخدام مصفوفة منطقية (لتكن mstSet[] لتمثيل مجموعة الرؤوس المضافة إلى الشجرة الممتدة الصغرى. فإن كانت قيمة mstSet[v] صحيحة، فإن الرأس v سيُضاف إلى الشجرة الممتدة الصغرى، وإلا فلا. تستخدم المصفوفة key[] لتخزين القيم المفتاحية لجميع الرؤوس، وتستخدم المصفوفة parent[] لتخزين مواقع العقد الأبوية في الشجرة الممتدة الصغرى، وهذه المصفوفة هي مصفوفة المخرجات أيضًا وتستخدم لعرض الشجرة الممتدة الصغرى التي تم بناؤها.
تعرض الأمثلة التالية طريقة تنفيذ الخوارزمية في عدد من لغات البرمجة:
- C++:
#include <bits/stdc++.h>
using namespace std;
// عدد الرؤوس في الرسم البياني
#define V 5
// دالة مساعدة مهمتها العثور على الرأس
// الذي يحمل القيمة المفتاحية الأقل من مجموعة الرؤوس
// غير المضافة بعد إلى الشجرة الممتدة الصغرى
int minKey(int key[], bool mstSet[])
{
// min تهيئة قيمة
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
// دالة مساعددة وظيفتها طباعة
// parent[] الشجرة الممتدة الصغرى المخزنة في المصفوفة
int printMST(int parent[], int graph[V][V])
{
cout<<"Edge \tWeight\n";
for (int i = 1; i < V; i++)
cout<<parent[i]<<" - "<<i<<" \t"<<graph[i][parent[i]]<<" \n";
}
// تبني هذه الدالة الشجرة الممتدة الصغرى وتطبع النتيجة
// تستخدم هذه الدالة الرسم البياني الممثل بواسطة مصفوفة المجاورة
void primMST(int graph[V][V])
{
// المصفوفة المسؤولة عن تخزين الشجرة الممتدة الصغرى التي يجري بناؤها
int parent[V];
// القيم المفتاحية المستخدم لالتقاط الضلع ذي الوزن الأقل في المقطع
int key[V];
// لتمثيل مجموعة الرؤوس غير المضافة بعد إلى الشجرة الممتدة الصغرى
bool mstSet[V];
// تهيئة جميع المفاتيح لتحمل القيمة ما لا نهاية
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
// نضيف الرأس الأول دائمًا إلى الشجرة الممتدة الصغرى
// نجعل قيمة المفتاح 0 لتختار الدالة هذا الرأس في البداية
key[0] = 0;
parent[0] = -1; // العقدة الأولى هي دائمًا جذر الشجرة الممتدة الصغرى
// ستمتلك الشجرة الممتدة الصغرى عدد الرؤوس المعطى
for (int count = 0; count < V - 1; count++)
{
// اختيار الرأس ذي القيمة المفتاحية الأقل من
// مجموعة الرؤوس التي لم تضف بعد إلى الشجرة الممتدة الصغرى
int u = minKey(key, mstSet);
// إضافة الرأس المنتخب إلى مجموعة الشجرة الممتدة الصغرى
mstSet[u] = true;
// تحديث القيمة المفتاحية والآباء للرؤوس المجاورة للرأس المنتخب
// تجري عملية التحديث فقط على الرؤوس غير المضافة بعد إلى الشجرة الممتدة الصغرى
for (int v = 0; v < V; v++)
// graph[u][v]
// هذه القيمة لا تساوي صفرًا للرؤوس المجاورة فقط
// mstSet[v]
// هذه القيمة تكون خاطئة للرؤوس غير المضافة بعد إلى الشجرة الممتدة الصغرى
// يجري تحديث المفتاح فقط إذا كانت
// graph[u][v] < key[v]
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
// طباعة الشجرة الممتدة التي قد تم بناؤها
printMST(parent, graph);
}
// اختبار الدوال السابقة
int main()
{
/* إنشاء الرسم البياني التالي
2 3
(0)--(1)--(2)
| / \ |
6| 8/ \5 |7
| / \ |
(3)-------(4)
9 */
int graph[V][V] = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
// طباعة الحل
primMST(graph);
return 0;
}
- بايثون
import sys # INT_MAX نستورد هذه الوحدة لاستخدام
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
# parent[] دالة مساعدة لطباعة الشجرة الممتدة الصغرى التي تم إنشاؤها والمخزنة في
def printMST(self, parent):
print "Edge \tWeight"
for i in range(1, self.V):
print parent[i], "-", i, "\t", self.graph[i][ parent[i] ]
# دالة مساعدة للعثور على الرأس الذي يمتلك أقل قيمة للمسافة
# من مجموعة الرؤوس غير المضافة بعد إلى شجرة المسار الأقصر
def minKey(self, key, mstSet):
# min تهيئة قيمة
min = sys.maxint
for v in range(self.V):
if key[v] < min and mstSet[v] == False:
min = key[v]
min_index = v
return min_index
# تبني هذه الدالة الشجرة الممتدة الصغرى للرسم البياني المعطى وتطبعها
# تستخدم هذه الدالة الرسوم البيانية الممثلة بواسطة مصفوفة المجاورة
def primMST(self):
# القيم المفتاحية المستخدمة لاختيار الضلع الذي يمتلك أقل وزن في المقطع
key = [sys.maxint] * self.V
parent = [None] * self.V # تستخدم هذه القائمة لتخزين الشجرة الممتدة الصغرى
# نجعل القمية المفتاحية للرأس الأول صفرًا وذلك لتختاره الدالة في البداية
key[0] = 0
mstSet = [False] * self.V
parent[0] = -1 # تكون العقدة الأولى جذر الشجرة الممتدة الصغرى دائمًا
for cout in range(self.V):
# اختيار الرأس ذي المسافة الأقصر من مجموعة
# الرؤوس التي لم تخضع للمعالجة بعد
# يكون الرأس الحالي هو المصدر في الدورة الأولى دائمًا
u = self.minKey(key, mstSet)
# إضافة الرأس ذي المسافة الأقصر إلى شجرة المسار الأقصر
mstSet[u] = True
# تحديث قيمة المسافة للرؤوس المجاورة
# للرأس المنتخب بشرط أن تكون المسافة الحالية
# أكبر من المسافة الجديدة وأن لا يكون
# الرأس موجودًا في شجرة المسار الأقصر
for v in range(self.V):
# graph[u][v]
# هذه القيمة لا تساوي صفرًا للرؤوس المجاورة فقط
# mstSet[v]
# هذه القيمة تكون خاطئة للرؤوس غير المضافة بعد إلى الشجرة الممتدة الصغرى
# يجري تحديث المفتاح فقط إذا كانت
# graph[u][v] < key[v]
if self.graph[u][v] > 0 and mstSet[v] == False and key[v] > self.graph[u][v]:
key[v] = self.graph[u][v]
parent[v] = u
self.printMST(parent)
g = Graph(5)
g.graph = [ [0, 2, 0, 6, 0],
[2, 0, 3, 8, 5],
[0, 3, 0, 0, 7],
[6, 8, 0, 0, 9],
[0, 5, 7, 9, 0]]
g.primMST();
- جافا
import java.util.*;
import java.lang.*;
import java.io.*;
class MST {
// عدد الرؤوس في الرسم البياني
private static final int V = 5;
// دالة مساعدة مهمتها العثور على الرأس
// الذي يحمل القيمة المفتاحية الأقل من مجموعة الرؤوس
// غير المضافة بعد إلى الشجرة الممتدة الصغرى
int minKey(int key[], Boolean mstSet[])
{
// min تهيئة قيمة
int min = Integer.MAX_VALUE, min_index = -1;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
return min_index;
}
// دالة مساعددة وظيفتها طباعة
// parent[] الشجرة الممتدة الصغرى المخزنة في المصفوفة
void printMST(int parent[], int graph[][])
{
System.out.println("Edge \tWeight");
for (int i = 1; i < V; i++)
System.out.println(parent[i] + " - " + i + "\t" + graph[i][parent[i]]);
}
// تبني هذه الدالة الشجرة الممتدة الصغرى وتطبع النتيجة
// تستخدم هذه الدالة الرسم البياني الممثل بواسطة مصفوفة المجاورة
void primMST(int graph[][])
{
// المصفوفة المسؤولة عن تخزين الشجرة الممتدة الصغرى التي يجري بناؤها
int parent[] = new int[V];
// القيم المفتاحية المستخدم لالتقاط الضلع ذي الوزن الأقل في المقطع
int key[] = new int[V];
// لتمثيل مجموعة الرؤوس غير المضافة بعد إلى الشجرة الممتدة الصغرى
Boolean mstSet[] = new Boolean[V];
// تهيئة جميع المفاتيح لتحمل القيمة ما لا نهاية
for (int i = 0; i < V; i++) {
key[i] = Integer.MAX_VALUE;
mstSet[i] = false;
}
// نضيف الرأس الأول دائمًا إلى الشجرة الممتدة الصغرى
// نجعل قيمة المفتاح 0 لتختار الدالة هذا الرأس في البداية
key[0] = 0;
parent[0] = -1; // العقدة الأولى هي دائمًا جذر الشجرة الممتدة الصغرى
// ستمتلك الشجرة الممتدة الصغرى عدد الرؤوس المعطى
for (int count = 0; count < V - 1; count++) {
// اختيار الرأس ذي القيمة المفتاحية الأقل من
// مجموعة الرؤوس التي لم تضف بعد إلى الشجرة الممتدة الصغرى
int u = minKey(key, mstSet);
// إضافة الرأس المنتخب إلى مجموعة الشجرة الممتدة الصغرى
mstSet[u] = true;
// تحديث القيمة المفتاحية والآباء للرؤوس المجاورة للرأس المنتخب
// تجري عملية التحديث فقط على الرؤوس غير المضافة بعد إلى الشجرة الممتدة الصغرى
for (int v = 0; v < V; v++)
// graph[u][v]
// هذه القيمة لا تساوي صفرًا للرؤوس المجاورة فقط
// mstSet[v]
// هذه القيمة تكون خاطئة للرؤوس غير المضافة بعد إلى الشجرة الممتدة الصغرى
// يجري تحديث المفتاح فقط إذا كانت
// graph[u][v] < key[v]
if (graph[u][v] != 0 && mstSet[v] == false && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
// طباعة الشجرة الممتدة التي قد تم بناؤها
printMST(parent, graph);
}
// اختبار الدوال السابقة
public static void main(String[] args)
{
/* إنشاء الرسم البياني التالي
2 3
(0)--(1)--(2)
| / \ |
6| 8/ \5 |7
| / \ |
(3)-------(4)
9 */
MST t = new MST();
int graph[][] = new int[][] { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
// طباعة الحل
t.primMST(graph);
}
}
تنفيذ الخوارزمية على الرسوم البيانية الممثلة بواسطة قائمة المجاورة
في حال استخدام قوائم المجاورة لتمثيل الرسم البياني، فإن بالإمكان المرور على جميع الرؤوس في الرسم البياني بتعقيد زمني قدره O(V+E) وذلك باستخدام خوارزمية البحث بالعرض أولًا Breadth first search. يتلخص عمل الخوارزمية بهذه الطريقة في المرور على جميع الرؤوس في الرسم البياني باستخدام خوارزمية البحث بالعرض أولًا واستخدام كومة صغرى Min Heap لتخزين الرؤوس غير المضافة بعد إلى الشجرة الممتدة الصغرى. تستخدم الكومة الصغرى كرتل أولوية priority queue للحصول على الضلع الذي يمتلك أقل وزن في المقطع. إن سبب استخدام الكومة الصغرى هو أنّ التعقيد الزمني لعمليات مثل استخراج العنصر الأصغر وإنقاص القيمة المفتاحية تبلغ فيها المقدار O(LogV).
ويمكن تقسيم عمل الخوارزمية إلى الخطوات التالية:
- إنشاء كومة صغرى حجمها
Vوتمثّل عدد الرؤوس في الرسم البياني المعطى. تحتوي كل عقدة في الكومة الصغرى على رقم الرأس والقيمة المفتاحية الخاصة به. - تهيئة الكومة الصغرى ليكون الرأس الأول في الرسم البياني جذرًا لها (القيمة المفتاحية المسنة إلى الرأس الأول هي `0). تُسند القيمة المفتاحية (ما لا نهاية) إلى بقية الرؤوس.
- إجراء الخطوات التالية بشرط أن لا تكون الكومة الصغرى فارغة:
- استخراج العقدة ذات القيمة الأصغر من الكومة الصغرى (لتكن
u). - لكل عقدة
vمجاورة للعقدةu، نتحقّق من أنّvموجودة في الكومة الصغرى (ليست مضافة بعد إلى الشجرة الممتدة الصغرى). إن كانتvموجود في الكومة الصغرى وكانت قيمتها المفتاحية أكبر من وزن الضلعu-v، فسنحدث القيمة المفتاحية للعقدةvلتكون مساوية لوزن الضلعu-v.
- استخراج العقدة ذات القيمة الأصغر من الكومة الصغرى (لتكن
يمكن توضيح الخطوات السابقة بالمثال التالي:

في البداية، تعطى القيمة المفتاحية 0 للرأس الأول والقيمة INF (ما لا نهاية) لبقية الرؤوس. يُستخرج الرأس 0 من الكومة الصغرى وتحدث القيمة المفتاحية للرؤوس المجاورة له (وهما الرأسان 1 و 7). تحتوي الكومة الصغرى على جميع الرؤوس باستثناء الرأس 0.
الرؤوس الملونة باللون الأحمر هي الرؤوس المضافة إلى الشجرة الممتدة الصغرى.

لما كانت القيمة المفتاحية للرأس 1 هي أصغر قيمة بين جميع العقد في الكومة الصغرى، تستخرج الخوارزمية هذه القيمة من الكومة الصغرى وتحدث القيمة المفتاحية للرؤوس المجاورة للرأس 1 (تحدث القيمة المفتاحية للرأس إذا لم يكن في الكومة الصغرى وكانت القيمة المفتاحية السابقة أكبر من وزن الضلع الذي يربط الرأس 1 بالرأس المجاور له). تحتوي الكومة الصغرى على جميع الرؤوس باستثناء الرأسين 0 و 1.

لما كانت القيمة المفتاحية للرأس 7 هي أصغر قيمة بين جميع العقد في الكومة الصغرى، تستخرج الخوارزمية هذه القيمة من الكومة الصغرى وتحدث القيمة المفتاحية للرؤوس المجاورة للرأس 7 (تحدث القيمة المفتاحية للرأس إذا لم يكن في الكومة الصغرى وكانت القيمة المفتاحية السابقة أكبر من وزن الضلع الذي يربط الرأس 7 بالرأس المجاور له). تحتوي الكومة الصغرى على جميع الرؤوس باستثناء الرؤوس 0 و 1 و 7.

لما كانت القيمة المفتاحية للرأس 1 هي أصغر قيمة بين جميع العقد في الكومة الصغرى، تستخرج الخوارزمية هذه القيمة من الكومة الصغرى وتحدث القيمة المفتاحية للرؤوس المجاورة للرأس 6 (تحدث القيمة المفتاحية للرأس إذا لم يكن في الكومة الصغرى وكانت القيمة المفتاحية السابقة أكبر من وزن الضلع الذي يربط الرأس 6 بالرأس المجاور له). تحتوي الكومة الصغرى على جميع الرؤوس باستثناء الرؤوس 0 و 1 و 7 و 6.

تكرّر الخطوات السابقة على جميع العقد في الكومة الصغرى إلى أن تصبح فارغة.

أمثلة
تعرض الأمثلة التالية طريقة تنفيذ خوارزمية برم على الرسوم البيانية الممثلة بواسطة قائمة المجاورة:
- C++:
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
// تمثيل عقدة في قائمة المجاورة
struct AdjListNode {
int dest;
int weight;
struct AdjListNode* next;
};
// تمثيل قائمة المجاورة
struct AdjList {
struct AdjListNode* head; // مؤشر إلى عقدة الرأس في القائمة
};
// تمثيل الرسم البياني. الرسم البياني عبارة عن مصفوفة من قوائم المجاورة.
// V حجم المصفوفة سيكون
// عدد الرؤوس في الرسم البياني
struct Graph {
int V;
struct AdjList* array;
};
// دالة مساعدة لإنشاء عقدة جديدة في قائمة المجاورة
struct AdjListNode* newAdjListNode(int dest, int weight)
{
struct AdjListNode* newNode = (struct AdjListNode*)malloc(sizeof(struct AdjListNode));
newNode->dest = dest;
newNode->weight = weight;
newNode->next = NULL;
return newNode;
}
// دالة مساعدة لإنشاء رسم بياني من الرؤوس المعطاة
struct Graph* createGraph(int V)
{
struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
graph->V = V;
// إنشاء مصفوفة من قوائم المجاورة.
// V حجم المصفوفة سيكون
graph->array = (struct AdjList*)malloc(V * sizeof(struct AdjList));
// NULL تهيئة كل قائمة مجاورة لتكون فارغة وذلك بجعل الرأس يحمل القيمة
for (int i = 0; i < V; ++i)
graph->array[i].head = NULL;
return graph;
}
// تضيف الدالة ضلعًا إلى الرسم البياني غير الموجّه
void addEdge(struct Graph* graph, int src, int dest, int weight)
{
// إضافة ضلع من الوجهة إلى الهدف. تضاف عقدة جديدة إلى قائمة المجاورة الخاصة بالمصدر.
// تضاف العقدة في البداية.
struct AdjListNode* newNode = newAdjListNode(dest, weight);
newNode->next = graph->array[src].head;
graph->array[src].head = newNode;
// لما كان الرسم البياني غير موجّه، نضيف الضلع من الهدف إلى الوجهة كذلك
newNode = newAdjListNode(src, weight);
newNode->next = graph->array[dest].head;
graph->array[dest].head = newNode;
}
// تمثيل عقدة في الكومة الصغرى
struct MinHeapNode {
int v;
int key;
};
// تمثيل كومة صغرى
struct MinHeap {
int size; // عدد عقد الكومة الموجودة فعلًا
int capacity; // سعة الكومة الصغرى
int* pos; // decreaseKey() مطلوب من قبل الدالة
struct MinHeapNode** array;
};
// دالة مساعدة لإنشاء عقدة جديدة في الكومة الصغرى
struct MinHeapNode* newMinHeapNode(int v, int key)
{
struct MinHeapNode* minHeapNode = (struct MinHeapNode*)malloc(sizeof(struct MinHeapNode));
minHeapNode->v = v;
minHeapNode->key = key;
return minHeapNode;
}
// دالة مساعدة لإنشاء كومة صغرى
struct MinHeap* createMinHeap(int capacity)
{
struct MinHeap* minHeap = (struct MinHeap*)malloc(sizeof(struct MinHeap));
minHeap->pos = (int*)malloc(capacity * sizeof(int));
minHeap->size = 0;
minHeap->capacity = capacity;
minHeap->array = (struct MinHeapNode**)malloc(capacity * sizeof(struct MinHeapNode*));
return minHeap;
}
// دالة مساعدة للتبديل بين عقدتين في الكومة الصغرى. نحتاج إلى هذه الدالة لبناء الكومة الصغرى
void swapMinHeapNode(struct MinHeapNode** a, struct MinHeapNode** b)
{
struct MinHeapNode* t = *a;
*a = *b;
*b = t;
}
// دالة قياسية لإنشاء الكومة عند الفهرس المعطى
// تحدث هذه الدالة كذلك موقع العقد عند التبديل بينها
// decreaseKey() الموقع مطلوب من قبل الدالة
void minHeapify(struct MinHeap* minHeap, int idx)
{
int smallest, left, right;
smallest = idx;
left = 2 * idx + 1;
right = 2 * idx + 2;
if (left < minHeap->size && minHeap->array[left]->key < minHeap->array[smallest]->key)
smallest = left;
if (right < minHeap->size && minHeap->array[right]->key < minHeap->array[smallest]->key)
smallest = right;
if (smallest != idx) {
// العقد التي يجب التبديل بينها في الكومة الصغرى
MinHeapNode* smallestNode = minHeap->array[smallest];
MinHeapNode* idxNode = minHeap->array[idx];
// تبديل المواقع
minHeap->pos[smallestNode->v] = idx;
minHeap->pos[idxNode->v] = smallest;
// تبديل العقد
swapMinHeapNode(&minHeap->array[smallest], &minHeap->array[idx]);
minHeapify(minHeap, smallest);
}
}
// دالة مساعدة للتحق من فراغ الكومة الصغرى
int isEmpty(struct MinHeap* minHeap)
{
return minHeap->size == 0;
}
// دالة قياسية لاستخراج العقدة الصغرى من الكومة
struct MinHeapNode* extractMin(struct MinHeap* minHeap)
{
if (isEmpty(minHeap))
return NULL;
// تخزين عقدة الجذر
struct MinHeapNode* root = minHeap->array[0];
// استبدال عقدة الجذر بالعقدة الأخيرة
struct MinHeapNode* lastNode = minHeap->array[minHeap->size - 1];
minHeap->array[0] = lastNode;
// تحديث موقع العقدة الأخيرة
minHeap->pos[root->v] = minHeap->size - 1;
minHeap->pos[lastNode->v] = 0;
// تقليص حجم الكومة وبناء الكومة من الجذر
--minHeap->size;
minHeapify(minHeap, 0);
return root;
}
// تقلّص هذه الدالة القيمة المفتاحية لرأس معين.
// تستخدم هذه الدالة مصفوفة المواقع الخاصة بالكومة الصغرى للحصول على موقع العقدة في الكومة الصغرى
void decreaseKey(struct MinHeap* minHeap, int v, int key)
{
// الحصول على موقع الرأس في مصفوفة الكومة
int i = minHeap->pos[v];
// الحصول على العقدة وتحديث القيمة المفتاحية لها
minHeap->array[i]->key = key;
// التنقل صعودًا ما دامت الشجرة الكاملة لم تحول إلى كومة
// O(Logn) تعمل هذه الحلقة التكرارية بتعقيد زمني قدره
while (i && minHeap->array[i]->key < minHeap->array[(i - 1) / 2]->key) {
// تبديل هذه العقدة بالعقدة الأم
minHeap->pos[minHeap->array[i]->v] = (i - 1) / 2;
minHeap->pos[minHeap->array[(i - 1) / 2]->v] = i;
swapMinHeapNode(&minHeap->array[i], &minHeap->array[(i - 1) / 2]);
// التحرك إلى موقع العقدة الأم
i = (i - 1) / 2;
}
}
// دالة مساعدة للتحقق من أنّ الرأس المعطى
// موجود في الكومة الصغرى أم لا
bool isInMinHeap(struct MinHeap* minHeap, int v)
{
if (minHeap->pos[v] < minHeap->size)
return true;
return false;
}
// دالة مساعدة مهمتها طباعة الشجرة الممتدة الصغرى التي تم بناؤها
void printArr(int arr[], int n)
{
for (int i = 1; i < n; ++i)
printf("%d - %d\n", arr[i], i);
}
// الدالة الرئيسية المسؤولة عن بناء الشجرة الممتدة الصغرى
// باستخدام خوارزمية برم
void PrimMST(struct Graph* graph)
{
int V = graph->V; // الحصول على عدد الرؤوس في الرسم البياني
int parent[V]; // مصفوفة تخزن فيها الشجرة الممتدة الصغرى
int key[V]; // القيم المفتاحية التي تستخدم لاختيار الضلع ذي الوزن الأقل في المقطع
// E تمثل الكومة الصغرى المجموعة
struct MinHeap* minHeap = createMinHeap(V);
// تهيئة الكومة الصغرى مع جميع الرؤوس.
//تحمل جميع الرؤوس (باستثناء الرأس الصفري) قيمة اللانهاية كقيمة ابتدائية
for (int v = 1; v < V; ++v) {
parent[v] = -1;
key[v] = INT_MAX;
minHeap->array[v] = newMinHeapNode(v, key[v]);
minHeap->pos[v] = v;
}
// جعل القمية المفتاحية للرأس الصفري مساوية للصفر
// وذلك ليُستخرج هذا الرأس أولًا
key[0] = 0;
minHeap->array[0] = newMinHeapNode(0, key[0]);
minHeap->pos[0] = 0;
// في البداية يكون حجم الكومة الصغرى مساويًا لعدد الأضلع
minHeap->size = V;
// تحتوي الكومة الصغرى في هذه الحلقة التكرارية على جميع العقد
// غير المضافة بعد إلى الشجرة الممتدة الصغرى
while (!isEmpty(minHeap)) {
// استخراج الرأس الذي يمتلك القيمة المفتاحية الأصغر
struct MinHeapNode* minHeapNode = extractMin(minHeap);
int u = minHeapNode->v; // تخزين القيمة المفتاحية المستخرجة
// التنقل عبر جميع الرؤوس المجاورة للرأس الحالي (المستخرج)
// وتحديث القيمة المفتاحية لها
struct AdjListNode* pCrawl = graph->array[u].head;
while (pCrawl != NULL) {
int v = pCrawl->dest;
// إن لم يكن الرأس المجاور مضافًا إلى الشجرة الممتدة الصغرى
// u-v وكان وزن الضلع الذي يربط بين الرأسين
// v أصغر من القيمة المفتاحية للضلع المجاور
// نحدث القيمة المفتاحية للرأس المجاور والعقدة الأم له
if (isInMinHeap(minHeap, v) && pCrawl->weight < key[v]) {
key[v] = pCrawl->weight;
parent[v] = u;
decreaseKey(minHeap, v, key[v]);
}
pCrawl = pCrawl->next;
}
}
// طباعة الأضلاع الموجودة في الشجرة الممتدة الصغرى
printArr(parent, V);
}
// اختبار الدوال السابقة
int main()
{
// إنشاء الرسم البياني أعلاه
int V = 9;
struct Graph* graph = createGraph(V);
addEdge(graph, 0, 1, 4);
addEdge(graph, 0, 7, 8);
addEdge(graph, 1, 2, 8);
addEdge(graph, 1, 7, 11);
addEdge(graph, 2, 3, 7);
addEdge(graph, 2, 8, 2);
addEdge(graph, 2, 5, 4);
addEdge(graph, 3, 4, 9);
addEdge(graph, 3, 5, 14);
addEdge(graph, 4, 5, 10);
addEdge(graph, 5, 6, 2);
addEdge(graph, 6, 7, 1);
addEdge(graph, 6, 8, 6);
addEdge(graph, 7, 8, 7);
PrimMST(graph);
return 0;
}
- بايثون
from collections import defaultdict
import sys
class Heap():
def __init__(self):
self.array = []
self.size = 0
self.pos = []
def newMinHeapNode(self, v, dist):
minHeapNode = [v, dist]
return minHeapNode
# دالة مساعدة للتبديل بين عقدتين في الكومة الصغرى
# هذه الدالة ضرورية لبناء الكومة
def swapMinHeapNode(self, a, b):
t = self.array[a]
self.array[a] = self.array[b]
self.array[b] = t
# دالة قياسية لبناء الكومة في الموقع المعطى
# تحدث هذه الدالة كذلك مواقع العقد عند التبديل بينها
# decreaseKey() الموقع مطلوب من قبل الدالة
def minHeapify(self, idx):
smallest = idx
left = 2 * idx + 1
right = 2 * idx + 2
if left < self.size and self.array[left][1] < \
self.array[smallest][1]:
smallest = left
if right < self.size and self.array[right][1] < \
self.array[smallest][1]:
smallest = right
# العقد المراد التبديل بينها في الكومة الصغرى
# إن كان الموقع هو الأصغر
if smallest != idx:
# تبديل المواقع
self.pos[ self.array[smallest][0] ] = idx
self.pos[ self.array[idx][0] ] = smallest
# التبديل بين العقد
self.swapMinHeapNode(smallest, idx)
self.minHeapify(smallest)
# دالة قياسية لاستخراج العقدة الأصغر من الكومة
def extractMin(self):
# الخروج من الدالة إن كانت الكومة فارغة
if self.isEmpty() == True:
return
# تخزين عقدة الجذر
root = self.array[0]
# التبديل بين عقدة الجذر والعقدة الأخيرة
lastNode = self.array[self.size - 1]
self.array[0] = lastNode
# تحديث موقع العقدة الأخيرة
self.pos[lastNode[0]] = 0
self.pos[root[0]] = self.size - 1
# تقليص حجم الكومة وبناؤها من الجذر
self.size -= 1
self.minHeapify(0)
return root
def isEmpty(self):
return True if self.size == 0 else False
def decreaseKey(self, v, dist):
# الحصول على موقع العقدة المجاورة في مصفوفة الكومة
i = self.pos[v]
# الحصول على العقدة وتحديث قيمة الوجهة المسافة الخاصة بها
self.array[i][1] = dist
# التنقل صعودًا ما لم تتكون كومة من الشجرة الكاملة
# O(Logn) التعقيد الزمني لهذه الحلقة هو
while i > 0 and self.array[i][1] < \
self.array[(i - 1) / 2][1]:
# التبديل بين هذه العقدة والعقدة الأم
self.pos[ self.array[i][0] ] = (i-1)/2
self.pos[ self.array[(i-1)/2][0] ] = i
self.swapMinHeapNode(i, (i - 1)/2 )
# الانتقال إلى موقع العقدة الأم
i = (i - 1) / 2;
# دالة مساعدة مهمتها التحقق من وجود
# الراأس المعطى في الكومة
def isInMinHeap(self, v):
if self.pos[v] < self.size:
return True
return False
def printArr(parent, n):
for i in range(1, n):
print "% d - % d" % (parent[i], i)
class Graph():
def __init__(self, V):
self.V = V
self.graph = defaultdict(list)
# تضيف الدالة ضلعًا غلى الرسم البياني غير الموجّه
def addEdge(self, src, dest, weight):
# يضاف الضلع من المصدر إلى الوجهة
# تضاف عقدة جديدة في قائمة المجاورة الخاصة بالمصدر
# تضاف العقدة في البداية
# يمثل العنصر الأول في العقدة المسافة
# ويمثل العنصر الثاني الوزن
newNode = [dest, weight]
self.graph[src].insert(0, newNode)
# لما كان الرسم البياني غير موجّه
# سنضيف ضلعًا من الوجهة إلى المصدر أيضًا
newNode = [src, weight]
self.graph[dest].insert(0, newNode)
# الدالة الرئيسية التي تطبع نتيجة تنفيذ
# خوارزمية برم للشجرة الممتدة الصغرى
# O(ELogV) التعقيد الزمني لهذه الدالة هو
def PrimMST(self):
# الحصول على عدد الرؤوس في الرسم البياني
V = self.V
# القيم المفتاحية المستخدمة لاختيار الأضلاع ذات الأوزان الأقل في المقطع
key = []
# تستخدم هذه القائمة لتخزين الشجرة الممتدة الصغرى التي قد تم بناؤها
parent = []
# تمثل الكومة الصغرى مجموعة الأضلاع
minHeap = Heap()
# تهيئة الكومة الصغرى مع جميع الرؤوس
# تكون القيمة المفتاحية لجميع الرؤوس هي (ما لا نهاية)
# باستثناء الرأس الأول
for v in range(V):
parent.append(-1)
key.append(sys.maxint)
minHeap.array.append( minHeap.newMinHeapNode(v, key[v]) )
minHeap.pos.append(v)
# جعل القيمة المفتاحية للرأس الأول مساوية للصفر
# وذلك لاستخراجه من الكومة أولًا
minHeap.pos[0] = 0
key[0] = 0
minHeap.decreaseKey(0, key[0])
# تهيئة حجم الكومة الصغرى ليكون مساويًا لعدد الرؤوس
minHeap.size = V;
# تحتوي الكومة الصغرى في هذه الحلقة على جميع العقد
# غير المضافة بعد إلى الشجرة الممتدة الصغرى
while minHeap.isEmpty() == False:
# استخراج الرأس الذي يمتلك أقل قيمة للمسافة
newHeapNode = minHeap.extractMin()
u = newHeapNode[0]
# التنقل عبر جميع الرؤوس المجاورة للرأس الحالي
# (الرأس المستخرج من الكومة الصغرى)
# وتحديث قيم المسافة لها
for pCrawl in self.graph[u]:
v = pCrawl[0]
# إن لم تنتهِ الخوارزمية من حساب المسافة الأقصر للرأس المجاور
# وإن كانت المسافة بين الراس أقصر من المسافة المحسوبة سابقًا
if minHeap.isInMinHeap(v) and pCrawl[1] < key[v]:
key[v] = pCrawl[1]
parent[v] = u
# نحدث قيمة المسافة في الكومة الصغرى أيضًا
minHeap.decreaseKey(v, key[v])
printArr(parent, V)
# اختبار الدوال السابقة
graph = Graph(9)
graph.addEdge(0, 1, 4)
graph.addEdge(0, 7, 8)
graph.addEdge(1, 2, 8)
graph.addEdge(1, 7, 11)
graph.addEdge(2, 3, 7)
graph.addEdge(2, 8, 2)
graph.addEdge(2, 5, 4)
graph.addEdge(3, 4, 9)
graph.addEdge(3, 5, 14)
graph.addEdge(4, 5, 10)
graph.addEdge(5, 6, 2)
graph.addEdge(6, 7, 1)
graph.addEdge(6, 8, 6)
graph.addEdge(7, 8, 7)
graph.PrimMST()
- جافا:
ملاحظة:
تستخدم هذه الشيفرة كائن TreeSet عوضًا عن رتل الأولوية PriorityQueue وذلك لأنّ دالة الحذف في رتل الأولوية تعمل بتعقيد زمني قدره O(n) في لغة جافا.
import java.util.LinkedList;
import java.util.TreeSet;
import java.util.Comparator;
public class prims {
class node1 {
// تخزين رأس الوجهة في قائمة المجاورة
int dest;
// تخزين وزن الرأس في قائمة المجاورة
int weight;
node1(int a, int b)
{
dest = a;
weight = b;
}
}
static class Graph {
// عدد الرؤوس في الرسم البياني
int V;
// قائمة العقد المجاورة للرأس المعطى
LinkedList<node1>[] adj;
Graph(int e)
{
V = e;
adj = new LinkedList[V];
for (int o = 0; o < V; o++)
adj[o] = new LinkedList<>();
}
}
// يستخدم هذا الصنف لتمثيل العقدة في رتل الأولوية
// يخزن هذا الصنف العقدة والقيمة المفتاحية المرتطبة بها
class node {
int vertex;
int key;
}
// صنف مقارنة ينشأ من رتل الأولوية
// node0.key > node1.key يعيد القيمة 1 إن تحقق الشرط
// node0.key < node1.key يعيد القيمة 0 إن تحقق الشرط
// ويعيد القيمة -1 فيما عدا ذلك
class comparator implements Comparator<node> {
@Override
public int compare(node node0, node node1)
{
return node0.key - node1.key;
}
}
// يضيف التابع ضلعًا بين رأسين
void addEdge(Graph graph, int src, int dest, int weight)
{
node1 node0 = new node1(dest, weight);
node1 node = new node1(src, weight);
graph.adj[src].addLast(node0);
graph.adj[dest].addLast(node);
}
// يستخدم هذا التابع للعثور على الشجرة الممتدة الصغرى
void prims_mst(Graph graph)
{
// التحقق من أنّ الرأس موجود في رتل الأولوية أم لا
Boolean[] mstset = new Boolean[graph.V];
node[] e = new node[graph.V];
// هنا تخزن العقد الأم لرأس معين
int[] parent = new int[graph.V];
for (int o = 0; o < graph.V; o++)
e[o] = new node();
for (int o = 0; o < graph.V; o++) {
// إسناد قيمة خاطئة
mstset[o] = false;
// تهيئة القيمة المفتاحية لتأخذ قيمة (ما لا نهاية)
e[o].key = Integer.MAX_VALUE;
e[o].vertex = o;
parent[o] = -1;
}
// mstset تضمين الرأس المصدر في
mstset[0] = true;
// تهيئة القيمة المفتاحية لتكون صفرًا
// وذلك لكي يكون أول رأس يُستخرج من رتل الأولوية
e[0].key = 0;
// راجع الملاحظة في بداية الشيفرة
TreeSet<node> queue = new TreeSet<node>(new comparator());
for (int o = 0; o < graph.V; o++)
queue.add(e[o]);
// تعمل هذه الحلقة ما دام الرتل غير فارغ
while (!queue.isEmpty()) {
// استخراج العقدة التي تمتلك أقل قيمة مفتاحية
node node0 = queue.pollFirst();
// mstset إضافة تلك العقدة إلى
mstset[node0.vertex] = true;
// تمرّ هذه الحلقة على جميع الرؤوس المجاورة للرأس المستخرج
for (node1 iterator : graph.adj[node0.vertex]) {
// إن كان الرأس المستخرج موجودًا في الرتل
if (mstset[iterator.dest] == false) {
// إن كانت القيمة المفتاحية للرأس المجاور
// أكبر من القيمة المستخرجة
// نحدث القيمة المفتاحية للرأس المجاور
// ولإجراء التحديث نحذف الرأس ونضيف الرأس المحدث
if (e[iterator.dest].key > iterator.weight) {
queue.remove(e[iterator.dest]);
e[iterator.dest].key = iterator.weight;
queue.add(e[iterator.dest]);
parent[iterator.dest] = node0.vertex;
}
}
}
}
// تطبع هذه الحلقة أزواج الرؤوس في الشجرة الممتدة الصغرى
for (int o = 1; o < graph.V; o++)
System.out.println(parent[o] + " "
+ "-"
+ " " + o);
}
public static void main(String[] args)
{
int V = 9;
Graph graph = new Graph(V);
prims e = new prims();
e.addEdge(graph, 0, 1, 4);
e.addEdge(graph, 0, 7, 8);
e.addEdge(graph, 1, 2, 8);
e.addEdge(graph, 1, 7, 11);
e.addEdge(graph, 2, 3, 7);
e.addEdge(graph, 2, 8, 2);
e.addEdge(graph, 2, 5, 4);
e.addEdge(graph, 3, 4, 9);
e.addEdge(graph, 3, 5, 14);
e.addEdge(graph, 4, 5, 10);
e.addEdge(graph, 5, 6, 2);
e.addEdge(graph, 6, 7, 1);
e.addEdge(graph, 6, 8, 6);
e.addEdge(graph, 7, 8, 7);
e.prims_mst(graph);
}
}
تعطي الشيفرات السابقة المخرجات التالية:
0 - 1
5 - 2
2 - 3
3 - 4
6 - 5
7 - 6
0 - 7
2 - 8
التعقيد الزمني
التعقيد الزمني لخوارزمية برم هو O(V^2).
يمكن تخفيض التعقيد الزمني لهذه الخوارزمية إلى المقدار O(ELogV) باستخدام قائمة المجاورة لتمثيل الرسم البياني. تنفّذ العبارات البرمجية في حلقتي while التكراريتين بتعقيد زمني قدره O(V+E) (تشبه خوارزمية البحث بالعرض أولًا). وتتضمن الحلقة الداخلية العملية decreaseKey() والتي تستغرق O(LogV) من الوقت؛ لذا فإنّ التعقيد الزمني الكلي هو O(E+V) * O(LogV) والذي يكافئ O(E+V)*LogV) وتساوي O(ELogV). (في الرسوم البيانية المتّصلة V = O(E)).
انظر أيضًا
- خوارزمية كروسكال لإيجاد الشجرة الممتدة الصغرى: تعثر خوارزمية كروسكال Kruskal على الشجرة الممتدة الصغرى في الرسم البياني المعطى، بترتيب الأضلاع تصاعديًا ثم اختيار الضلع الأصغر.
مصادر
- صفحة Prim’s Minimum Spanning Tree في توثيق الخوارزميات في موقع GeeksforGeeks.
- صفحة Prim’s MST for Adjacency List Representation في توثيق الخوارزميات في موقع GeeksforGeeks.