Algorithms/linked lists

لقوائم المترابطة هLinked Lists ي بنى معطيات خطية لا تخزّن فيها العناصر في مواقع متجاورة في الذاكرة.،تورتبط العناصر بعضها ببعض في القوائم المترابطة بواسطة المؤشرات وكما هو موضّح في الصورة التالية:

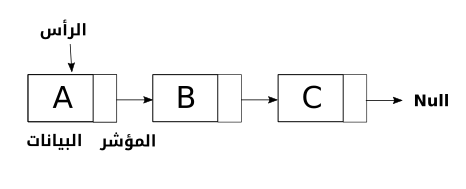
ويمكن القول أنّ القوائم المترابطة تتكوّن من عقد، وتحتوي كل عقدة منها على حقل بيانات وإشارة (رابطة) إلى العقدة التالية في القائمة.

لماذا تستخدم القوائم المترابطة

يمكن استخدام المصفوفات لتخزين البيانات الخطية التي تكون من النوع ذاته، ولكن يعيب المصفوفات ما يلي:

1. حجم المصفوفات ثابت، وهذا يعني أنّه يجب علينا معرفة الحد الأقصى للعناصر التي ستدخل في المصفوفة مسبقًا، إلى جانب أنّ المساحة المحجوزة في الذاكرة تكون مساوية للحد الأقصى للمصفوفة بصرف النظر عن عدد العناصر الموجودة فيها فعلًا.
2. تستهلك عملية إضافة عنصر جديد إلى المصفوفة الكثير من الذاكرة؛ وذلك لأنّ إضافة عنصر جديد تعني إيجاد مكان له في المصفوفة، وهذا الأمر يعني بدوره إزاحة العناصر الموجودة في المصفوفة عن مواقعها.

لنفرض -على سبيل المثال- أنّ لدينا قائمة من المعرّفات المرتبة في مصفوفة: id[] = [1000, 1010, 1050, 2000, 2040]‎.

لو أردنا إضافة معرّف جديد يحمل القيمة 1005 دون الإخلال بترتيب العناصر، فيتحتّم علينا حينئذٍ تحريك جميع العناصر التي تلي المعرّف 1000.

عملية الحذف مكلفة أيضًا، إلا إذا استخدمنا بعض التقنيات الخاصة. فعلى سبيل المثال لنتمكّن من حذف المعرّف 1010 في المصفوفة السابقة يجب علينا تحريك جميع العناصر التي تلي المعرّف 1010.

القوائم المترابطة والمصفوفات

تختلف القوائم المترابطة عن المصفوفات بالنقاط التالية:

1. المصفوفة هي بنية معطيات تحتوي على مجموعة من عناصر ذات نوع متشابه، في حين أنّ القوائم المترابطة تُعدّ من بنى المعطيات غير البدائية والتي تحتوي على مجموعة من العناصر المترابطة وغير المرتبة والتي تدعى بالعقد.
2. تنتمي العناصر في المصفوفات إلى فهارس، بمعنى أنّه لغرض الوصول إلى العنصر الرابع في المصفوفة يجب كتابة اسم المتغير مع فهرسه أو موقعه ضمن أقواس مربعة.
3. أما في القوائم المترابطة فيجب البدء من الرأس ثم المرور على العناصر واحدًا تلو الآخر إلى حين الوصول إلى العنصر الرابع.
4. يمكن الوصول إلى عنصر ما في المصفوفة بسرعة، أما القوائم المترابطة فإنّ الوصول إلى العناصر فيها يأخذ وقتًا خطيًّا أكثر؛ ولهذا تكون القوائم المترابطة أبطأ قليلًا مقارنة بالمصفوفات.
5. تستهلك عمليات مثل الإضافة والحذف الكثير من الوقت في المصفوفات، ولكنّها تكون سريعة في القوائم المترابطة.
6. حجم المصفوفات ثابت، وذلك على عكس القوائم المترابطة التي تكون ذات حجم متغير وتمتاز بالمرونة والقابلية على تكبير أو تصغير حجمها حسب الحاجة.
7. تُسند المعلومات إلى الذاكرة عن استخدام المصفوفات في وقت التصريف compile time، أما عند استخدام القوائم المترابطة فإنّ الذاكرة تُحجز في وقت التشغيل أو التنفيذ runtime.
8. تخزن العناصر في المصفوفة بالترتيب، وتخزّن في القوائم المترابطة بصورة عشوائية.
9. تتطلب المصفوفات مقدارًا أقل من الذاكرة وذلك نظرًا لتخزين البيانات الفعلية ضمن الفهرس، أما القوائم المترابطة فتحتاج بالمقابل إلى مقدار أكبر من الذاكرة وذلك لحاجتها إلى تخزين عناصر إضافية للإشارة إلى العقد السابقة واللاحقة.
10. لا يمكن استخدام الذاكرة بكفاءة مع المصفوفات، وذلك على عكس القوائم المترابطة.

عيوب القوائم المترابطة

1. لا يمكن الوصول إلى عناصر القوائم المترابطة بطريقة عشوائية، بل يجب الوصول إلى العناصر بالترتيب بدءًا من العقدة الأولى؛ ولذا لا يمكن إجراء عملية البحث الثنائي binary search بكفاءة إن استخدمنا الطريقة الافتراضية للتعامل مع القوائم المترابطة.
2. يحتاج كل عنصر إلى مساحة إضافية في الذاكرة لارتباط كل عنصر بمؤشر.
3. ليست ملائمة للذاكرة الخبيئة. لمّا كانت عناصر المصفوفة في مواقع متجاورة، فإن الإشارات إلى العناصر تكون في موقع واحد locality of reference، وهو أمر تفتقده القوائم المترابطة.

تمثيل القوائم المترابطة

تمثّل القائمة المترابطة بواسطة مؤشر pointer إلى العقدة الأولى في القائمة المترابطة. تدعى العقدة الأولى بالرأس head، وإن كانت القائمة المترابطة فارغة، فإنّ قيمة الرأس تكون NULL.

تتكوّن كل عقدة في القائمة من جزئين:

1. البيانات.
2. مؤشر Pointer (أو إشارة Reference) إلى العقدة التالية.

يمكن تمثيل العقدة في لغة C باستخدام البنى structures. يبين المثال التالي عقدة قائمة مترابطة مع بيانات عددية.

struct Node 
{ 
  int data; 
  struct Node *next; 
};

• Java, C#‎

أما في لغتي Java و C#‎ فيمكن تمثيل القوائم المترابطة بواسطة صنف والعقد بواسطة صنف آخر منفصل، ويحتوي صنف القائمة المترابطة على إشارة إلى صنف العقدة.

// C#
class LinkedList 
{ 
	Node head; 

	class Node 
	{ 
		int data; 
		Node next; 
		
        // دالة بانية لإنشاء عقدة جديدة
		Node (int d) {data = d;} 
	} 
}

//Java
class LinkedList 
{ 
    Node head;
  
    // العقدة
    class Node 
    { 
        int data; 
        Node next; 
           
        // دالة بانية لإنشاء عقدة جديدة
        // أما القيمة العقدة اللاحقة فتهيئ تلقائيًا
        // null إلى القيمة
        Node(int d) {data = d;} 
    } 
}

• بايثون:

# Node class 
class Node: 
   
    # دالة لتهيئة كائن العقدة
    def __init__(self, data): 
        self.data = data  # إسناد البيانات
        self.next = None  # تهيئة العقدة التالية لتكون فارغة 
   
# صنف القائمة المترابطة
class LinkedList: 
     
    # دالة لتهيئة كائن القائمة المترابطة  
    def __init__(self):  
        self.head = None

إضافة العقد إلى القوائم المترابطة

تستخدم جميع الأمثلة المعروضة في هذه الصفحة طريقة التمثيل التالية للقوائم المترابطة:

struct Node 
{ 
  int data; 
  struct Node *next; 
};

يمكن إضافة العقد إلى القائمة المترابطة في مواضع ثلاث هي:

1. في بداية القائمة المترابطة.

1. بعد عقدة معينة.

1. في نهاية القائمة المترابطة.

إضافة عقدة إلى بداية القائمة المترابطة

تضاف العقدة الجديدة دائمًا قبل الرأس الخاص بالقائمة المترابطة، وتصبح العقدة الجديدة رأس تلك القائمة. فعلى سبيل المثال إن كان لدينا القائمة المترابطة التالية: 10->15->20->25 وأضفنا الرقم 5 إلى بداية القائمة، فإنّها ستصبح بالصورة التالية: 5->10->15->20->25.

لو أسمينا الدالة التي ستضيف العنصر الجديد إلى بداية القائمة المترابطة بالاسم push()‎ فيجب على هذه الدالة أن تستقبل مؤشرًا خاصًّا بمؤشر الرأس؛ وذلك لوجوب إشارة هذا المؤشر إلى العقدة الجديدة.

إنّ مقدار تعقيد الوقت الخاص بالدالة push()‎ هو O(1)‎ وذلك لأنّها تؤدي مقدارًا ثابتًا من العمل.

إضافة عقدة بعد عقدة موجودة

يكون لدينا في هذه الحالة مؤشر إلى عقدة معينة، ونرغب في إضافة عقدة جديدة بعدها.

إن مقدار تعقيد الوقت الخاص بالدالة insertAfter()‎ هو O(q)‎ لأنّها تؤدي مقدارًا ثابتًا من العمل.

إضافة عقدة إلى نهاية القائمة المترابطة

تضاف العقدة الجديدة دائمًا بعد العقدة الأخيرة في القائمة المترابطة. فعلى سبيل المثال إن كانت لدينا القائمة المترابطة التالية: 5->10->15->20->25 وأردنا إضافة العنصر 30 إلى نهاية القائمة، فإنّ القائمة المترابطة تصبح بالصورة التالية: 5->10->15->20->25->30.

ولما كان الرأس يمثّل القائمة المترابطة عادةً، فيجب علينا أن نمر على عناصر القائمة وصولًا إلى نهايتها، ثم تغيير العقدة التالية للعقدة الأخيرة لتصبح العقدة الجديدة.

يكون مقدار تعقيد الوقت لهذه العملية هو O(n)‎ وتمثل n عد العقد الموجودة في القائمة المترابطة، ولما كان المرور على عناصر القائمة جزءًا من عمل الدالة، فإنّ الدالة تؤدي O(n)‎ من العمل.

يمكن تحسين عمل هذه الدالة لتعمل بمقدار تعقيد O(1)‎ وذلك بالإبقاء على مؤشر إضافي في نهاية القائمة المترابطة.

أمثلة

تعرض الأمثلة التالية طرق الإضافة الثلاثة وفي عدد من لغات البرمجة:

• C++‎

#include <bits/stdc++.h> 
using namespace std; 

// عقدة قائمة مترابطة
class Node 
{ 
	public: 
	int data; 
	Node *next; 
}; 

/* إدراج عقدة جديدة في مقدّمة القائمة
باستخدام الإشارة (مؤشر إلى المؤشر) إلى رأس القائمة
والعدد الصحيح المعطى */
void push(Node** head_ref, int new_data) 
{ 
	/* 1. حجز موقع العقدة في الذاكرة */
	Node* new_node = new Node(); 

	/* 2. إضافة البيانات */
	new_node->data = new_data; 

	/* 3. جعل رأس القائمة هو العقدة التالية للعقدة الجديدة */
	new_node->next = (*head_ref); 

	/* 4. تحريك رأس القائمة ليشير إلى العقدة الجديدة */
	(*head_ref) = new_node; 
} 

/* إدراج عقدة بعد العقدة السابقة المعطاة */
void insertAfter(Node* prev_node, int new_data) 
{ 
	/*1. Null التحقق من أنّ العقدة السابقة المعطاة تحمل القيمة */
	if (prev_node == NULL) 
	{ 
		cout<<"the given previous node cannot be NULL"; 
		return; 
	} 

	/* 2. حجز موقع العقدة الجديدة في الذاكرة */
	Node* new_node = new Node(); 

	/* 3. إضافة البيانات */
	new_node->data = new_data; 

	/* 4. جعل العقدة اللاحقة للعقدة الجديدة هي العقدة اللاحقة للعقدة السابقة */
	new_node->next = prev_node->next; 

	/* 5. تحريك العقدة التالية للعقدة السابقة لتصبح العقدة الجديدة */
	prev_node->next = new_node; 
} 

/* إلحاق عقدة جديدة في نهاية القائمة باستخدام
الإشارة (مؤشر إلى مؤشر) إلى رأس القائمة والعدد الصحيح المعطى */

void append(Node** head_ref, int new_data) 
{ 
	/* 1. حجز موقع العقدة الجديدة في الذاكرة */
	Node* new_node = new Node(); 

	Node *last = *head_ref; /* يستخدم في الخطوة 5*/

	/* 2. إدراج البيانات */
	new_node->data = new_data; 

	/* 3. ستكون العقدة الجديدة هي العقدة الأخير في القائمة
	لذا سنجعل العقدة اللاحقة لها هي
	NULL*/
	new_node->next = NULL; 

	/* 4. إن كانت القائمة فارغةً
	ستكون العقدة الجديدة في رأس القائمة*/
	if (*head_ref == NULL) 
	{ 
		*head_ref = new_node; 
		return; 
	} 

	/* 5. وإن لم تكن القائمة فارغة ننقل العقدة الجديدة إلى نهاية القائمة */
	while (last->next != NULL) 
		last = last->next; 

	/* 6. نغير العقدة اللاحقة للعقدة الأخيرة. */
	last->next = new_node; 
	return; 
} 

// تطبع هذه الدالة محتويات القائمة المترابطة
// بدءًا من رأس القائمة
void printList(Node *node) 
{ 
	while (node != NULL) 
	{ 
		cout<<" "<<node->data; 
		node = node->next; 
	} 
} 

// اختبار الدوال السابقة
int main() 
{ 
	/* البدء بقائمة فارغة */
	Node* head = NULL; 
	
	// إدراج العنصر 6
	// لتصبح القائمة بالشكل التالي
    // 6->NULL 
	append(&head, 6); 
	
	// إدراج العنصر 7 في بداية القائمة 
	// فتصبح القائمة بالشكل التالي
    // 7->6->NULL 
	push(&head, 7); 
	
	// إدراج العنصر 1 في بداية القائمة
    // فتصبح القائمة بالشكل التالي
    // 1->7->6->NULL 
	push(&head, 1); 
	
	// إدراج العنصر 4 في نهاية القائمة
    // فتصبح القائمة بالشكل التالي
	append(&head, 4); 
	
	// إدراج العنصر 8 بعد العنصر 7
    // لتصبح القائمة بالشكل التالي
	insertAfter(head->next, 8); 
	
	cout<<"Created Linked list is: "; 
	printList(head); 
	
	return 0; 
}

مصادر

• https://www.geeksforgeeks.org/data-structures/linked-list/

• https://www.geeksforgeeks.org/linked-list-set-1-introduction/

• https://www.geeksforgeeks.org/linked-list-set-2-inserting-a-node/