الفرق بين المراجعتين لصفحة: «Algorithms/binary search trees»
لا ملخص تعديل |
|||
| سطر 312: | سطر 312: | ||
تظهر ثلاثة احتمالات عند حذف عقدة من شجرة البحث الثنائية: | تظهر ثلاثة احتمالات عند حذف عقدة من شجرة البحث الثنائية: | ||
'''1- العقدة المراد حذفها هي عقدة ورقية leaf''': تُحذف هذه العقدة من الشجرة مباشرة. | '''1- العقدة المراد حذفها هي عقدة ورقية leaf''': تُحذف هذه العقدة من الشجرة مباشرة.<syntaxhighlight lang="text"> | ||
50 50 | |||
< | |||
/ \ delete(20) / \ | / \ delete(20) / \ | ||
30 70 ---------> 30 70 | 30 70 ---------> 30 70 | ||
/ \ / \ \ / \ | / \ / \ \ / \ | ||
20 40 60 80 40 60 80</ | 20 40 60 80 40 60 80 | ||
'''2- تمتلك العقدة المراد حذفها عقدة ابن واحدة فقط:''' تُنسخ العقدة الابن لتحل محل العقدة الأب وتحذف عقدة الابن. | </syntaxhighlight>'''2- تمتلك العقدة المراد حذفها عقدة ابن واحدة فقط:''' تُنسخ العقدة الابن لتحل محل العقدة الأب وتحذف عقدة الابن.<syntaxhighlight lang="text"> | ||
50 50 | |||
< | |||
/ \ delete(30) / \ | / \ delete(30) / \ | ||
30 70 ---------> 40 70 | 30 70 ---------> 40 70 | ||
\ / \ / \ | \ / \ / \ | ||
40 60 80 60 80</ | 40 60 80 60 80 | ||
</syntaxhighlight> | |||
< | '''3- تمتلك العقدة المراد حذفها عقدتي ابن اثنتين:''' نبحث عن العقدة اللاحقة الوسطية inorder successor لهذه العقدة، ثم ننسخ قيمة العقدة اللاحقة الوسطية ونحذفها. ويجدر التنبيه إلى أنّ بالإمكان استخدام العقدة السابقة الوسطية كذلك.<syntaxhighlight lang="text"> | ||
50 60 | |||
/ \ delete(50) / \ | / \ delete(50) / \ | ||
40 70 ---------> 40 70 | 40 70 ---------> 40 70 | ||
/ \ \ | / \ \ | ||
60 80 80</ | 60 80 80 | ||
</syntaxhighlight> | |||
يجب الانتباه إلى أنّ العقدة اللاحقة الوسطية مطلوبة فقط عندما يكون الفرع الأيمن للعقدة فارغًا، وفي المثال أعلاه يمكن الحصول على العقدة اللاحقة الوسطية عن طريق البحث عن أصغر قيمة في الفرع الأيمن للعقدة. | يجب الانتباه إلى أنّ العقدة اللاحقة الوسطية مطلوبة فقط عندما يكون الفرع الأيمن للعقدة فارغًا، وفي المثال أعلاه يمكن الحصول على العقدة اللاحقة الوسطية عن طريق البحث عن أصغر قيمة في الفرع الأيمن للعقدة. | ||
| سطر 338: | سطر 339: | ||
تعرض الأمثلة التالية طريقة حذف عقدة من شجرة البحث الثنائية في عدد من لغات البرمجة: | تعرض الأمثلة التالية طريقة حذف عقدة من شجرة البحث الثنائية في عدد من لغات البرمجة: | ||
* C++: | |||
< | <syntaxhighlight lang="c++"> | ||
#include<stdio.h> | |||
#include<stdlib.h> | #include<stdlib.h> | ||
| سطر 482: | سطر 484: | ||
return 0; | return 0; | ||
} | } | ||
</ | |||
</syntaxhighlight> | |||
* بايثون: | * بايثون: | ||
| سطر 772: | سطر 775: | ||
} | } | ||
</source> | </source> | ||
تعطي الشيفرات السابقة المخرجات التالية: | تعطي الشيفرات السابقة المخرجات التالية:<syntaxhighlight lang="text"> | ||
Inorder traversal of the given tree | |||
< | |||
20 30 40 50 60 70 80 | 20 30 40 50 60 70 80 | ||
Delete 20 | Delete 20 | ||
| سطر 784: | سطر 786: | ||
Delete 50 | Delete 50 | ||
Inorder traversal of the modified tree | Inorder traversal of the modified tree | ||
40 60 70 80</ | 40 60 70 80 | ||
تعرض الصور التالية أمثلة لتوضيح عملية الحذف: | </syntaxhighlight>تعرض الصور التالية أمثلة لتوضيح عملية الحذف: | ||
=== التعقيد الزمني === | === التعقيد الزمني === | ||
| سطر 797: | سطر 795: | ||
=== تحسين الشيفرة السابقة === | === تحسين الشيفرة السابقة === | ||
تستدعى الدالة <code>delete()</code> في الشيفرة السابقة تعادويًا على العقدة اللاحقة، ولكن يمكن تجنب الاستدعاءات التعاودية وذلك بتعقّب العقدة الأب للعقدة اللاحقة بحيث يمكننا حذف العقدة اللاحقة ببساطة عن طريق إعطاء القيمة <code>Null</code> للعقدة الابن التابع للعقدة الأب، إذ نحن نعلم مسبقًا أنّ العقدة اللاحقة ستكون دائمًا عقدة ورقية. | تستدعى الدالة <code>delete()</code> في الشيفرة السابقة تعادويًا على العقدة اللاحقة، ولكن يمكن تجنب الاستدعاءات التعاودية وذلك بتعقّب العقدة الأب للعقدة اللاحقة بحيث يمكننا حذف العقدة اللاحقة ببساطة عن طريق إعطاء القيمة <code>Null</code> للعقدة الابن التابع للعقدة الأب، إذ نحن نعلم مسبقًا أنّ العقدة اللاحقة ستكون دائمًا عقدة ورقية.<syntaxhighlight lang="c++"> | ||
#include <bits/stdc++.h> | |||
< | |||
using namespace std; | using namespace std; | ||
| سطر 941: | سطر 938: | ||
return 0; | return 0; | ||
} </ | } | ||
</syntaxhighlight> | |||
== مصادر == | == مصادر == | ||
* صفحة [https://www.geeksforgeeks.org/binary-search-tree-data-structure/ Binary search Trees] في توثيق بنى المعطيات في موقع GeeksforGeeks. | * صفحة [https://www.geeksforgeeks.org/binary-search-tree-data-structure/ Binary search Trees] في توثيق بنى المعطيات في موقع GeeksforGeeks. | ||
* صفحة [https://www.geeksforgeeks.org/binary-search-tree-set-2-delete/ Binary Search Tree | Set 2 (Delete)] في توثيق بنى المعطيات في موقع GeeksforGeeks. | * صفحة [https://www.geeksforgeeks.org/binary-search-tree-set-2-delete/ Binary Search Tree | Set 2 (Delete)] في توثيق بنى المعطيات في موقع GeeksforGeeks. | ||
[[تصنيف: الخوارزميات]] | [[تصنيف: الخوارزميات]] | ||
[[تصنيف: بنى المعطيات]] | [[تصنيف: بنى المعطيات]] | ||
مراجعة 13:26، 17 يونيو 2019
شجرة البحث الثنائي Binary Search Tree هي شجرة ثنائية تحتوي على عقد وتمتلك الخصائص التالية:
- يحتوي الفرع الأيسر من العقدة على عقد تمتلك مفاتيح ذات قيمة أقل من قيمة مفتاح هذه العقدة.
- يحتوي الفرع الأيمن من العقدة على عقد تمتلك مفاتيح ذات قيمة أكبر من قيمة مفتاح هذه العقدة.
- يجب أن يكون الفرع الأيمن والأيسر شجرتي بحث ثنائيتين أيضًا، ولا يمكن أن تكون هناك عقد متشابهة.
تفرض هذه الخصائص ترتيبًا خاصًّا للعناصر في شجرة البيانات الثنائية يعتمد على قيمة المفتاح، ونتيجة لذلك تزداد سرعة تنفيذ عمليات البحث والعثور على القيمة الدنيا أو العظمى؛ ولولا وجود هذا الترتيب لكان لزامًا علينا مقارنة جميع المفاتيح مع المفتاح المعطى للحصول على النتيجة المطلوبة.
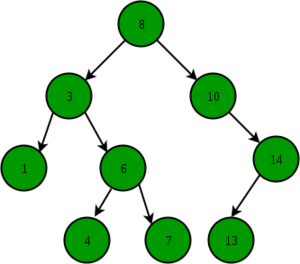
البحث عن مفتاح
تبدأ عملية البحث عن مفتاح معين في شجرة البحث الثنائية بمقارنة هذا المفتاح مع الجذر، فإن كان المفتاح المطلوب موجودًا في الجذر أعدناه، أمّا إذا كان المفتاح أكبر من الجذر أعدنا البحث في الفرع الأيمن من عقدة الجذر، وإن لم نعثر على المفتاح المطلوب أعدنا عملية البحث في الفرع الأيسر من العقدة.
أمثلة
تعرض الأمثلة التالية كيفية إجراء عملية البحث في شجرة البحث الثنائية وفي عدد من لغات البرمجة:
- C++:
struct node* search(struct node* root, int key)
{
// الحالة الأساسية: أن يكون الجذر فارغًا أو يكون المفتاح موجودًا في الجذر
if (root == NULL || root->key == key)
return root;
// المفتاح أكبر من مفتاح الجذر
if (root->key < key)
return search(root->right, key);
// المفتاح أصغر من مفتاح الجذر
return search(root->left, key);
}
- بايثون:
def search(root,key):
# الحالة الأساسية: أن يكون الجذر فارغًا أو يكون المفتاح موجودًا في الجذر
if root is None or root.val == key:
return root
# أن يكون المفتاح أكبر من مفتاح الجذر
if root.val < key:
return search(root.right,key)
# أن يكون المفتاح أصغر من مفتاح الجذر
return search(root.left,key)
- جافا:
public Node search(Node root, int key)
{
// الحالة الأساسية: أن يكون المفتاح فارغًا أو أن يكون المفتاح موجودًا في الجذر
if (root==null || root.key==key)
return root;
// أن يكون المفتاح أكبر من مفتاح الجذر
if (root.key > key)
return search(root.left, key);
// أن يكون المفتاح أصغر من مفتاح الجذر
return search(root.right, key);
}
- البحث عن العقدة 6 في الشجرة التالية:
- ابدأ البحث من الجذر.
- مقارنة العنصر المطلوب مع الجذر، فإن كان أقل منه أعدنا عملية البحث من العقدة الفرعية اليسرى، وإن كان أكبر من منه أعدنا عملية البحث من العقدة الفرعية اليمنى.
- إن عُثر على العنصر المطلوب في أي مكان نعيد قيمة صحيحة، وإلا أعدنا قيمة خاطئة.
إدراج مفتاح في شجرة البحث الثنائية
يُدرج العنصر الجديد دائمًا في عقد الأوراق، إذ نبدأ البحث عن مفتاح معين ابتداءً من الجذر وانتهاءً بعقدة الورقة، فإن عثرنا على عقدة ورقة ندرج العقدة الجديد كعقدة ابن لها.
100 100
/ \ Insert 40 / \
20 500 ---------> 20 500
/ \ / \
10 30 10 30
\
40
أمثلة
تعرض الأمثلة التالية طريقة إدراج عنصر في شجرة البحث الثنائية وفي عدد من لغات البرمجة:
- C++:
#include<stdio.h>
#include<stdlib.h>
struct node
{
int key;
struct node *left, *right;
};
// دالة مساعدة لإنشاء عقدة جديدة في شجرة البحث الثنائية
struct node *newNode(int item)
{
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// دالة مساعدة لإجراء عملية التنقل الوسطي في شجرة البحث الثنائية
void inorder(struct node *root)
{
if (root != NULL)
{
inorder(root->left);
printf("%d \n", root->key);
inorder(root->right);
}
}
/* دالة مساعدة لإدراج عقدة جديدة مع المفتاح المعطى في شجرة البحث الثنائية */
struct node* insert(struct node* node, int key)
{
/* إن كانت الشجرة فارغة، تعيد الدالة عقدة جديدة */
if (node == NULL) return newNode(key);
/* وإلا فإنّ الدالة تستدعي نفسها على الفرع الأيسر */
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
/* تعيد الدالة مؤشر العقدة */
return node;
}
// اختبار الدوال السابقة
int main()
{
/* للنشئ شجرة البحث الثنائي التالية
50
/ \
30 70
/ \ / \
20 40 60 80 */
struct node *root = NULL;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
// طباعة نتيجة عملية التنقل الوسطي
inorder(root);
return 0;
}
- بايثون:
# صنف مساعد يستخدم لتمثيل عقدة مفردة في شجرة البحث الثنائية
class Node:
def __init__(self,key):
self.left = None
self.right = None
self.val = key
# دالة مساعدة لإدراج عقدة جديدة مع المفتاح المعطى
def insert(root,node):
if root is None:
root = node
else:
if root.val < node.val:
if root.right is None:
root.right = node
else:
insert(root.right, node)
else:
if root.left is None:
root.left = node
else:
insert(root.left, node)
# دالة مساعدة لإجراء عملية التنقل الوسطي
def inorder(root):
if root:
inorder(root.left)
print(root.val)
inorder(root.right)
# اختبار الدوال السابقة
# لننشئ شجرة البحث الثنائية التالية
# 50
# / \
# 30 70
# / \ / \
# 20 40 60 80
r = Node(50)
insert(r,Node(30))
insert(r,Node(20))
insert(r,Node(40))
insert(r,Node(70))
insert(r,Node(60))
insert(r,Node(80))
# طباعة نتيجة التنقل الوسطي
inorder(r)
- جافا:
class BinarySearchTree {
// صنف يحتوي على العقدتين اليمنى واليسرى للعقدة الحالية وقيمة المفتاح
class Node {
int key;
Node left, right;
public Node(int item) {
key = item;
left = right = null;
}
}
// جذر شجرة البحث الثنائية
Node root;
// الدالة البانية
BinarySearchTree() {
root = null;
}
// insertRec يستدعي هذا التابع الدالة
void insert(int key) {
root = insertRec(root, key);
}
/* دالة تعاودية لإدراج مفتاح جديد في شجرة البحث الثنائية */
Node insertRec(Node root, int key) {
/* إن كانت الشجرة فارغة تعيد الدالة عقدة جديدة */
if (root == null) {
root = new Node(key);
return root;
}
/* وإلا تعيد الدالة استدعاء نفسها على فروع الشجرة */
if (key < root.key)
root.left = insertRec(root.left, key);
else if (key > root.key)
root.right = insertRec(root.right, key);
/* تعيد الدالة مؤشر العقدة */
return root;
}
// inorderRec يستدعي هذا التابع الدالة
void inorder() {
inorderRec(root);
}
// دالة مساعدة لإجراء عملية التنقل الوسطي في شجرة البحث الثنائية
void inorderRec(Node root) {
if (root != null) {
inorderRec(root.left);
System.out.println(root.key);
inorderRec(root.right);
}
}
// اختبار الدوال السابقة
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
/* لننشئ شجرة البحث الثنائية التالية
50
/ \
30 70
/ \ / \
20 40 60 80 */
tree.insert(50);
tree.insert(30);
tree.insert(20);
tree.insert(40);
tree.insert(70);
tree.insert(60);
tree.insert(80);
// طباعة نتيجة عملية التنقل الوسطي
tree.inorder();
}
}
تعطي الشيفرات السابقة المخرجات التالية:
20
30
40
50
60
70
80
مثال لإدراج العقدة 2 في الشجرة التالية:
- نبدأ من الجذر.
- نقارن العنصر المطلوب مع الجذر، فإن كان أصغر منه أعدنا عملية البحث في العقدة اليسرى، وإن كان أكبر منه أعدنا عملية البحث في العقدة اليمنى.
- بعد الوصول إلى نهاية الشجرة نُدرج العقدة في جهة اليسار (إن كانت أصغر من العقدة الحالية) وإلا أدرجناها في الجهة اليمنى.
التعقيد الزمني
إن أسوأ احتمال للتعقيد الزمني لعمليتي البحث والإدراج هو O(h) وتمثّل h ارتفاع شجرة البحث الثنائية. سنضطر في أسوأ الاحتمالات إلى التنقل عبر عناصر الشجرة من الجذر إلى آخر عقدة ورقية. في بعض الأحيان يمكن لارتفاع شجرة البيانات المائلة skewed أن يصبح n وعندها يصبح التعقيد الزمني لعمليتي الإدراج والبحث هو O(n).
حذف عقدة من شجرة البحث الثنائية
تظهر ثلاثة احتمالات عند حذف عقدة من شجرة البحث الثنائية:
1- العقدة المراد حذفها هي عقدة ورقية leaf: تُحذف هذه العقدة من الشجرة مباشرة.
50 50
/ \ delete(20) / \
30 70 ---------> 30 70
/ \ / \ \ / \
20 40 60 80 40 60 80
2- تمتلك العقدة المراد حذفها عقدة ابن واحدة فقط: تُنسخ العقدة الابن لتحل محل العقدة الأب وتحذف عقدة الابن.
50 50
/ \ delete(30) / \
30 70 ---------> 40 70
\ / \ / \
40 60 80 60 80
3- تمتلك العقدة المراد حذفها عقدتي ابن اثنتين: نبحث عن العقدة اللاحقة الوسطية inorder successor لهذه العقدة، ثم ننسخ قيمة العقدة اللاحقة الوسطية ونحذفها. ويجدر التنبيه إلى أنّ بالإمكان استخدام العقدة السابقة الوسطية كذلك.
50 60
/ \ delete(50) / \
40 70 ---------> 40 70
/ \ \
60 80 80
يجب الانتباه إلى أنّ العقدة اللاحقة الوسطية مطلوبة فقط عندما يكون الفرع الأيمن للعقدة فارغًا، وفي المثال أعلاه يمكن الحصول على العقدة اللاحقة الوسطية عن طريق البحث عن أصغر قيمة في الفرع الأيمن للعقدة.
أمثلة
تعرض الأمثلة التالية طريقة حذف عقدة من شجرة البحث الثنائية في عدد من لغات البرمجة:
- C++:
#include<stdio.h>
#include<stdlib.h>
struct node
{
int key;
struct node *left, *right;
};
// دالة مساعدة لإنشاء عقدة جديدة في شجرة البحث الثنائية
struct node *newNode(int item)
{
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// دالة مساعدة لإجراء عملية التنقل الوسطي في شجرة البحث الثنائية
void inorder(struct node *root)
{
if (root != NULL)
{
inorder(root->left);
printf("%d \n", root->key);
inorder(root->right);
}
}
/* دالة مساعدة لإدراج عقدة جديدة مع المفتاح المعطى في شجرة البحث الثنائية */
struct node* insert(struct node* node, int key)
{
/* إن كانت الشجرة فارغة، تعيد الدالة عقدة جديدة */
if (node == NULL) return newNode(key);
/* وإلا فإنّ الدالة تستدعي نفسها على الفرع الأيسر */
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
/* تعيد الدالة مؤشر العقدة */
return node;
}
/* لدينا شجرة بحث ثنائية غير فارغة، وسنعيد العقدة التي تمتلك أصغر قيمة للمفتاح في تلك الشجرة. لاحظ أنّه لا حاجة إلى البحث في الشجرة بأكملها */
struct node * minValueNode(struct node* node)
{
struct node* current = node;
/* استخدام الحلقة التكرارية لإيجاد أبعد ورقة إلى جهة اليسار */
while (current && current->left != NULL)
current = current->left;
return current;
}
/* لدينا شجرة بحث ثنائية ومفتاح، وستحذف هذه الدالة المفتاح وتعيد الجذر الجديد */
struct node* deleteNode(struct node* root, int key)
{
// الحالة الأساسية
if (root == NULL) return root;
// إن كان المفتاح المراد حذفه أصغر من مفتاح الجذر
// فإنه سيكون في الفرع الأيسر
if (key < root->key)
root->left = deleteNode(root->left, key);
// إن كان المفتاح المراد حذفه أصغر من مفتاح الجذر
// فإنه سيكون في الفرع الأيسر
else if (key > root->key)
root->right = deleteNode(root->right, key);
// إن كان المفتاح مماثلًا لمفتاح الجذر فهذه هي العقدة
// التي يجب حذفها
else
{
// عقدة لا تمتلك أبناء أو تمتلك عقدة ابن واحدة فقط
if (root->left == NULL)
{
struct node *temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL)
{
struct node *temp = root->left;
free(root);
return temp;
}
// عقدة تمتلك عقدتي أبناء، لذا سنحصل على العقدة اللاحقة الوسطية
// أصغر عقدة في الفرع الأيمن
struct node* temp = minValueNode(root->right);
// نسخ محتويات العقدة اللاحقة الوسطية إلى هذه العقدة
root->key = temp->key;
// حذف العقدة اللاحقة الوسطية
root->right = deleteNode(root->right, temp->key);
}
return root;
}
// اختبار الدوال السابقة
int main()
{
/* لننشئ شجرة البحث التالية
50
/ \
30 70
/ \ / \
20 40 60 80 */
struct node *root = NULL;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
printf("Inorder traversal of the given tree \n");
inorder(root);
printf("\nDelete 20\n");
root = deleteNode(root, 20);
printf("Inorder traversal of the modified tree \n");
inorder(root);
printf("\nDelete 30\n");
root = deleteNode(root, 30);
printf("Inorder traversal of the modified tree \n");
inorder(root);
printf("\nDelete 50\n");
root = deleteNode(root, 50);
printf("Inorder traversal of the modified tree \n");
inorder(root);
return 0;
}
- بايثون:
# عقدة في شجرة ثنائية
class Node:
# دالة بانية لإنشاء عقدة جديدة
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# دالة مساعدة لإجراء عملية التنقل الوسطي في شجرة البحث الثنائية
def inorder(root):
if root is not None:
inorder(root.left)
print root.key,
inorder(root.right)
# دالة مساعدة لإدراج عقدة جديدة مع المفتاح المعطى في شجرة البحث الثنائية
def insert( node, key):
# تعيد الدالة عقدة جديدة إن كانت الشجرة فارغة
if node is None:
return Node(key)
# وإلا فإن الدالة ستستدعي نفسها نزولًا في الشجرة
if key < node.key:
node.left = insert(node.left, key)
else:
node.right = insert(node.right, key)
# تعيد الدالة مؤشرة العقدة
return node
# لدينا شجرة بحث ثنائية غير فارغة، وسنعيد العقدة التي تمتلك أصغر
# قيمة للمفتاح في تلك الشجرة. لاحظ أنّه لا حاجة إلى البحث في الشجرة
# بأكملها
def minValueNode( node):
current = node
# استخدام الحلقة التكرارية لإيجاد أبعد ورقة إلى جهة اليسار
while(current.left is not None):
current = current.left
return current
# لدينا شجرة بحث ثنائية ومفتاح،
# وستحذف هذه الدالة المفتاح وتعيد الجذر الجديد
def deleteNode(root, key):
# الحالة الأساسية
if root is None:
return root
# إن كان المفتاح المراد حذفه أصغر من مفتح الجذر
# فإن هذا يعني أنّ المفتاح يقع في الفرع الأيسر
if key < root.key:
root.left = deleteNode(root.left, key)
# إن كان المفتاح المراد حذفه أكبر من مفتاح الجذر
# فإن هذا يعني أنّ المفتاح يقع في الفرع الأيمن
elif(key > root.key):
root.right = deleteNode(root.right, key)
# إن كان المفتاح ممامثلًأ لمفتاح الجذر، فهذا يعني أنّ هذه العقدة
# هي العقدة التي يجب حذفها
else:
# عقدة تمتلك ابنًا واحدًا أو لا تمتلك أبناء
if root.left is None :
temp = root.right
root = None
return temp
elif root.right is None :
temp = root.left
root = None
return temp
# عقدة تمتلك عقدتي أبناء. نحصل على العقدة اللاحقة الوسطية
# أصغر عقدة في الفرع الأيمن
temp = minValueNode(root.right)
# نسخ محتويات العقدة اللاحقة الوسطية إلى هذه العقدة
root.key = temp.key
# حذف العقدة اللاحقة الوسطية
root.right = deleteNode(root.right , temp.key)
return root
# اختبار الدوال السابقة
""" لننشئ شجرة البحث الثنائية التالية
50
/ \
30 70
/ \ / \
20 40 60 80 """
root = None
root = insert(root, 50)
root = insert(root, 30)
root = insert(root, 20)
root = insert(root, 40)
root = insert(root, 70)
root = insert(root, 60)
root = insert(root, 80)
print "Inorder traversal of the given tree"
inorder(root)
print "\nDelete 20"
root = deleteNode(root, 20)
print "Inorder traversal of the modified tree"
inorder(root)
print "\nDelete 30"
root = deleteNode(root, 30)
print "Inorder traversal of the modified tree"
inorder(root)
print "\nDelete 50"
root = deleteNode(root, 50)
print "Inorder traversal of the modified tree"
inorder(root)
- جافا:
class BinarySearchTree
{
/* صنف يتضمّن عقدتي الابن الأيسر والأيمن للعقدة الحالية إضافة إلى قيمة المفتاح */
class Node
{
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
// جذر شجرة البحث الثنائية
Node root;
// دالة بانية
BinarySearchTree()
{
root = null;
}
// deletRect تستخدم هذه الدالة لاستدعاء
void deleteKey(int key)
{
root = deleteRec(root, key);
}
// دالة تعاودية لإدراج مفتاح جديد في شجرة البحث الثنائية
Node deleteRec(Node root, int key)
{
// الحالة الأساسية: إن كانت الشجرة فارغة
if (root == null) return root;
// إن لم تكن الشجرة فارغة، تستدعي الدالة نفسها نزولًا في الشجرة
if (key < root.key)
root.left = deleteRec(root.left, key);
else if (key > root.key)
root.right = deleteRec(root.right, key);
// إن كان المفتاح مطابقًا لمفتاح الجذر، فهذه هي العقدة التي يجب حذفها
else
{
// عقدة تمتلك عقدة ابن واحدة أو لا تمتلك عقد أبناء
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// عقدة تمتلك عقدتي أبناء، نجلب العقدة اللاحقة الوسطية
// أصغر قيمة في الفرع الأيمن
root.key = minValue(root.right);
// حذف العقدة اللاحقة الوسطية
root.right = deleteRec(root.right, root.key);
}
return root;
}
int minValue(Node root)
{
int minv = root.key;
while (root.left != null)
{
minv = root.left.key;
root = root.left;
}
return minv;
}
// insertRec يستدعي هذا التابع الدالة
void insert(int key)
{
root = insertRec(root, key);
}
// دالة تعاودية لإدراج مفتاح جديد في شجرة البحث الثنائية
Node insertRec(Node root, int key)
{
// إن كانت الشجرة فارغة، تعيد الدالة عقدة جديدة
if (root == null)
{
root = new Node(key);
return root;
}
// إن لم تكن الشجرة فارغة، تستدعي الدالة نفسها نزولًا في الشجرة
if (key < root.key)
root.left = insertRec(root.left, key);
else if (key > root.key)
root.right = insertRec(root.right, key);
// تعيد الدالة مؤشر العقدة
return root;
}
// InorderRec يستخدم هذا التابع لاستدعاء
void inorder()
{
inorderRec(root);
}
// دالة مساعدة لإجراء عملية التنقل الوسطية في شجرة البحث الثنائية
void inorderRec(Node root)
{
if (root != null)
{
inorderRec(root.left);
System.out.print(root.key + " ");
inorderRec(root.right);
}
}
// اختبار الدوال السابقة
public static void main(String[] args)
{
BinarySearchTree tree = new BinarySearchTree();
/* لننشئ شجرة البحث الثنائية التالية:
50
/ \
30 70
/ \ / \
20 40 60 80 */
tree.insert(50);
tree.insert(30);
tree.insert(20);
tree.insert(40);
tree.insert(70);
tree.insert(60);
tree.insert(80);
System.out.println("Inorder traversal of the given tree");
tree.inorder();
System.out.println("\nDelete 20");
tree.deleteKey(20);
System.out.println("Inorder traversal of the modified tree");
tree.inorder();
System.out.println("\nDelete 30");
tree.deleteKey(30);
System.out.println("Inorder traversal of the modified tree");
tree.inorder();
System.out.println("\nDelete 50");
tree.deleteKey(50);
System.out.println("Inorder traversal of the modified tree");
tree.inorder();
}
}
تعطي الشيفرات السابقة المخرجات التالية:
Inorder traversal of the given tree
20 30 40 50 60 70 80
Delete 20
Inorder traversal of the modified tree
30 40 50 60 70 80
Delete 30
Inorder traversal of the modified tree
40 50 60 70 80
Delete 50
Inorder traversal of the modified tree
40 60 70 80
تعرض الصور التالية أمثلة لتوضيح عملية الحذف:
التعقيد الزمني
إن أسوأ احتمال للتعقيد الزمني لعمليتي البحث والإدراج هو O(h) وتمثّل h ارتفاع شجرة البحث الثنائية. سنضطر في أسوأ الاحتمالات إلى التنقل عبر عناصر الشجرة من الجذر إلى آخر عقدة ورقية. في بعض الأحيان يمكن لارتفاع شجرة البيانات المائلة skewed أن يصبح n وعندها يصبح التعقيد الزمني لعمليتي الإدراج والبحث هو O(n).
تحسين الشيفرة السابقة
تستدعى الدالة delete() في الشيفرة السابقة تعادويًا على العقدة اللاحقة، ولكن يمكن تجنب الاستدعاءات التعاودية وذلك بتعقّب العقدة الأب للعقدة اللاحقة بحيث يمكننا حذف العقدة اللاحقة ببساطة عن طريق إعطاء القيمة Null للعقدة الابن التابع للعقدة الأب، إذ نحن نعلم مسبقًا أنّ العقدة اللاحقة ستكون دائمًا عقدة ورقية.
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
struct Node *left, *right;
};
// دالة مساعدة لإنشاء عقدة في شجرة البحث الثنائية
Node* newNode(int item)
{
Node* temp = new Node;
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// دالة مساعددة لإجراء عملية التنقل الوسطي في عناصر شجرة البحث الثنائية
void inorder(Node* root)
{
if (root != NULL) {
inorder(root->left);
printf("%d ", root->key);
inorder(root->right);
}
}
// دالة مساعدة لإدراج عقدة جديدة مع المفتاح المعطى في شجرة البحث الثنائية
Node* insert(Node* node, int key)
{
// إن كانت الشجرة فارغة، تعيد الدالة عقدة جديدة
if (node == NULL)
return newNode(key);
// إن لم تكن الشجرة فارغة، تستدعي الدالة نفسها نزولاً في الشجرة
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
// تعيد الدالة مؤشر العقدة
return node;
}
/* لدينا شجرة بحث ثنائية ومفتاح، وستحذف هذه الدالة المفتاح وتعيد الجذر الجديد */
Node* deleteNode(Node* root, int k)
{
// الحالة الأساسية
if (root == NULL)
return root;
// استدعاءات تعاودية للعقد الأبوية التابعة
// للعقدة المراد حذفها
if (root->key > k) {
root->left = deleteNode(root->left, k);
return root;
}
else if (root->key < k) {
root->right = deleteNode(root->right, k);
return root;
}
// نصل إلى هنا حيث يكون الجذر هو العقدة
// المراد حذفها
// إن كان أحد الأبناء فارغًا
if (root->left == NULL) {
Node* temp = root->right;
delete root;
return temp;
}
else if (root->right == NULL) {
Node* temp = root->left;
delete root;
return temp;
}
// إن كان كلا الابنين موجودين
else {
Node* succParent = root->right;
// العثور على العقدة اللاحقة
Node *succ = root->right;
while (succ->left != NULL) {
succParent = succ;
succ = succ->left;
}
// نحذف العقدة اللاحقة. لما كانت العقدة
// اللاحقة هي الابن الأيسر لعقدة الأب
// دائمًا فيمكن جعل الابن الأيمن للعقدة اللاحقة
// ابنًا أيسر في العقدة الأبوية.
succParent->left = succ->right;
// نسخ بيانات العقدة اللاحقة إلى الجذر
root->key = succ->key;
// حذف العقدة اللاحقة وإعادة الجذر
delete succ;
return root;
}
}
// اختبار الدوال السابقة
int main()
{
/* لننشئ شجرة البحث الثنائية التالية
50
/ \
30 70
/ \ / \
20 40 60 80 */
Node* root = NULL;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
printf("Inorder traversal of the given tree \n");
inorder(root);
printf("\nDelete 20\n");
root = deleteNode(root, 20);
printf("Inorder traversal of the modified tree \n");
inorder(root);
printf("\nDelete 30\n");
root = deleteNode(root, 30);
printf("Inorder traversal of the modified tree \n");
inorder(root);
printf("\nDelete 50\n");
root = deleteNode(root, 50);
printf("Inorder traversal of the modified tree \n");
inorder(root);
return 0;
}
مصادر
- صفحة Binary search Trees في توثيق بنى المعطيات في موقع GeeksforGeeks.
- صفحة Binary Search Tree | Set 2 (Delete) في توثيق بنى المعطيات في موقع GeeksforGeeks.