الفرق بين المراجعتين لصفحة: «Algorithms/merge sort»
أنشأ الصفحة ب'<noinclude>{{DISPLAYTITLE:الترتيب بالدمج}}</noinclude> تقسم خوارزمية الترتيب بالدمج Merge Sort المصفوفة المدخلة إل...' |
لا ملخص تعديل |
||
| سطر 12: | سطر 12: | ||
يعرض المخطط التالي مثالًا لعمل هذه الخوارزمية: | يعرض المخطط التالي مثالًا لعمل هذه الخوارزمية: | ||
[[ملف:Merge sort algorithm diagram.svg.png|بديل=مثال يوضح خطوات خوارزمية الترتيب بالدمج|مركز|621x621بك]] | |||
يمكن ملاحظة أنّ الخوارزمية تقسم المصفوفة تعاوديًا إلى أنصاف إلى حين الوصول إلى عنصر واحد فقط، وعندها تبدأ عملية دمج الأجزاء بعضها ببعضها لنحصل على المصفوفة المرتّبة. | يمكن ملاحظة أنّ الخوارزمية تقسم المصفوفة تعاوديًا إلى أنصاف إلى حين الوصول إلى عنصر واحد فقط، وعندها تبدأ عملية دمج الأجزاء بعضها ببعضها لنحصل على المصفوفة المرتّبة. | ||
| سطر 109: | سطر 109: | ||
}</source> | }</source> | ||
يجدر الانتباه إلى أن هذه الطريقة تتطلب نفس عدد الخطوات في كل حالة، بصرف النظر عمّا إذا كانت المدخلات عشوائية أو مرتبة أو معكوسة. | يجدر الانتباه إلى أن هذه الطريقة تتطلب نفس عدد الخطوات في كل حالة، بصرف النظر عمّا إذا كانت المدخلات عشوائية أو مرتبة أو معكوسة. | ||
== تطبيقات الخوارزمية == | == تطبيقات الخوارزمية == | ||
| سطر 120: | سطر 116: | ||
# تستخدم خوارزمية الترتيب بالدمج في عمليات الترتيب الخارجي External Sorting. | # تستخدم خوارزمية الترتيب بالدمج في عمليات الترتيب الخارجي External Sorting. | ||
== | == تنفيذ الخوارزمية == | ||
تعرض الأمثلة التالية طريقة تنفيذ خوارزمية الترتيب بالدمج في عدد من لغات البرمجة: | تعرض الأمثلة التالية طريقة تنفيذ خوارزمية الترتيب بالدمج في عدد من لغات البرمجة: | ||
| سطر 383: | سطر 379: | ||
} | } | ||
} </source> | } </source> | ||
== التعقيد الزمني == | |||
يبلغ التعقيد الزمني لهذه الخوارمية المقدار <code>O(n Logn)</code> في جميع الأحوال (السيئة والمتوسطة والجيدة) وذلك لأنّ الخوارزمية تقسم المصفوفة إلى نصفين دائمًا وتستغرق وقتًا خطّيًا لدمج النصفين بعضهما ببعض. | |||
== مصادر == | == مصادر == | ||
مراجعة 22:20، 29 سبتمبر 2019
تقسم خوارزمية الترتيب بالدمج Merge Sort المصفوفة المدخلة إلى نصفين، ثم تستدعي الخوارزمية نفسها على هذين النصفين ثم تدمج نصفي المصفوفة المرتبين بعضهما ببعض.
تستخدم الدالة merge() لدمج نصفي المصفوفة بعضهما ببعض، وتعتمد الخوارزمية على هذه العملية والتي تفترض أنّ المصفوفتين arr[I..m] و arr[m+1..r] مرتبتان لتقوم بعملية الدمج.
يمكن توضيح طريقة عمل الخوارزمية بالخطوات التالية:
- إيجاد وسط المصفوفة لتقسيمها إلى نصفين.
- استدعاء الخوارزمية لنفسها على النصف الأول.
- استدعاء الخوارزمية لنفسها على النصف الثاني.
- دمج النصفين المرتبين الناتجين من الخطوتين 2 و 3.
يعرض المخطط التالي مثالًا لعمل هذه الخوارزمية:
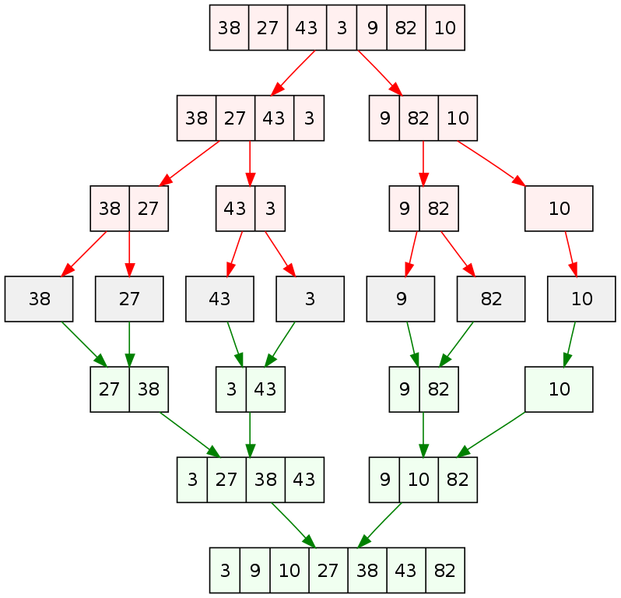
يمكن ملاحظة أنّ الخوارزمية تقسم المصفوفة تعاوديًا إلى أنصاف إلى حين الوصول إلى عنصر واحد فقط، وعندها تبدأ عملية دمج الأجزاء بعضها ببعضها لنحصل على المصفوفة المرتّبة.
دالة الدمج
تبدأ دالة الدمج عملها بتفحّص أول عنصر في كل مصفوفة فرعية وتختار القيمة الأصغر لتكون أصغر قيمة في المصفوفة كلّها. تُنقل هذه القيمة من المصفوفة الفرعية إلى المصفوفة النهائية المخرجة. وتستمر عملية الدمج بهذه الطريقة وذلك بمقارنة العناصر الأولى في المصفوفات الفرعية وإلحاق العنصر الأصغر باستمرار إلى المصفوفة النهائية المخرجة إلى حين الفراغ من جميع العناصر.
تعتمد خوارزمية الترتيب بالدمج اعتمادًا كبيرًا على دالة الدمج، وهناك عدة طرق لتنفيذ هذه الدالة منها:
الطريقة البسيطة
يُنسخ نصفا المصفوفة أولًا إلى مصفوفة مساعدة (ليكن اسمها b)، ثم يُفحص النصفان بواسطة المؤشرين i و j ويُنسخ العنصر الأكبر التالي الخاصّ بكل مؤشر إلى المصفوفة الرئيسية في كلّ مرة.
في النهاية يصل أحد المؤشرين إلى نهاية النصف الخاص به دون المؤشر الآخر، وفي هذه الحالة يجب نسخ ما تبقى من النصف غير المنتهي إلى المصفوفة الرئيسية، ولكن هذا غير ضروري في نصف المصفوفة الثاني؛ وذلك لأنّ (نسخًا من) العناصر الباقية موجودة في مكانها الصحيح أصلًا.
يعرض المثال التالي كيفية تنفيذ هذه الطريقة في لغة جافا:
void merge(int lo, int m, int hi)
{
int i, j, k;
// نسخ كلا النصفين إلى مصفوفة مساعدة
for (i=lo; i<=hi; i++)
b[i]=a[i];
i=lo; j=m+1; k=lo;
// نسخ العنصر الأكبر التالي إلى المصفوفة الرئيسية في كل دورة
while (i<=m && j<=hi)
if (b[i]<=b[j])
a[k++]=b[i++];
else
a[k++]=b[j++];
// نسخ العناصر المتبقية في النصف الأول إن وجدت
while (i<=m)
a[k++]=b[i++];
}
الطريقة الفعالة
ليس من الضروري نسخ النصف الثاني من المصفوفة a إلى المصفوفة المساعدة b، إذ يمكن لهذا النصف أن يبقى في مكانه في المصفوفة a، وبهذه الطريقة ستستهلك الخوارزمية نصف المساحة المطلوبة، وستستغرق نصف الوقت الذي تحتاجه لإجراء عملية نسخ نصف عدد العناصر من المصفوفة a إلى المصفوفة b. إضافة إلى ما سبق، إن نُسخت جميع العناصر في النصف الأولى إلى المصفوفة a فإنّ العناصر المتبقية في النصف الثانية لن تحتاج إلى التحريك لأنّها في مكانها المناسب أصلًا.
يعرض المثال التالي كيفية تنفيذ هذه الطريقة في لغة جافا:
void merge(int lo, int m, int hi)
{
int i, j, k;
i=0; j=lo;
// نسخ النصف الأول من المصفوفة الرئيسية إلى المصفوفة المساعدة
while (j<=m)
b[i++]=a[j++];
i=0; k=lo;
// نسخ العنصر الأكبر التالي إلى المصفوفة الرئيسية في كل دورة
while (k<j && j<=hi)
if (b[i]<=a[j])
a[k++]=b[i++];
else
a[k++]=a[j++];
// نسخ العناصر المتبقية في النصف الأول إن وجدت
while (k<j)
a[k++]=b[i++];
}
الطريقة ثنائية الاتجاه
يُنسخ النصف الأول من المصفوفة الرئيسية في هذه الطريقة إلى المصفوفة المساعدة حسب ورودها في المصفوفة، ولكن النصف الثاني يُنسخ بترتيب معكوس. وتكون النتيجة تسلسلًا يزداد باتجاه واحد monotonically ويتناقص باتجاه واحد، ولذلك يسمى بالتسلسل ثنائي الاتجاه bitonic sequence. بعد ذلك يُفحص هذا التسلسل بواسطة المؤشرين i و j من كلا الطرفين. وكما هو الحال في الطريقتين السابقتين، يُنسخ العنصر الأكبر التالي إلى المصفوفة الرئيسية في كل دورة من دورات الحلقة التكرارية، وتتوقف عملية النسخ عندما يتقاطع المؤشران i و j، أي عندما يصبح i > j. ويجدر الانتباه هنا إلى أنّ ليس بالضرورة أن يبقى المؤشران i و j كلّ في النصف الخاصّ به.
تعرض الشيفرة التالية كيفية تنفيذ هذه الطريقة في لغة جافا:
void merge(int lo, int m, int hi)
{
int i=lo, j=hi, k=lo;
// نسخ النصف الأول من المصفوفة الرئيسية إلى المصفوفة المساعدة
while (i<=m)
b[k++]=a[i++];
// نسخ النصف الثاني من المصفوفة الرئيسية إلى المصفوفة المساعدة
// ولكن بعكس ترتيب ورود العناصر
while (j>m)
b[k++]=a[j--];
i=lo; j=hi; k=lo;
// نسخ العنصر الأكبر التالي إلى المصفوفة الرئيسية في كل دورة
// إلى حين تقاطع المؤشرين
while (i<=j)
if (b[i]<=b[j])
a[k++]=b[i++];
else
a[k++]=b[j--];
}
يجدر الانتباه إلى أن هذه الطريقة تتطلب نفس عدد الخطوات في كل حالة، بصرف النظر عمّا إذا كانت المدخلات عشوائية أو مرتبة أو معكوسة.
تطبيقات الخوارزمية
- يمكن الاستفادة من خوارزمية الترتيب بالدمج في ترتيب القوائم المترابطة بتعقيد زمني يبلغ
O(n Logn). - مسائل العد العكسي Inversion Count
- تستخدم خوارزمية الترتيب بالدمج في عمليات الترتيب الخارجي External Sorting.
تنفيذ الخوارزمية
تعرض الأمثلة التالية طريقة تنفيذ خوارزمية الترتيب بالدمج في عدد من لغات البرمجة:
- C++:
#include<stdlib.h>
#include<stdio.h>
// تدمج الدالة المصفوفتين الناتجتين عن تقسيم المصفوفة المعطاة
// arr[l..m] المصفوفة الأولى هي
// arr[m+1..r] والمصفوفة الثانية هي
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
/* إنشاء مصفوفة مؤقتة */
int L[n1], R[n2];
/* نسخ البيانات إلى المصفوفتين المؤقتتين */
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
/* arr[l..r] دمج المصفوفتين المؤقتتين لتصبحا*/
i = 0; // الموقع الأول في المصفوفة الجزئية
j = 0; // الموقع الأول في المصفوفة الجزئية الثانية
k = l; // الموقع الأول في المصفوفة المدمجة
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
/* نسخ ما تبقى من المصفوفة الجزئية الأولى إن وجد */
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
/* نسخ ما تبقى من المصفوفة الجزئية الثانية إن وجد */
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}
/* i الموقع الأيسر
r الموقع الأيمن
للمصفوفة المجتزئة من المصفوفة الرئيسية المراد ترتبيها
*/
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
// (l+r)/2 مشابه للتعبير
// ولكنه يتجنّب حالة التحميل الزائد عندما تكون قيم
// كبيرة l و h
int m = l+(r-l)/2;
// ترتيب النصفين الأول والثاني
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}
/* دوال مساعدة */
/* دالة لطباعة محتويات المصفوفة */
void printArray(int A[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", A[i]);
printf("\n");
}
/* اختبار الدوال السابقة */
int main()
{
int arr[] = {12, 11, 13, 5, 6, 7};
int arr_size = sizeof(arr)/sizeof(arr[0]);
printf("Given array is \n");
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
printf("\nSorted array is \n");
printArray(arr, arr_size);
return 0;
}
- بايثون:
def mergeSort(arr):
if len(arr) >1:
mid = len(arr)//2 #إيجاد منتصف المصفوفة
L = arr[:mid] # تقسيم محتويات المصفوفة
R = arr[mid:] # إلى نصفين
mergeSort(L) # ترتيب النصف الأول
mergeSort(R) # ترتيب النصف الثاني
i = j = k = 0
# نسخ البيانات إلى مصفوفتين مؤقتتين
while i < len(L) and j < len(R):
if L[i] < R[j]:
arr[k] = L[i]
i+=1
else:
arr[k] = R[j]
j+=1
k+=1
# التأكد من بقاء أي عنصر في المصفوفتين المؤقتتين
while i < len(L):
arr[k] = L[i]
i+=1
k+=1
while j < len(R):
arr[k] = R[j]
j+=1
k+=1
# طباعة المصفوفة
def printList(arr):
for i in range(len(arr)):
print(arr[i],end=" ")
print()
# اختبار الدوال السابقة
if __name__ == '__main__':
arr = [12, 11, 13, 5, 6, 7]
print ("Given array is", end="\n")
printList(arr)
mergeSort(arr)
print("Sorted array is: ", end="\n")
printList(arr)
- جافا:
class MergeSort
{
// تدمج الدالة المصفوفتين الناتجتين عن تقسيم المصفوفة المعطاة
// arr[l..m] المصفوفة الأولى هي
// arr[m+1..r] والمصفوفة الثانية هي
void merge(int arr[], int l, int m, int r)
{
// إيجاد المصفوفتين الجزئيتين المراد دمجمها
int n1 = m - l + 1;
int n2 = r - m;
/* إنشاء مصفوفات مؤقتة */
int L[] = new int [n1];
int R[] = new int [n2];
/*نسخ البيانات إلى مصفوفات مؤقتة*/
for (int i=0; i<n1; ++i)
L[i] = arr[l + i];
for (int j=0; j<n2; ++j)
R[j] = arr[m + 1+ j];
/* دمج المصفوفات المؤقتة */
// المواقع الأولية للمصفوفتين الجزئيتين
int i = 0, j = 0;
// الموقع الأول في المصفوفة الجزئية المدمجة
int k = l;
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
/* نسخ ما تبقى من البيانات في المصفوفة الجزئية الأولى */
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
/* نسخ ما تبقى من البيانات في المصفوفة الجزئية الثانية */
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}
// الدالة الرئيسية التي تدمج المصفوفات باستخدام الدالة
// merge()
void sort(int arr[], int l, int r)
{
if (l < r)
{
// إيجاد نقطة المنتصف
int m = (l+r)/2;
// ترتيب النصفين الأول والثاني
sort(arr, l, m);
sort(arr , m+1, r);
// دمج النصفين المرتبين
merge(arr, l, m, r);
}
}
/* دالة مساعدة لطباعة محتويات المصفوفة */
static void printArray(int arr[])
{
int n = arr.length;
for (int i=0; i<n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
// اختبار الدوال السابقة
public static void main(String args[])
{
int arr[] = {12, 11, 13, 5, 6, 7};
System.out.println("Given Array");
printArray(arr);
MergeSort ob = new MergeSort();
ob.sort(arr, 0, arr.length-1);
System.out.println("\nSorted array");
printArray(arr);
}
}
التعقيد الزمني
يبلغ التعقيد الزمني لهذه الخوارمية المقدار O(n Logn) في جميع الأحوال (السيئة والمتوسطة والجيدة) وذلك لأنّ الخوارزمية تقسم المصفوفة إلى نصفين دائمًا وتستغرق وقتًا خطّيًا لدمج النصفين بعضهما ببعض.
مصادر
- صفحة Merge Sort في توثيق الخوارزميات في موقع GeeksforGeeks.
- موضوع Mergesort في كتاب Algorithmen in Java.