Godot/3d/using transforms

يمكن أن يكون العمل مع الدوران في الأبعاد الثلاثة مربكًا إذا لم تصمّم الألعاب ثلاثية الأبعاد من قبل، فطريقة التفكير الطبيعية عند الانتقال من العالم ثنائي الأبعاد هي: "الأمر مماثل للدوران في العالم ثنائي الأبعاد ولكن الدوران الآن يحصل في X وY وZ".

في البدء، يبدو ذلك سهلًا، وهذه الطريقة في التفكير تكون كافية للألعاب البسيطة، ولكن للأسف تكون في أغلب الحالات خاطئة.

تدعى الزوايا عادة في الأبعاد الثلاث بزوايا أويلر Euler angles.

تم تقديم زوايا أويلر من قبل الرياضي ليونارد أويلر Leonhard Euler في أوائل القرن الثامن عشر.

كانت طريقة تقديم الدورانات ثلاثية الأبعاد مبتكرة في ذلك الوقت، ولكن لها العديد من أوجه القصور عند استخدامها في تطوير الألعاب (هذا متوقع من رجل بقبعة مضحكة). هدفنا هنا هو شرح السبب بالإضافة للإشارة إلى أفضل الممارسات عند التعامل مع التحولات عند برمجة الألعاب ثلاثية الأبعاد.

المشاكل في زوايا أويلر

يمكن أن يكون من البديهي أن يكون لكل محور دوران ولكن الحقيقة أن ذلك ليس عمليًا.

ترتيب المحاور

السبب الرئيسي لذلك هو عدم وجود طريقة فريدة لبناء اتجاه من الزوايا، فلا يوجد دالة رياضية تأخذ كل الزوايا معًا وتنتج دوران ثلاثي أبعاد حقيقي. الطريقة الوحيدة للحصول على اتجاه هو تدوير كل زاوية من الكائن زاوية تلو الأخرى بترتيب عشوائي.

يمكن عمل ذلك عن طريق تدوير X ثم Y وبعدها Z. أو بطريقة أخرى يمكن تدوير Y ثم Z وأخيرًا X. أي شيء ممكن، ولكن لن يكون بالضرورة الاتجاه الأخير للكائن هو نفسه حسب الترتيب. أي يوجد عدة طرق لبناء الاتجاه من 3 زوايا مختلفة حسب ترتيب الدورانات.

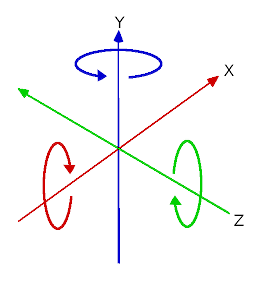
التالي هو تخيل لمحاور الدوران (بترتيب X,Y,Z) لذات المحورين gimbal، فكما ترى اتجاه كل محور يعتمد على دوران المحور السابق:

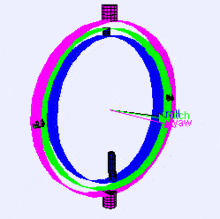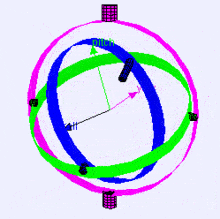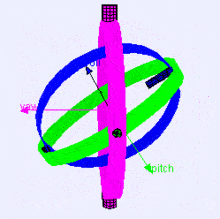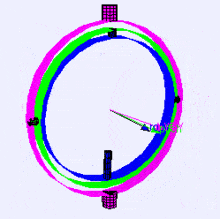
لربما تتسائل كيف سيؤثر ذلك عليك؟ لنتابع مثالًا عمليًا:

تخيل أنك تعمل على متحكم controller من المنظور الأول (أي لعبة من المنظور الأول). تتحكم حركة الفأرة لليسار واليمين بزاوية الرؤية بموازاة الأرض، وتتحكم حركة الفأرة للأعلى والأسفل برؤية اللاعب لأعلى وأسفل.

للحصول على التأثير المرغوب بهذه الحالة يجب تطبيق التدوير أولًا في المحور Y ("للأعلى" في هذه الحالة لأن جودو تستخدم الاتجاه "Y-UP")، يليها تدوير في المحور X.

سيكون التأثير غير مرغوبًا إذا طبقنا التدوير في المحور X أولًا، ومن بعدها في Y:

يمكن اختلاف ترتيب دورانات المحاور حسب التأثير المُراد إظهاره اعتمادًا على نوع اللعبة، بالتالي تطبيق التدوير في X و Y و Z غير كافي إذ عليك استخدام ترتيب للتدوير rotation order.

التوليد

مشكلة أخرى باستخدام زوايا أويلر هي التوليد interpolation. تخيل أنك تريد الانتقال بين كاميرتين مختلفتين أو لمكان العدو (متضمنًا الدوران). واحدة من الطرق المنطقية هي توليد الزوايا من مكان إلى أخر. من المتوقع أن تكون كالتالي:

لا يعطي ذلك التأثير المتوقع عند استخدام الزوايا:

تدور الكاميرا بالاتجاه المعاكس!

هناك عدة أسباب لحصول ذلك:

• لا يتطابق الدوران خطيًا مع الاتجاه، لذا التوليد لا يعطي أقصر طريق (أي الانتقال من 270 إلى 0 درجة ليس نفس الانتقال من 270 إلى 360، حتى لو كانت الزوايا متطابقة).
• تأثير قفل ذات المحورين (يتطابق دوران المحورين الأول والأخير، لذا تنقص درجة حربة). راجع صفحة ويكيبيديا عن قفل ذات المحورين لتفاصيل أكثر عن المشكلة.

قل لا لزوايا أويلر

مساعينا السابقة كانت في سبيل عدم استخدام خاصية rotation الخاصة بعقد Node3D في جودو للألعاب. هي موجودة فقط للاستخدام في المحرر بشكل أساسي للتطابق مع المحرك ثنائي الأبعاد والدورانات البسيطة (بشكل عام في محور واحد أو اثنان في حالات محدودة). على الرغم من كونها مغرية فلا تستخدمها.

هناك طريقة بديلة أفضل لحل مشكلة الدوران.

تقديم التحولات

تستخدم جودو نوع البيانات Transform3D للاتجاهات. كل عقدة Node3D تحتوي خاصية transform التي هي نسبية لتحول العقدة الأب، إذا كانت العقدة الأب مشتقة من النوع Node3D.

من الممكن الوصول إلى تحول الإحداثيات العامة عن طريق خاصية global_transform.

لدى كل تحول صنف Basis (بخاصة فرعية اسمها transform.basis) وتتكون من ثلاثة أشعة Vector3. يتم الوصول إليها عن طريق خاصية transform.basis ويمكن الوصول إليها مباشرة من خلال transform.basis.x وtransform.basis.y وtransform.basis.z. يشير كل شعاع إلى اتجاه المحور بعد التدوير أي يصف بفعالية دوران العقدة الكلي. يمكن التعرف على التدرج (إذا كان منتظم) من طول المحور. يمكن تفسير الأساس basis على أنها مصفوفة 3×3 وتستخدم transform.basis[x][y].

يشبه الأساس basis الافتراضي (غير معدل) ما يلي:

• بلغة GDScript:

var basis = Basis()
#تحتوي القيم الافتراضية التالية:
basis.x = Vector3(1, 0, 0) #شعاع على المحور ‫X
basis.y = Vector3(0, 1, 0) #شعاع على المحور ‫Y
basis.z = Vector3(0, 0, 1) #شعاع على المحور ‫Z‪‫

• بلغة C#‎:

//‎بسبب محدوديات تقنية على الهياكل في سي شارب يحتوي  الباني الافتراضي قيم الصفر لكل الحقول

var defaultBasis = new Basis();
GD.Print(defaultBasis); //يطبع: ( (0,0,0), (0,0,0) ,(0,0,0))

//يمكن استخدام خاصية الهوية عوضًا عن ذلك
var identityBasis = Basis.Identity;
GD.Print(identityBasis.X); // يطبع  (0,0,1)
GD.Print(identityBasis.Y); //يطبع  (0,1,0)
GD.Print(identityBasis.Z); //يطبع  (1,0,0)

//تساوي هوية الأساس  التالي

var basis = new Basis(Vector3.Right, Vector3.Up, Vector3.Back);

GD.Print(basis); //يطبع: ( (0,0,1), (0,1,0), (1,0,0))

هذا تشبيه أيضًا لمصفوفة هوية 3×3.

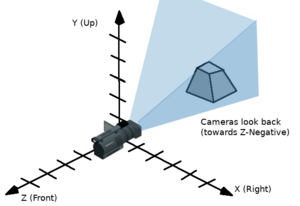
مع اتباع تحويل OpenGL يصبح X هو محور اليمين وY هو محور الأعلى وZ هو محور الأمام.

لدى التحول أيضًا مبدأ origin مع الأساس. وهو Vector3 يحدد بعد المبدأ الحقيقي (0, 0, 0) للتحول. عند دمج الأساس مع المبدأ يمكن للتحول أن يمثل بكفاءة الانتقال والدوران وحجم مميزين في الفراغ.

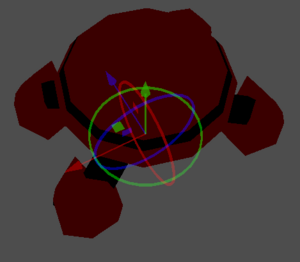
واحدة من الطرق لتخيل التحول هو للنظر إلى الأداة ثلاثية الأبعاد الخاصة بالكائن عندما يكون بوضع "الفضاء المحلي".

تظهر أسهم الأداة محاور الأساس X وY وZ (باللون الأحمر والأخضر والأزرق على الترتيب) ومركز الأداة منتصف الكائن.

اقرأ دليل رياضيات الشعاع لمزيد من المعلومات عن العمليات الرياضية المتعلقة بالأشعة والتحول.

تعديل التحولات

لا يمكن تعديل التحولات بسهولة كما هو الحال مع الزوايا، إذ لديها مشاكلها الخاصة.

من الممكن تدوير التحول إما عن طريق ضرب الأساس بأساس آخر (يدعى ذلك التراكم) أو باستخدام توابع الدوران.

• بلغة GDScript:

var axis = Vector3(1, 0, 0) # أو vector3.RIGHT

var rotation_amount = 0.1

#‫تدوير التحول حول المحور X بمقدار 0.1 راديان
transform.basis = Basis(axis, rotation_amount) * transform.basis

#تم تقصيرها
transform.basis = transform.basis.rotated(axis, rotation_amount)

• بلغة C#‎:

Vector3 axis = new Vector3(1, 0, 0); //أو vector3.RIGHT

float rotationAmount = 0.1f;

//تدوير التحول حول المحور‫ X بمقدار 0.1 راديان
transform.Basis = new Basis(axis, rotationAmount) * transform.Basis;

//تم تقصيرها
transform.Basis = transform.Basis.Rotated(axis, rotationAmount);

يمكن استخدام تابع في Node3D لتبسيط ما سبق:

• بلغة GDScript:

#تدوير التحول حول المحور‫ X بمقدار 0.1 راديان
rotate(Vector3(1, 0, 0), 0.1)

#تم تقصيرها
rotate_x(0.1)

• بلغة C‎#‎:

//تدوير التحول حول المحور‫ X بمقدار 0.1 راديان
Rotate(new Vector3(1, 0, 0), 0.1f);

//تم تقصيرها
RotateX(0.1f);

يدور ذلك العقدة بالنسبة للعقدة الأب. للتدوير النسبي لفضاء الكائن (تحول العقدة الخاص بها)، استخدم التالي:

• بلغة GDScript:

#تدوير حول المحور المحلي الخاص بالكائن بمقدار 0.1 راديان
rotate_object_local(Vector3(1, 0, 0), 0.1)

• بلغة C#‎:

//تدوير حول المحور المحلي الخاص بالكائن بمقدار 0.1 راديان
RotateObjectLocal(new Vector3(1, 0, 0), 0.1f);

أخطاء الدقة

إن القيام بالعديد من عمليات التحول سينتج بخسارة للدقة بسبب خطأ الفاصلة العشرية. هذا يعني ألا يكون تدرج كل المحاور أطول من 1.0 ولا يكون تمامًا التباعد 90 درجة من بعض.

سيتشوه المحور مع الوقت إذا تم تدوير التحول كل إطار هذا أمر لا يمكن تفاديه.

هناك طريقتان لتفادي ذلك الأولى تقويم التحول بعد بعض الوقت (ربما مرة كل إطار إذا عدلته كل إطار):

• بلغة GDScript:

transform = transform.orthonormalized()

• بلغة C#‎:

transform = transform.Orthonormalized();

هذا سيجعل المحاور بطول 1.0 وتباعد 90 درجة عن بعضها، ولكن سيزول أي تدرج تم تطبيقه على التحول.

من المحبذ عدم تغيير حجم العقد التي سيتم تعديلها، بل غير حجم العقد الأولاد بدلًا عن ذلك (مثل MeshInstance3D). إذا كنت مضطرًا لتغيير حجم العقدة فأعد التطبيق النهاية:

• بلغة GDScript:

transform = transform.orthonormalized()
transform = transform.scaled(scale)

• بلغة C#‎:

transform = transform.Orthonormalized();
transform = transform.Scaled(scale);

الحصول على المعلومات

ربما تفكر الآن:" كيف يمكنني الحصول على الزوايا من التحول؟". الجواب هو مجددا: لا يجب أن تحصل. يجب ألا تفكر بالزوايا.

تخيل أنك تريد إطلاق رصاصة في الاتجاه الذي يواجه اللاعب. استخدم فقط محور الأمام (بالعادة يكون Z أو ‎-Z).

• بلغة GDScript:

bullet.transform = transform
bullet.speed = transform.basis.z * BULLET_SPEED

• بلغة C#‎:

bullet.Transform = transform;
bullet.LinearVelocity = transform.Basis.Z * BulletSpeed;

هل يقابل العدو اللاعب؟ استخدم الضرب القياسي dot product (راجع دليل الرياضيات الشعاعية لشرح الضرب القياسي)

• بلغة GDScript:

#الحصول على شعاع الاتجاه من اللاعب إلى العدو

var direction = enemy.transform.origin - player.transform.origin
if direction.dot(enemy.transform.basis.z) > 0:
   enemy.im_watching_you(player)

• بلغة C#‎:

//الحصول على شعاع الاتجاه من اللاعب إلى العدو

Vector3 direction = enemy.Transform.Origin - player.Transform.Origin;

if (direction.Dot(enemy.Transform.Basis.Z) > 0)

{
   enemy.ImWatchingYou(player);
}

الانتقال نحو اليسار:

• بلغة GDScript:

#تذكر أن‫ +x هو اليمين

if Input.is_action_pressed("strafe_left"):
translate_object_local(-transform.basis.x)

• بلغة C#‎:

//تذكر أن‫ +x هو اليمين

if (Input.IsActionPressed("strafe_left"))

{
   TranslateObjectLocal(-Transform.Basis.X);
}

القفز:

• بلغة GDScript:

#تذكر أن‫ Y هي محور الأعلى

if Input.is_action_just_pressed("jump"):
    velocity.y = JUMP_SPEED
move_and_slide()

• بلغة C#‎:

//تذكر أن‫ Y هي محور الأعلى

if (Input.IsActionJustPressed("jump"))
   velocity.Y = JumpSpeed;

MoveAndSlide();

يمكن تطبيق المنطق والسلوك الشائعين باستخدام الأشعة فقط.

ضبط المعلومات

هناك بالطبع حالات تريد فيها ضبط المعلومات للتحول. تخيل تحكم للمنظور الأول أو كاميرا مدارية. هذه بالتأكيد مصممة باستخدام الزوايا لأنك تريد أن يحصل التحول بترتيب معين.

حافظ على الزوايا والدورانات خارج التحول لهذه الحالات واضبطهم كل إطار. لا تحاول استعادتهم وإعادة استخدامهم لأن التحول لا يُعمل بهذه الطريقة.

أمثلة للتجوال في النظر بنمط منظور الشخص الأول:

• بلغة GDScript:

#المراكمات

var rot_x = 0
var rot_y = 0

func _input(event):

    if event is InputEventMouseMotion and event.button_mask & 1:
        #تعديل دورانات الفأرة المتراكمة
        rot_x += event.relative.x * LOOKAROUND_SPEED
        rot_y += event.relative.y * LOOKAROUND_SPEED
        transform.basis = Basis() # إعادة ضبط الدوران
        rotate_object_local(Vector3(0, 1, 0), rot_x) # الدوران حول‫ Y أولًا
        rotate_object_local(Vector3(1, 0, 0), rot_y) # ثم الدوران حول‫ X

• بلغة C#‎:

//المراكمات

private float _rotationX = 0f;
private float _rotationY = 0f;

public override void _Input(InputEvent @event)
{
   if (@event is InputEventMouseMotion mouseMotion)

   {
// تعديل دورانات الفأرة المتراكمة
       _rotationX += mouseMotion.Relative.X * LookAroundSpeed;
       _rotationY += mouseMotion.Relative.Y * LookAroundSpeed;

//إعادة ضبط الدوران
       Transform3D transform = Transform;
       transform.Basis = Basis.Identity;
       Transform = transform;
       RotateObjectLocal(Vector3.Up, _rotationX); // الدوران أولًا حول‫ Y
       RotateObjectLocal(Vector3.Right, _rotationY); // ثم الدوران حول‫ X
   }

}

كما نرى في هذه الحالات أنه من الأسهل إبقاء الدوران في الخارج ثم استخدام التحول في الاتجاه الأخير.

التوليد باستخدام الرباعيات

يمكن التوليد بين تحولين بكفاءة باستخدام الرباعيات quaternions. يمكن إيجاد معلومات أكثر عن كيفية عمل الرباعيات في أماكن أخرى على الإنترنت. من الكافي معرفة أن استخدامهم الأساسي هو توليد أقرب طريق. إذا كان لدينا دورانين يسمح الرباعي بالتوليد بين الدورانين باستخدام المحور الأقرب.

إن تحويل الدوران إلى رباعي هو عملية واضحة.

• بلغة GDScript:

#تحويل الأساس إلى رباعي، تذكر أن الحجم سيزول
var a = Quaternion(transform.basis)
var b = Quaternion(transform2.basis)

#التوليد باستخدام التوليد الكروي الخطي‫ (SLERP)
var c = a.slerp(b,0.5) #أوجد النقطة الوسطى بين‫ a و b

#طبق الرجوع
transform.basis = Basis(c)

• بلغة C#‎:

//تحويل الأساس إلى رباعي تذكر أن تغيير الحجم سيزول
var a = transform.Basis.GetQuaternion();
var b = transform2.Basis.GetQuaternion();

//‫التوليد باستخدام التوليد الكروي الخطي (SLERP)
var c = a.Slerp(b, 0.5f);  //‫أوجد النقطة الوسطى بين a و b

//طبق الرجوع
transform.Basis = new Basis(c);

يشير نوع المرجع Quaternion إلى معلومات أكثر عن نوع البيانات (يمكنه أيضًا القيام بتراكم التحول ونقاط التحول إلخ ولكن ذلك لا يستخدم كثيرًا) إذا كنت بحاجة توليد أو تطبق العمليات على الرباعيات عدد من المرات فيجب تطبيعهم في النهاية، وإلا سيكون هناك أخطاء دقة رقمية.

تفيد الرباعيات عند توليد للكاميرا/مسار/إلخ ،إذ ستكون النتائج صحيحة وسلسلة.

التحولات هي صديقتك

إن العمل مع التحولات قد يستغرق وقتًا للمبتدئين، ولكن عندما تعتاد عليهم ستقدّر بساطتهم وقوتهم.

لا تتردد في طلب المساعدة عن هذا الموضوع في أي من مجتمعات جودو على الويب وعندما تصبح ذا معرفة من فضلك ساعد الآخرين.

مصادر

• صفحة Using Transforms في توثيق جودو الرسمي.