الكشف عن وجود دورة في الرسم البياني

الهدف من هذه الخوارزمية هو الكشف عن وجود دورة في الرسم البياني الموجّه. فعلى سبيل المثال يحتوي الرسم البياني التالي على ثلاثة دورات هي ‎0->2->0 و ‎0->1->2->0 و ‎3->3.

يمكن استخدام عملية البحث بالعمق أولًا Depth First Search للكشف عن وجود دورة في الرسم البياني. تنتج عملية البحث بالعمق أولًا شجرة عند إجرائها على الرسم البياني المتصل.

يحتوي الرسم البياني على دورة إذا كان يحتوي على ضلع خلفي back edge، والمقصود بالضلع الخلفي الضلع الذي يخرج من العقدة ويعود إليها (حلقة-ذاتية) أو إلى أحد أسلافها في الشجرة الناتجة من عملية البحث بالعمق أولًا.

يحتوي الرسم البياني التالي على ثلاثة أضلاع خلفية معلمة بعلامة x.

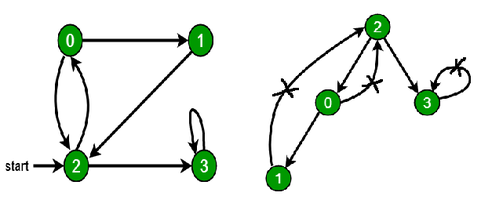
يمكن ملاحظة أن وجود ثلاثة أضلاع خلفية في الرسم البياني يشير إلى وجود ثلاث دورات فيه.

أما في حالة الرسم البياني غير المتصل disconnected فإن النتيجة هي مجموعة من الأشجار التي تعرف بغابة DFS Forest، وللكشف عن وجود الدورات يمكن التحقق من وجود الأضلاع الخلفية في كل شجرة على حدة.

للتحقق من وجود الضلع الخلفي يمكن متابعة الرؤوس الموجودة كدس التعاود recursion stack الخاص بالدالة في عملية التنقل بالعمق أولًا. فإن وصلنا إلى رأس موجود فعلًا في مكدس التعاود، فهذا يعني أنّ الشجرة تحتوي على دورة. إن الضلع الذي يربط العقدة الحالية بالعقدة الموجودة في مكدس التعاود هو ضلع خلفي.

أمثلة

تعرض الأمثلة التالية طريقة تنفيذ هذه الخوارزمية في عدد من لغات البرمجة:

• C++‎:

#include<iostream> 
#include <list> 
#include <limits.h> 

using namespace std; 

class Graph 
{ 
	int V; // عدد الرؤوس
	list<int> *adj; // مؤشر إلى مصفوفة تحتوي على قوائم المجاورة 
	bool isCyclicUtil(int v, bool visited[], bool *rs); // isCyclic() تستخدم هذه الدالة من قبل الدالة
public: 
	Graph(int V); // إنشاء كائن الرسم البياني 
	void addEdge(int v, int w); // إضافة ضلع إلى الرسم البياني
	bool isCyclic(); // تعيد الدالة قيمة صحيحة عند وجود دورة في الرسم البياني
}; 

Graph::Graph(int V) 
{ 
	this->V = V; 
	adj = new list<int>[V]; 
} 

void Graph::addEdge(int v, int w) 
{ 
	adj[v].push_back(w); // إضافة الضلع المعطى 
} 


bool Graph::isCyclicUtil(int v, bool visited[], bool *recStack) 
{ 
	if(visited[v] == false) 
	{ 
		// تعليم العقدة المعطاة على أنّها مزورة وأنّها في مكدس التعاود
		visited[v] = true; 
		recStack[v] = true; 

		// تنفيذ الدالة تعاوديًا على جميع الرؤوس المجاورة
		list<int>::iterator i; 
		for(i = adj[v].begin(); i != adj[v].end(); ++i) 
		{ 
			if ( !visited[*i] && isCyclicUtil(*i, visited, recStack) ) 
				return true; 
			else if (recStack[*i]) 
				return true; 
		} 

	} 
	recStack[v] = false; // حذف الرأس من مكدس التعاود
	return false; 
} 

// تعيد الدالة قيمة صحيحة إن احتوى الرسم البياني على دورة وإلا فإنّها تعيد قيمة خاطئة
bool Graph::isCyclic() 
{ 
	// تعليم العقدة المعطاة على أنّها غير مزورة وأنّها ليست في مكدس التعاود 
	bool *visited = new bool[V]; 
	bool *recStack = new bool[V]; 
	for(int i = 0; i < V; i++) 
	{ 
		visited[i] = false; 
		recStack[i] = false; 
	} 

	// استدعاء الدالة التعاودية المساعدة للكشف عن وجود الدورة في أشجار مختلفة
	for(int i = 0; i < V; i++) 
		if (isCyclicUtil(i, visited, recStack)) 
			return true; 

	return false; 
} 

int main() 
{ 
	// إنشاء الرسم البياني في أعلاه
	Graph g(4); 
	g.addEdge(0, 1); 
	g.addEdge(0, 2); 
	g.addEdge(1, 2); 
	g.addEdge(2, 0); 
	g.addEdge(2, 3); 
	g.addEdge(3, 3); 

	if(g.isCyclic()) 
		cout << "Graph contains cycle"; 
	else
		cout << "Graph doesn't contain cycle"; 
	return 0; 
}

• بايثون:

from collections import defaultdict 

class Graph(): 
	def __init__(self,vertices): 
		self.graph = defaultdict(list) 
		self.V = vertices 

	def addEdge(self,u,v): 
		self.graph[u].append(v) 

	def isCyclicUtil(self, v, visited, recStack): 

		# تعليم العقدة الحالية على أنّها مزورة
		# وإضافتها إلى مكدس التعاود
		visited[v] = True
		recStack[v] = True

		# تنفيذ الدالة تعاوديًا على جميع العقد المجاورة
		# إن كانت العقدة المجاورة مزورة وموجودة في
		# مكدس التعاود فهذا يعني وجود دورة في الرسم البياني
		for neighbour in self.graph[v]: 
			if visited[neighbour] == False: 
				if self.isCyclicUtil(neighbour, visited, recStack) == True: 
					return True
			elif recStack[neighbour] == True: 
				return True

		# يجب إزالة العقدة من مكدس التعاود
		# قبل إنهاء عمل الدالة
		recStack[v] = False
		return False

	# تعيد الدالة قيمة صحيحة في حال وجود دورة في الرسم البياني
	def isCyclic(self): 
		visited = [False] * self.V 
		recStack = [False] * self.V 
		for node in range(self.V): 
			if visited[node] == False: 
				if self.isCyclicUtil(node,visited,recStack) == True: 
					return True
		return False

g = Graph(4) 
g.addEdge(0, 1) 
g.addEdge(0, 2) 
g.addEdge(1, 2) 
g.addEdge(2, 0) 
g.addEdge(2, 3) 
g.addEdge(3, 3) 
if g.isCyclic() == 1: 
	print "Graph has a cycle"
else: 
	print "Graph has no cycle"

• جافا:

import java.util.ArrayList; 
import java.util.LinkedList; 
import java.util.List; 

class Graph { 
	
	private final int V; 
	private final List<List<Integer>> adj; 

	public Graph(int V) 
	{ 
		this.V = V; 
		adj = new ArrayList<>(V); 
		
		for (int i = 0; i < V; i++) 
			adj.add(new LinkedList<>()); 
	} 
	
	
	private boolean isCyclicUtil(int i, boolean[] visited, 
									boolean[] recStack) 
	{ 
		
		// تعليم العقدة الحالية على أنّها مزورة
		// وإضافتها إلى مكدس التعاود
		if (recStack[i]) 
			return true; 

		if (visited[i]) 
			return false; 
			
		visited[i] = true; 

		recStack[i] = true; 
		List<Integer> children = adj.get(i); 
		
		for (Integer c: children) 
			if (isCyclicUtil(c, visited, recStack)) 
				return true; 
				
		recStack[i] = false; 

		return false; 
	} 

	private void addEdge(int source, int dest) { 
		adj.get(source).add(dest); 
	} 

	// تعيد الدالة قيمة صحيحة في حال وجود دورة في الرسم البياني
	private boolean isCyclic() 
	{ 
		
		// تعليم جميع الرؤوس على أنّها غير مزورة
		// وأنّها ليست جزءًا من مكدس التعاود
		boolean[] visited = new boolean[V]; 
		boolean[] recStack = new boolean[V]; 
		
		
		// استدعاء الدالة التعاودية المساعدة للكشف عن وجود الدورة في أشجار مختلفة 
		for (int i = 0; i < V; i++) 
			if (isCyclicUtil(i, visited, recStack)) 
				return true; 

		return false; 
	} 

	// اختبار التوابع السابقة
	public static void main(String[] args) 
	{ 
		Graph graph = new Graph(4); 
		graph.addEdge(0, 1); 
		graph.addEdge(0, 2); 
		graph.addEdge(1, 2); 
		graph.addEdge(2, 0); 
		graph.addEdge(2, 3); 
		graph.addEdge(3, 3); 
		
		if(graph.isCyclic()) 
			System.out.println("Graph contains cycle"); 
		else
			System.out.println("Graph doesn't "
									+ "contain cycle"); 
	} 
}

التعقيد الزمني

التعقيد الزمني لهذه العملية مشابه للتعقيد الزمني لعملية البحث بالعمق أولًا وهي O(V+E)‎.

مصادر

• صفحة Detect Cycle in a Directed Graph في توثيق الخوارزميات في موقع GeeksforGeeks.