الترتيب بالإدراج
الترتيب بالإدراج Insertion Sort من خوارزميات الترتيب البسيطة التي تعمل بنفس الطريقة التي ترتّب فيها أوراق اللعب يدويًّا.
يعرض الشكل التالي مثالًا عن طريقة عمل خوارزمية الترتيب بالإدراج:
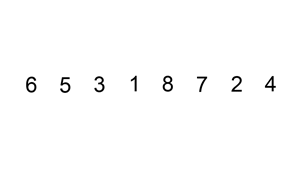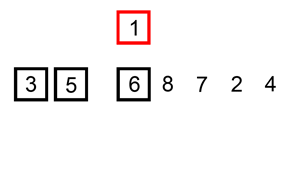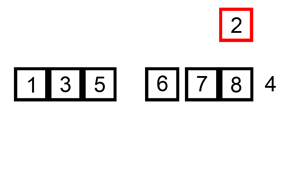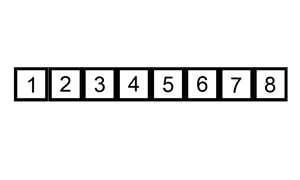
لنفترض أنّ لدينا المصفوفة التالية:
12, 11, 13, 5, 6
عند الانتقال عبر المصفوفة من العنصر i = 1 (العنصر الثاني في المصفوفة) إلى i = 4 (العنصر الأخير في المصفوفة). لمّا كانت 11 اصغر من 12، نحرّك 12 وندرج 11 قبلها.
11, 12, 13, 5, 6
تبقى 13 في مكانها وذلك لأنّ جميع العناصر التي قبلها أصغر منها.
11, 12, 13, 5, 6
تنتقل 5 إلى بداية المصفوفة وتتحرك بقية العناصر (11 إلى 13) موقعًا واحدًا إلى الأمام.
5, 11, 12, 13, 6
تنتقل 6 إلى الموقع الذي يلي 5، وتتحرّك بقية العناصر (11 إلى 13) موقعًا واحدًا إلى الأمام.
5, 6, 11, 12, 13
تستخدم خوارزمية الترتيب بالإدراج عند التعامل مع عدد قليل من الأرقام، ويمكن لهذه الخوارزمية أن تكون مفيدة عندما تكون المصفوفة المدخلة مرتّبة تقريبًا. وتتبع هذه الخوارزمية الأسلوب التصاعدي Incremental.
تنفيذ الخوارزمية
يمكن تنفيذ خوارزمية الترتيب بالإدراج بطريقتين هما التكرارية والتعاودية:
الطريقة التكرارية
تعرض الأمثلة التالية طريقة تنفيذ خوارزمية الترتيب بالإدراج في عدد من لغات البرمجة:
- C++:
#include <bits/stdc++.h>
using namespace std;
void insertionSort(int arr[], int n)
{
int i, key, j;
for (i = 1; i < n; i++)
{
key = arr[i];
j = i - 1;
/* تحريك العناصر في المصفوفة
arr[0..i-1]
والتي تكون أكبر من المفتاح المعطى
بمقدار موقع واحد عن موقعها الحالي
*/
while (j >= 0 && arr[j] > key)
{
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// دالة مساعدة لطباعة محتويات المصفوفة
void printArray(int arr[], int n)
{
int i;
for (i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
}
/* اختبار الدالة السابقة */
int main()
{
int arr[] = { 12, 11, 13, 5, 6 };
int n = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, n);
printArray(arr, n);
return 0;
}
- بايثون:
def insertionSort(arr):
# التنقل عبر عناصر المصفوفة من الموقع 1 إلى نهاية المصفوفة
for i in range(1, len(arr)):
key = arr[i]
# تحريك العناصر في المصفوفة
# arr[0..i-1]
# والتي تكون أكبر من المفتاح المعطى
# بمقدار موقع واحد عن موقعها الحالي
j = i-1
while j >= 0 and key < arr[j] :
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
# اختبار الدالة السابقة
arr = [12, 11, 13, 5, 6]
insertionSort(arr)
for i in range(len(arr)):
print ("% d" % arr[i])
- جافا:
class InsertionSort {
void sort(int arr[])
{
int n = arr.length;
for (int i = 1; i < n; ++i) {
int key = arr[i];
int j = i - 1;
/* تحريك العناصر في المصفوفة
arr[0..i-1]
والتي تكون أكبر من المفتاح المعطى
بمقدار موقع واحد عن موقعها الحالي
*/
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
/* دالة مساعدة لطباعة محتويات المصفوفة */
static void printArray(int arr[])
{
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
// اختبار الدوال السابقة
public static void main(String args[])
{
int arr[] = { 12, 11, 13, 5, 6 };
InsertionSort ob = new InsertionSort();
ob.sort(arr);
printArray(arr);
}
}
الطريقة التعاودية
لا تمتلك الطريقة التعاودية أي ميزة من ناحية التنفيذ أو الأداء مقارنة بالطريقة التكرارية.
تشمل الطريقة التعاودية الخطوات التالية:
- الحالة الأساس: إن كان حجم المصفوفة 1 أو أقل، تتوقف الدالة عن العمل.
- ترتيب أول العناصر التي تحمل القيمة
n-1تعاوديًا. - إدراج العنصر الأخير في موقعه الصحيح ضمن المصفوفة المرتبة.
تعرض الأمثلة التالية طريقة تنفيذ هذه الخوارزمية في عدد من لغات البرمجة بالطريقة التعاودية:
- C++:
#include <iostream>
using namespace std;
void insertionSortRecursive(int arr[], int n)
{
// الحالة الأساس
if (n <= 1)
return;
// n-1 ترتيب أول العناصر التي تحمل القيمة
insertionSortRecursive( arr, n-1 );
// إدراج العنصر الأخير في مكانه الصحيح ضمن المصفوفة المرتبة
int last = arr[n-1];
int j = n-2;
/* تحريك العناصر في المصفوفة
arr[0..i-1]
والتي تكون أكبر من المفتاح المعطى
بمقدار موقع واحد عن موقعها الحالي
*/
while (j >= 0 && arr[j] > last)
{
arr[j+1] = arr[j];
j--;
}
arr[j+1] = last;
}
// دالة مساعدة لطباعة محتويات المصفوفة
void printArray(int arr[], int n)
{
for (int i=0; i < n; i++)
cout << arr[i] <<" ";
}
/* اختبار الدوال السابقة */
int main()
{
int arr[] = {12, 11, 13, 5, 6};
int n = sizeof(arr)/sizeof(arr[0]);
insertionSortRecursive(arr, n);
printArray(arr, n);
return 0;
}
- بايثون:
def insertionSortRecursive(arr,n):
# الحالة الأساس
if n<=1:
return
# n-1 ترتيب أول العناصر التي تحمل القيمة
insertionSortRecursive(arr,n-1)
# إدراج العنصر الأخير في موقعه الصحيح ضمن المصفوفة المرتبة
last = arr[n-1]
j = n-2
# تحريك العناصر في المصفوفة
# arr[0..i-1]
# والتي تكون أكبر من المفتاح المعطى
# بمقدار موقع واحد عن موقعها الحالي
while (j>=0 and arr[j]>last):
arr[j+1] = arr[j]
j = j-1
arr[j+1]=last
# دالة مساعدة لطباعة محتويات المصفوفة
def printArray(arr,n):
for i in range(n):
print arr[i],
# اختبار الدوال السابقة
arr = [12,11,13,5,6]
n = len(arr)
insertionSortRecursive(arr, n)
printArray(arr, n)
- جافا:
import java.util.Arrays;
public class GFG
{
static void insertionSortRecursive(int arr[], int n)
{
// الحالة الأساس
if (n <= 1)
return;
// n-1 ترتيب أول العناصر التي تحمل القيمة
insertionSortRecursive( arr, n-1 );
// إدراج العنصر الأخير في مكانه الصحيح ضمن المصفوفة المرتبة
int last = arr[n-1];
int j = n-2;
/* تحريك العناصر في المصفوفة
arr[0..i-1]
والتي تكون أكبر من المفتاح المعطى
بمقدار موقع واحد عن موقعها الحالي
*/
while (j >= 0 && arr[j] > last)
{
arr[j+1] = arr[j];
j--;
}
arr[j+1] = last;
}
// اختبار الدوال السابقة
public static void main(String[] args)
{
int arr[] = {12, 11, 13, 5, 6};
insertionSortRecursive(arr, arr.length);
System.out.println(Arrays.toString(arr));
}
}
خوارزمية البحث بالإدراج الثنائي
يمكن استخدام عملية البحث الثنائي Binary Search لتقليل عدد المقارنات المعقودة في خوارزمية الترتيب بالإدراج الاعتيادية. تستخدم خوارزمية الترتيب بالإدراج الثنائي Binary Insertion Sort البحث الثنائي للعثور على الموقع المناسب لإدراج العنصر المحدّد في كل دورة. يبلغ التعقيد الزمني لعملية الإدارج الاعتيادية O(i) (عند الدورة i) في أسوأ الحالات، ولكن يمكن تخفيض هذا المقدار ليصبح O(Log i) باستخدام خوارزمية البحث الثنائي.
غير أنّ التعقيد الزمني لهذه العملية في أسوأ الحالات يبقى O(n^2) وذلك بسبب سلسلة التبديلات المطلوبة في كل دورة.
- C++:
#include <stdio.h>
int binarySearch(int a[], int item, int low, int high)
{
if (high <= low)
return (item > a[low])? (low + 1): low;
int mid = (low + high)/2;
if(item == a[mid])
return mid+1;
if(item > a[mid])
return binarySearch(a, item, mid+1, high);
return binarySearch(a, item, low, mid-1);
}
void insertionSort(int a[], int n)
{
int i, loc, j, k, selected;
for (i = 1; i < n; ++i)
{
j = i - 1;
selected = a[i];
// إيجاد الموقع الذي سيُدرج فيه العنصر المحدد
loc = binarySearch(a, selected, 0, j);
// تحريك جميع العناصر التي تلي الموقع
while (j >= loc)
{
a[j+1] = a[j];
j--;
}
a[j+1] = selected;
}
}
// اختبار الدوال السابقة
int main()
{
int a[] = {37, 23, 0, 17, 12, 72, 31,
46, 100, 88, 54};
int n = sizeof(a)/sizeof(a[0]), i;
insertionSort(a, n);
printf("Sorted array: \n");
for (i = 0; i < n; i++)
printf("%d ",a[i]);
return 0;
}
- بايثون:
def binary_search(arr, val, start, end):
# يجب معرفة المكان الذي سندرج العنصر فيه
# قبل أو بعد الحد الأيسر
if start == end:
if arr[start] > val:
return start
else:
return start+1
# تحدث هذه الحالة إن كنا ننتقل إلى ما وراء الحد الأيسر
# ما يعني أنّ الحد الأيسر هو أقل موقع يمكن
# أن نعثر فيه على رقم أكبر من القيمة المعطاة
if start > end:
return start
mid = (start+end)/2
if arr[mid] < val:
return binary_search(arr, val, mid+1, end)
elif arr[mid] > val:
return binary_search(arr, val, start, mid-1)
else:
return mid
def insertion_sort(arr):
for i in xrange(1, len(arr)):
val = arr[i]
j = binary_search(arr, val, 0, i-1)
arr = arr[:j] + [val] + arr[j:i] + arr[i+1:]
return arr
print("Sorted array:")
print insertion_sort([37, 23, 0, 17, 12, 72, 31,
46, 100, 88, 54])
- جافا:
import java.util.Arrays;
class GFG
{
public static void main(String[] args)
{
final int[] arr = {37, 23, 0, 17, 12, 72, 31,
46, 100, 88, 54 };
new GFG().sort(arr);
for(int i=0; i<arr.length; i++)
System.out.print(arr[i]+" ");
}
public void sort(int array[])
{
for (int i = 1; i < array.length; i++)
{
int x = array[i];
// العثور على موقع إدراج العنصر باستخدام البحث الثنائي
int j = Math.abs(Arrays.binarySearch(array, 0, i, x) + 1);
// تحريك عناصر المصفوفة موقعًا واحدًا إلى اليمين
//Shifting array to one location right
System.arraycopy(array, j, array, j+1, i-j);
//وضع العنصر في موقعه الصحيح
array[j] = x;
}
}
}
التعقيد الزمني
يبلغ التعقيد الزمني لهذه الخوارزمية المقدار O(n*2).
تبلغ هذه الخوارزمية تعقيدها الزمني الأقصى عندما تكون العناصر مرتّبة ترتيبًا عكسيًا، وتبلغ تعقيدها الأدنى عندما تكون العناصر مرتّبة أصلًا.
مصادر
- صفحة Insertion Sort في توثيق الخوارزميات في موقع GeeksforGeeks.
- صفحة Binary Insertion Sort في توثيق الخوارزميات في موقع GeeksforGeeks.