الترتيب بالتحديد

مثال توضيحي لطريقة عمل خوارزمية الترتيب بالتحديد. المصدر: ويكيبديا

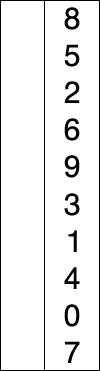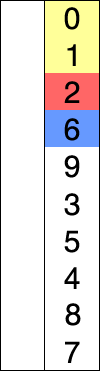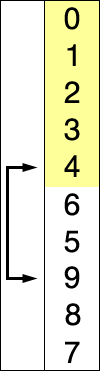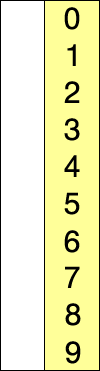
ترتّب خوارزمية الترتيب بالتحديد selection sort المصفوفة عن طريق العثور على أصغر عنصر (بافتراض أنّ الترتيب سيكون ترتيبًا تصاعديًا) في الجزء غير المرتّب من المصفوفة ووضعه في بدايتها.

تتعامل الخوارزمية مع مصفوفتين جزئيتين في المصفوفة الأصلية:

1. المصفوفة الجزئية المرتّبة.
2. المصفوفة الجزئية المتبقية والتي تكون غير مرتّبة.

في كل دورة من دورات خوارزمية الترتيب بالتحديد، يؤخذ العنصر ذو القيمة الأصغر (بافتراض الترتيب التصاعدي) من الجزء غير المرتّب ويوضع في الجزء المرتّب من المصفوفة.

تنفيذ الخوارزمية

تعرض الأمثلة التالية طريقة تنفيذ خوارزمية الترتيب بالتحديد في عدد من لغات البرمجة:

• C++‎:

#include <bits/stdc++.h> 
using namespace std; 

void swap(int *xp, int *yp) 
{ 
	int temp = *xp; 
	*xp = *yp; 
	*yp = temp; 
} 

void selectionSort(int arr[], int n) 
{ 
	int i, j, min_idx; 

	// التحرك ضمن المصفوفة غير المرتبة خطوة بخطوة
	for (i = 0; i < n-1; i++) 
	{ 
		// العثور على أصغر عنصر في المصفوفة غير المرتبة
		min_idx = i; 
		for (j = i+1; j < n; j++) 
		if (arr[j] < arr[min_idx]) 
			min_idx = j; 

		// تبديل موقع العنصر الذي عثر عليه مع العنصر الأول في المصفوفة
		swap(&arr[min_idx], &arr[i]); 
	} 
} 

/* دالة لطباعة المصفوفة */
void printArray(int arr[], int size) 
{ 
	int i; 
	for (i=0; i < size; i++) 
		cout << arr[i] << " "; 
	cout << endl; 
} 

// اختبار الدوال السابقة
int main() 
{ 
	int arr[] = {64, 25, 12, 22, 11}; 
	int n = sizeof(arr)/sizeof(arr[0]); 
	selectionSort(arr, n); 
	cout << "Sorted array: \n"; 
	printArray(arr, n); 
	return 0; 
}

• بايثون:

import sys 
A = [64, 25, 12, 22, 11] 

# التنقل عبر جميع عناصر القائمة
for i in range(len(A)): 
	
	# العثور على أصغر عنصر في المصفوفة غير المرتبة
	min_idx = i 
	for j in range(i+1, len(A)): 
		if A[min_idx] > A[j]: 
			min_idx = j 
			
	# تبديل موقع العنصر الذي عُثر عليه مع العنصر الأول
	A[i], A[min_idx] = A[min_idx], A[i] 

# اختبار الدالة السابقة
print ("Sorted array") 
for i in range(len(A)): 
	print("%d" %A[i]),

• جافا:

class SelectionSort 
{ 
	void sort(int arr[]) 
	{ 
		int n = arr.length; 

		// التحرك ضمن المصفوفة غير المرتبة خطوة بخطوة
		for (int i = 0; i < n-1; i++) 
		{ 
			// العثور على أصغر عنصر في المصفوفة غير المرتبة
			int min_idx = i; 
			for (int j = i+1; j < n; j++) 
				if (arr[j] < arr[min_idx]) 
					min_idx = j; 

			// تبديل موقع العنصر الذي عثر عليه مع العنصر الأول في المصفوفة
			int temp = arr[min_idx]; 
			arr[min_idx] = arr[i]; 
			arr[i] = temp; 
		} 
	} 

	// طباعة المصفوفة
	void printArray(int arr[]) 
	{ 
		int n = arr.length; 
		for (int i=0; i<n; ++i) 
			System.out.print(arr[i]+" "); 
		System.out.println(); 
	} 

	// اختبار الدوال السابقة
	public static void main(String args[]) 
	{ 
		SelectionSort ob = new SelectionSort(); 
		int arr[] = {64,25,12,22,11}; 
		ob.sort(arr); 
		System.out.println("Sorted array"); 
		ob.printArray(arr); 
	} 
}

تعطي الشيفرات السابقة المخرجات التالية:

Sorted array: 
11 12 22 25 64

التعقيد الزمني

يبلغ التعقيد الزمني لهذه الخوارزمية O(n^2)‎ وذلك لوجود حلقتين تكراريتين متداخلتين.

مصادر

• صفحة Selection Sort في توثيق الخوارزميات في موقع GeeksforGeeks.