المكادس

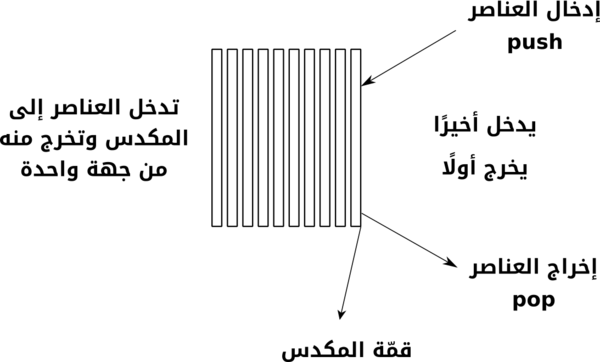
المكدس هو من بنى المعطيات الخطية والذي يتبع طريقتين في ترتيب أداء العمليات هما LIFO (يدخل آخرًا ويخرج أولًا Last In First Out) أو FILO (يدخل أولًا ويخرج آخرًا First In Last Out).

يمكن تأدية العمليات التالية بصورة رئيسية على المكادس:

• الإضافة Push: إضافة عنصر إلى المكدس، وإن كان المكدس ممتلئًا، فتُسمى الحالة حينئذٍ بالفيض أو تجاوز السعة overflow.
• الحذف Pop: تحذف العناصر من المكدس بعكس الترتيب الذي دخلت فيه إلى المكدس، وإن كان المكدس فارغًا فتُسمّى الحالة حينئذٍ بالغيض underflow.
• القمة Peek or Top: تعيد هذه العملية العنصر الموجود في قمّة المكدس.
• isEmpty: تعيد هذه العملية قيمة صحيحة إن كان المكدس فارغًا، وتعيد قيمة خاطئة فيما عدا ذلك.

مثال عملي على المكادس

هناك الكثير من الأمثلة العملية في الحياة اليومية والتي يمكن الاستفادة منها في فهم آلية عمل الأكداس. فعلى سبيل المثال يمكن وضع مجموعة من الأطباق فوق بعضها البعض لتشكّل بذلك مكدسًا يكون فيه الطبق الأعلى أوّل طبق يمكن إزالته من المكدس، وهذا يعني أن الطبق الأخير (الأسفل) في هذا المكدس سيبقى فيه لأطول فترة من الوقت، ويمكن القول أنّ هذه الأطباق تتبع الترتيب LIFO/FILO.

التعقيد الزمني الخاصّ بهذه العمليات

تستغرق العمليات push()‎ و pop()‎ و isEmpty()‎ و peek()‎ الوقت O(1)‎ وذلك لعدم استخدام أيّ حلقة تكرارية في هذه العمليات.

تطبيقات على الأكداس

• موازنة الرموز Balancing of symbols
• تحويل Infix إلى Postfix / تحويل Prefix
• عمليات الإعادة والتراجع في الكثير من البرامج مثل محررات النصوص والفوتوشوب.
• خاصية عرض الصفحات اللاحقة والسابقة في متصفحات الويب.
• تستخدم الأكداس في كثير من الخوارزميات مثل برج هانوي  Tower of Hanoi، والتنقل في الشجرة Tree Traversals، وفي مسألة المدرج التكراري histogram.
• تطبيقات أخرى مثل التعقب الخلفي backtracking، ومسألة جولة الفارس Knight tour، والفأر في المتاهة rat in a maze، وحل لعبة السودوكو sudoku.
• في خوارزميات الصور مثل الترتيب الطوبولوجي والمكونات المرتبطة بقوة Strongly Connected Components.

تنفيذ المكادس

يمكن تنفيذ المكادس بطريقتين:

• باستخدام المصفوفات.
• باستخدام القوائم المترابطة.

تنفيذ المكادس باستخدام المصفوفات

تعرض الأمثلة التالية طرق إنشاء الأكداس باستخدام المصفوفات وفي عدد من لغات البرمجة:

• C++‎:

#include<bits/stdc++.h> 
  
using namespace std; 
  
#define MAX 1000 
  
class Stack 
{ 
    int top; 
public: 
    int a[MAX];    //تعيين الحد الأعلى للكدس 
  
    Stack()  { top = -1; } 
    bool push(int x); 
    int pop(); 
    bool isEmpty(); 
}; 
  
bool Stack::push(int x) 
{ 
    if (top >= (MAX-1)) 
    { 
        cout << "Stack Overflow"; 
        return false; 
    } 
    else
    { 
        a[++top] = x; 
        cout<<x <<" pushed into stack\n"; 
        return true; 
    } 
} 
  
int Stack::pop() 
{ 
    if (top < 0) 
    { 
        cout << "Stack Underflow"; 
        return 0; 
    } 
    else
    { 
        int x = a[top--]; 
        return x; 
    } 
} 
  
bool Stack::isEmpty() 
{ 
    return (top < 0); 
} 
  
// اختبار الدوال السابقة 
int main() 
{ 
    class Stack s; 
    s.push(10); 
    s.push(20); 
    s.push(30); 
    cout<<s.pop() << " Popped from stack\n"; 
  
    return 0; 
}

• بايثون:

تحتاج الشيفرة إلى استيراد المتغير maxsize من الوحدة sys وذلك لإعادة القيمة ‎-infinite‎ إن كان المكدس فارغًا:

from sys import maxsize 

# دالة لإنشاء المكدس وتهيئته ليكون بحجم 0
def createStack(): 
	stack = [] 
	return stack 

# يكون المكدس فارغًا عندما يكون حجمه صفرًا
def isEmpty(stack): 
	return len(stack) == 0

# دالة لإضافة عنصر إلى المكدس، وزيادة حجم المكدس بمقدار 1
def push(stack, item): 
	stack.append(item) 
	print(item + " pushed to stack ") 
	
# دالة لحذف عنصر من المكدس، وإنقاص حجم المكدس بمقدار 1
def pop(stack): 
	if (isEmpty(stack)): 
		return str(-maxsize -1) #تعيد القيمة سالب ما لا نهاية
	
	return stack.pop() 

# اختبار الدوال السابقة
stack = createStack() 
push(stack, str(10)) 
push(stack, str(20)) 
push(stack, str(30)) 
print(pop(stack) + " popped from stack")

• جافا:

class Stack 
{ 
	static final int MAX = 1000; 
	int top; 
	int a[] = new int[MAX]; // تعيين الحد الأعلى للكدس
    
	boolean isEmpty() 
	{ 
		return (top < 0); 
	} 
	Stack() 
	{ 
		top = -1; 
	} 

	boolean push(int x) 
	{ 
		if (top >= (MAX-1)) 
		{ 
			System.out.println("Stack Overflow"); 
			return false; 
		} 
		else
		{ 
			a[++top] = x; 
			System.out.println(x + " pushed into stack"); 
			return true; 
		} 
	} 

	int pop() 
	{ 
		if (top < 0) 
		{ 
			System.out.println("Stack Underflow"); 
			return 0; 
		} 
		else
		{ 
			int x = a[top--]; 
			return x; 
		} 
	} 
} 

// اختبار الدوال السابقة
class Main 
{ 
	public static void main(String args[]) 
	{ 
		Stack s = new Stack(); 
		s.push(10); 
		s.push(20); 
		s.push(30); 
		System.out.println(s.pop() + " Popped from stack"); 
	} 
}

تعطي الشيفرات السابقة المخرجات التالية:

10 pushed into stack
20 pushed into stack
30 pushed into stack
30 popped from stack

محاسن هذه الطريقة: سهلة التطبيق، ولا تستهلك الكثير من الذاكرة نظرًا لعدم استخدام المؤشرات.

مساوئ هذه الطريقة: غير ديناميكية، ولا تنمو أو تتقلص حسب الحاجة في وقت التشغيل.

تنفيذ المكادس باستخدام القوائم المترابطة

تعرض الأمثلة التالية طرق إنشاء الأكداس باستخدام القوائم المترابطة وفي عدد من لغات البرمجة:

• C++‎:

#include <bits/stdc++.h> 
using namespace std; 

// إنشاء بنية لتمثيل المكدس
class StackNode 
{ 
	public: 
	int data; 
	StackNode* next; 
}; 

StackNode* newNode(int data) 
{ 
	StackNode* stackNode = new StackNode(); 
	stackNode->data = data; 
	stackNode->next = NULL; 
	return stackNode; 
} 

int isEmpty(StackNode *root) 
{ 
	return !root; 
} 

void push(StackNode** root, int data) 
{ 
	StackNode* stackNode = newNode(data); 
	stackNode->next = *root; 
	*root = stackNode; 
	cout<<data<<" pushed to stack\n"; 
} 

int pop(StackNode** root) 
{ 
	if (isEmpty(*root)) 
		return INT_MIN; 
	StackNode* temp = *root; 
	*root = (*root)->next; 
	int popped = temp->data; 
	free(temp); 

	return popped; 
} 

int peek(StackNode* root) 
{ 
	if (isEmpty(root)) 
		return INT_MIN; 
	return root->data; 
} 

int main() 
{ 
	StackNode* root = NULL; 

	push(&root, 10); 
	push(&root, 20); 
	push(&root, 30); 

	cout<<pop(&root)<<" popped from stack\n"; 

	cout<<"Top element is "<<peek(root)<<endl; 

	return 0; 
}

• بايثون:

# صنف لتمثيل العقدة
class StackNode: 

	# دالة بانية لتهيئة العقدة
	def __init__(self, data): 
		self.data = data 
		self.next = None

class Stack: 
	
	# دالة بانية لتهيئة الجذر الخاص بالقائمة المترابطة 
	def __init__(self): 
		self.root = None

	def isEmpty(self): 
		return True if self.root is None else False

	def push(self, data): 
		newNode = StackNode(data) 
		newNode.next = self.root 
		self.root = newNode 
		print "%d pushed to stack" %(data) 
	
	def pop(self): 
		if (self.isEmpty()): 
			return float("-inf") 
		temp = self.root 
		self.root = self.root.next
		popped = temp.data 
		return popped 
	
	def peek(self): 
		if self.isEmpty(): 
			return float("-inf") 
		return self.root.data 

# اختبار الدوال السابقة
stack = Stack() 
stack.push(10)		 
stack.push(20) 
stack.push(30) 

print "%d popped from stack" %(stack.pop()) 
print "Top element is %d " %(stack.peek())

• جافا:

public class StackAsLinkedList { 

	StackNode root; 

	static class StackNode { 
		int data; 
		StackNode next; 

		StackNode(int data) { 
			this.data = data; 
		} 
	} 
	
	public boolean isEmpty() { 
		if (root == null) { 
			return true; 
		} else return false; 
	} 
	
	public void push(int data) { 
		StackNode newNode = new StackNode(data); 

		if (root == null) { 
			root = newNode; 
		} else { 
			StackNode temp = root; 
			root = newNode; 
			newNode.next = temp; 
		} 
		System.out.println(data + " pushed to stack"); 
	} 

	public int pop() { 
		int popped = Integer.MIN_VALUE; 
		if (root == null) { 
			System.out.println("Stack is Empty"); 
		} else { 
			popped = root.data; 
			root = root.next; 
		} 
		return popped; 
	} 

	public int peek() { 
		if (root == null) { 
			System.out.println("Stack is empty"); 
			return Integer.MIN_VALUE; 
		} else { 
			return root.data; 
		} 
		
	} 

	public static void main(String[] args) { 
		
		StackAsLinkedList sll = new StackAsLinkedList(); 

		sll.push(10); 
		sll.push(20); 
		sll.push(30); 

		System.out.println(sll.pop() + " popped from stack"); 
	
		System.out.println("Top element is " + sll.peek()); 


	} 

}

تعطي الشيفرات السابقة المخرجات التالية:

10 pushed to stack
20 pushed to stack
30 pushed to stack
30 popped from stack
Top element is 20

محاسن هذه الطريقة: يمكن لهذه الطريقة أن تنمو أو تتقلص حسب الحاجة في وقت التشغيل.

مساوئ هذه الطريقة: تحتاج إلى استخدام جزء أكبر من الذاكرة نظرًا لاستخدام المؤشرات.

إنشاء المكادس باستخدام الأرتال

يمكن استخدام الرتل Queue الذي يدعم عمليات مثل enqueue()‎ و dequeue()‎ لإنشاء المكدس Stack. وتتطلب هذه العملية استخدام طابورين (سنعطيهما الاسمين q1 و q2) ويمكن تنفيذها بطريقتين:

الطريقة الأولى: الاعتماد على عملية push

تحرص هذه العملية على أن يكون يضاف العنصر الجديد إلى مقدمة الرتل q1 وبهذا تزيل عملية pop العناصر من الرتل q1، ويستخدم الرتل q2 لوضع كل عنصر جديد في مقدمة الرتل q1.

يمكن تلخيص هذه الطريقة بالخطوات التالية:

1. العملية push(s, x)‎ حيث تمثل x العنصر المراد إضافته و s المكدس الذي سيضاف العنصر إليه.
   1. إضافة x إلى الرتل q2.
   2. إزالة كل العناصر من الرتل q1 واحدًا تلو الآخر وإضافتها إلى الرتل q2.
   3. تبديل أسماء الرتلين q1 و q2، والهدف من ذلك هو تجنب تحريك جميع العناصر من الرتل q2 إلى q1.
2. العملية pop(s)‎:
   1. إزالة العنصر من q1 وإعادته.

تعرض الأمثلة التالية طرق إنشاء المكادس باستخدام الأرتال وفي عدد من لغات البرمجة:

• C++‎:

#include<bits/stdc++.h> 

using namespace std; 

class Stack 
{ 
	// رتلان داخليان 
	queue<int> q1, q2; 
	
	// لمتابعة العدد الحالي للعناصر 
	 curr_size; 

	public: 
	Stack() 
	{ 
		curr_size = 0; 
	} 

	void push(int x) 
	{ 
		curr_size++; 

		// إضافة x إلى الرتل الثاني 
		q2.push(x); 

		// إضافة العناصر الباقية إلى الرتلين
		while (!q1.empty()) 
		{ 
			q2.push(q1.front()); 
			q1.pop(); 
		} 

		// تبديل أسماء الرتلين
		queue<int> q = q1; 
		q1 = q2; 
		q2 = q; 
	} 

	void pop(){ 

		// إن لم يكن هناك أي عنصر في الرتل الأول 
		if (q1.empty()) 
			return ; 
		q1.pop(); 
		curr_size--; 
	} 

	int top() 
	{ 
		if (q1.empty()) 
			return -1; 
		return q1.front(); 
	} 

	int size() 
	{ 
		return curr_size; 
	} 
}; 

// اختبار الدوال السابقة 
int main() 
{ 
	Stack s; 
	s.push(1); 
	s.push(2); 
	s.push(3); 

	cout << "current size: " << s.size() 
		<< endl; 
	cout << s.top() << endl; 
	s.pop(); 
	cout << s.top() << endl; 
	s.pop(); 
	cout << s.top() << endl; 

	cout << "current size: " << s.size() 
		<< endl; 
	return 0; 
}

• بايثون (ملاحظة: لتعمل هذه الشيفرة في الإصدار 2 من بايثون يجب استخدام الوحدة Queue عوضًا عن queue):

from queue import Queue

class Stack:

    def __init__(self):

        # رتلان داخليان
        self.q1 = Queue()
        self.q2 = Queue()

        # متابعة العدد الحالي من العناصر
        self.curr_size = 0

    def push(self, x):
        self.curr_size += 1

        # إضافة العنصر x إلى الرتل الثاني
        self.q2.put(x)

        # نقل جميع العناصر المتبقية من الرتل الأول إلى الثاني
        while (not self.q1.empty()):
            self.q2.put(self.q1.queue[0])
            self.q1.get()

        # تبديل اسمي الرتلين
        self.q = self.q1
        self.q1 = self.q2
        self.q2 = self.q

    def pop(self):

        # إن لم يكن هناك عناصر في الرتل الأول
        if (self.q1.empty()):
            return
        self.q1.get()
        self.curr_size -= 1

    def top(self):
        if (self.q1.empty()):
            return -1
        return self.q1.queue[0]

    def size(self):
        return self.curr_size

# اختبار الدوال السابقة
if __name__ == '__main__':
    s = Stack()
    s.push(1)
    s.push(2)
    s.push(3)

    print("current size: ", s.size())
    print(s.top())
    s.pop()
    print(s.top())
    s.pop()
    print(s.top())

    print("current size: ", s.size())

• Java:

import java.util.*; 

class GfG { 

static class Stack 
{ 
	// رتلان داخليان
	static Queue<Integer> q1 = new LinkedList<Integer>(); 
	static Queue<Integer> q2 = new LinkedList<Integer>(); 
	
	// الهدف من هذا المتغير هو متابعة العدد الحالي للعناصر
	static int curr_size; 

	Stack() 
	{ 
		curr_size = 0; 
	} 

	static void push(int x) 
	{ 
		curr_size++; 

		// إضافة العنصر x إلى الرتل الثاني 
		q2.add(x); 

		// نقل بقية العناصر من الرتل الأول إلى الثاني
		while (!q1.isEmpty()) 
		{ 
			q2.add(q1.peek()); 
			q1.remove(); 
		} 

		// تبديل أسماء الرتلين 
		Queue<Integer> q = q1; 
		q1 = q2; 
		q2 = q; 
	} 

	static void pop(){ 

		// إن لم يكن هناك عناصر في الرتل الأول 
		if (q1.isEmpty()) 
			return ; 
		q1.remove(); 
		curr_size--; 
	} 

	static int top() 
	{ 
		if (q1.isEmpty()) 
			return -1; 
		return q1.peek(); 
	} 

	static int size() 
	{ 
		return curr_size; 
	} 
}; 

// تجربة الدوال السابقة 
public static void main(String[] args) 
{ 
	Stack s = new Stack(); 
	s.push(1); 
	s.push(2); 
	s.push(3); 

	System.out.println("current size: " + s.size()); 
	System.out.println(s.top()); 
	s.pop(); 
	System.out.println(s.top()); 
	s.pop(); 
	System.out.println(s.top()); 

	System.out.println("current size: " + s.size()); 
} 
}

تعطي الشيفرات السابقة المخرجات التالية:

current size: 3
3
2
1
current size: 1

الطريقة الثانية: الاعتماد على عملية pop

يضاف العنصر الجديد دائمًا إلى الرتل q1 في عملية push، وفي العملية pop()‎ إن كان الرتل q2 فارغًا فإنّ جميع العناصر باستثناء العنصر الأخير ستُنقل إلى الرتل q2، ثم يزال العنصر الأخير من الرتل q1 ويعاد.

يمكن تلخيص هذه العملية بالخطوات التالية:

1. العملية push(s, x)‎:
   1. إضافة x إلى الرتل q1 (على فرض أنّ حجم الرتل q1 غير محدد).
2. العملية pop(s)‎:
   1. إزالة العناصر واحدًا تلو الآخر باستثناء العنصر الأخير من الرتل q1 وإضافتها غلى الرتل q2.
   2. إزالة العنصر الأخير من الرتل q1 وتخزينه.
   3. تبديل اسمي الرتلين q1 و q2، والهدف من ذلك هو تجنب إجراء عملية نقل جميع العناصر من الرتل q2 إلى q1.
   4. إعادة العنصر المخزن في الخطوة الثانية.

تعرض الأمثلة التالية طرق إنشاء المكادس باستخدام الأرتال وفي عدد من لغات البرمجة:

• C++‎:

#include<bits/stdc++.h> 
using namespace std; 

class Stack 
{ 
	queue<int> q1, q2; 
	int curr_size; 

	public: 
	Stack() 
	{ 
		curr_size = 0; 
	} 

	void pop() 
	{ 
		if (q1.empty()) 
			return; 
		// ترك عنصر واحد في الرتل الأول ونقل العناصر الباقية إلى الرتل الثاني
		while (q1.size() != 1) 
		{ 
			q2.push(q1.front()); 
			q1.pop(); 
		} 
		
        // حذف العنصر المتبقي من الرتل الأول
		q1.pop(); 
		curr_size--; 

		// تبديل اسمي الرتلين
		queue<int> q = q1; 
		q1 = q2; 
		q2 = q; 
	} 

	void push(int x) 
	{ 
		q1.push(x); 
		curr_size++; 
	} 

	int top() 
	{ 
		if (q1.empty()) 
			return -1; 

		while( q1.size() != 1 ) 
		{ 
		q2.push(q1.front()); 
		q1.pop(); 
		} 
		
		// العنصر المضاف الأخير 
		int temp = q1.front(); 
		
		// إفراغ الرتل الإضافي بعد إجراء آخر عملية
        q1.pop(); 
	
		// إضافة آخر عنصر إلى الرتل الثاني 
		q2.push(temp); 

		// تبديل اسمي الرتلين 
		queue<int> q = q1; 
		q1 = q2; 
		q2 = q; 
		return temp; 
	} 

	int size() 
	{ 
		return curr_size; 
	} 
}; 

// تجربة التوابع السابقة
int main() 
{ 
	Stack s; 
	s.push(1); 
	s.push(2); 
	s.push(3); 
	s.push(4); 

	cout << "current size: " << s.size() 
		<< endl; 
	cout << s.top() << endl; 
	s.pop(); 
	cout << s.top() << endl; 
	s.pop(); 
	cout << s.top() << endl; 
	cout << "current size: " << s.size() 
		<< endl; 
	return 0; 
}

تعطي الشيفرة السابقة المخرجات التالية:

current size: 4
4
3
2
current size: 2

قلب عناصر المكدس باستخدام دالة تعاودية

يمكن قلب عناصر المكدس باستخدام دالة تعاودية دون الحاجة إلى استخدام الحلقات التكرارية مثل while و for وغيرها، ويمكن الاستعانة بالدوال isEmpty(S)‎ و push(S)‎ و pop(S)‎ وذلك بتنفيذها على المكدس S.

تتلخص هذه الطريقة بالاحتفاظ بجميع القيم في مكدس استدعاء الدالة Function Call Stack إلى حين الحصول على مكدس فارغ، وعندها نبدأ بإدراج العناصر واحدًا تلو الآخر في أسفل المكدس.

لنفترض أن لدينا المكدس التالي:

    1  <-- top
    2
    3
    4

ندرج العنصر 4 في أسفل المكدس أولًا.

    4 <-- top

ثم ندرج العنصر 3 في أسفل المكدس.

    4 <-- top    
    3

ثم ندرج العنصر 2 في أسفل المكدس.

    4 <-- top    
    3 
    2

ثم ندرج العنصر 1 في أسفل المكدس.

    4 <-- top    
    3 
    2
    1

لذا سنحتاج إلى دالة تدرج العناصر في أسفل المكدس كما هو موضح في أعلاه.

الدالة insertAtBottom()‎: تحذف الدالة جميع العناصر الموجودة في المكدس وتخزّنها في مكدس استدعاء الدالة باستخدام التعاود recursion، وعندما يصبح المكدس فارغًا، تدفع الدالة العناصر المخزّنة في مكدس الاستدعاء.

الدالة reverse()‎: تستخدم هذه الدالةُ الدالةَ insertAtBottom()‎ بصورة رئيسية لحذف جميع العناصر واحدًا تلو الآخر وإضافة العناصر المحذوفة إلى أسفل المكدس.

• C++

#include<bits/stdc++.h> 
using namespace std; 

// using std::stack for 
// stack implementation 
stack<char> st; 

// تهيئة سلسلة نصية لتخزين النتائج الخاصة بالمكدس المعكوس
string ns; 

// الدالة التالية دالة تعاودية تدرج عنصرًا في أسفل المكدس.

char insert_at_bottom(char x) 
{ 

	if(st.size() == 0) 
	st.push(x); 

	else
	{ 
		// تحفظ جميع العناصر في مكدس استدعاء الدالة
        // إلى حين الوصول إلى نهاية المكدس
        // وعندما يصبح المكدس فارغًا
        // تصبح قيمة
        // st.size()
        // مساوية للصفر، وتنفذ العبارة الشرطية أعلاه
        // ويُدرج العنصر في أسفل المكدس
			
		char a = st.top(); 
		st.pop(); 
		insert_at_bottom(x); 

		// تدفع جميع العناصر المخزنة في
        // مكدس استدعاء الدالة
        // بعد إدراج العنصر في أسفل المكدس
        st.push(a); 
	} 
} 

// الدالة التالية تعكس عناصر المكدس
// باستخدام الدالة
// insert_at_bottom() 
char reverse() 
{ 
	if(st.size()>0) 
	{ 
		
		// تحفظ جميع العناصر في مكدس استدعاء الدالة
        // إلى حين الوصول إلى نهاية المكدس

		char x = st.top(); 
		st.pop(); 
		reverse(); 
		
        // إدراج جميع العناصر المخزنة في
        // مكدس استدعاء الدالة
        // واحدًا تلو الآخر من الأسفل إلى الأعلى
        // ويدرج كل عنصر في أسفل المكدس
		
        insert_at_bottom(x); 
	} 
} 

// اختبار الدوال السابقة
int main() 
{ 
	
    // إضافة عناصر إلى المكدس
	st.push('1'); 
	st.push('2'); 
	st.push('3'); 
	st.push('4'); 
	
	cout<<"Original Stack"<<endl; 
	
	// طباعة عناصر المكدس الأصلي
    cout<<"1"<<" "<<"2"<<" "
		<<"3"<<" "<<"4"
		<<endl; 
	
	// استدعاء الدالة التي تعكس المكدس
    reverse(); 
	cout<<"Reversed Stack"
		<<endl; 
	
	// تخزين قيم المكدس المعكوس
    // في سلسلة نصية لعرضها
    while(!st.empty()) 
	{ 
		char p=st.top(); 
		st.pop(); 
		ns+=p; 
	} 
	
	// عرض المكدس المعكوس
    cout<<ns[3]<<" "<<ns[2]<<" "
		<<ns[1]<<" "<<ns[0]<<endl; 
	return 0; 
}

• بايثون

# هذه الدالة دالة تعاودية
# تدرج العناصر في أسفل المكدس
def insertAtBottom(stack, item): 
	if isEmpty(stack): 
		push(stack, item) 
	else: 
		temp = pop(stack) 
		insertAtBottom(stack, item) 
		push(stack, temp) 

# تعكس الدال التالية ترتيب العناصر
# في المكدس المعطى باستخدام الدالة
# insertAtBottom() 
def reverse(stack): 
	if not isEmpty(stack): 
		temp = pop(stack) 
		reverse(stack) 
		insertAtBottom(stack, temp) 

# اختبار الدوال السابقة

# تنشئ هذه الدالة مكدسًا.
# وتهيئه ليكون بالحجم 0

def createStack(): 
	stack = [] 
	return stack 

# تتحق الدالة مما إذا كان المكدس فارغًا أو لا

def isEmpty( stack ): 
	return len(stack) == 0

# تدرج الدالة عنصرًا في المكدس
def push( stack, item ): 
	stack.append( item ) 

# تحذف الدالة عنصرًا من المكدس

def pop( stack ): 

	# إن كان المكدس فارغًا نطلق خطأً
    if(isEmpty( stack )): 
		print("Stack Underflow ") 
		exit(1) 

	return stack.pop() 

# دالة لطباعة عناصر المكدس
def prints(stack): 
	for i in range(len(stack)-1, -1, -1): 
		print(stack[i], end = ' ') 
	print() 

# اختبار الدوال السابقة

stack = createStack() 
push( stack, str(4) ) 
push( stack, str(3) ) 
push( stack, str(2) ) 
push( stack, str(1) ) 
print("Original Stack ") 
prints(stack) 

reverse(stack) 

print("Reversed Stack ") 
prints(stack)

• جافا

import java.util.Stack; 

class Test { 
	
	// Stack استخدام الصنف
    // لتهيئة المكدس
    static Stack<Character> st = new Stack<>(); 
	
	// الدالة التالية دالة تعاودية تدرج عنصرًا في أسفل المكدس.
	static void insert_at_bottom(char x) 
	{ 

		if(st.isEmpty()) 
			st.push(x); 

		else
		{ 
			
			// تحفظ جميع العناصر في مكدس استدعاء الدالة
	        // إلى حين الوصول إلى نهاية المكدس
	        // وعندما يصبح المكدس فارغًا
	        // تصبح قيمة
	        // st.size()
	        // مساوية للصفر، وتنفذ العبارة الشرطية أعلاه
	        // ويُدرج العنصر في أسفل المكدس

			char a = st.peek(); 
			st.pop(); 
			insert_at_bottom(x); 

            // تدفع جميع العناصر المخزنة في
        	// مكدس استدعاء الدالة
        	// بعد إدراج العنصر في أسفل المكدس

			st.push(a); 
		} 
	} 
	
	// الدالة التالية تعكس عناصر المكدس
	// باستخدام الدالة
	// insert_at_bottom() 
	static void reverse() 
	{ 
		if(st.size() > 0) 
		{ 
			
            // تحفظ جميع العناصر في مكدس استدعاء الدالة
            // إلى حين الوصول إلى نهاية المكدس

			char x = st.peek(); 
			st.pop(); 
			reverse(); 
			
	        // إدراج جميع العناصر المخزنة في
	        // مكدس استدعاء الدالة
	        // واحدًا تلو الآخر من الأسفل إلى الأعلى
	        // ويدرج كل عنصر في أسفل المكدس
		
			insert_at_bottom(x); 
		} 
	} 
	
	// اختبار الدوال السابقة
	public static void main(String[] args) 
	{ 
		
		// إضافة عناصر إلى المكدس
		st.push('1'); 
		st.push('2'); 
		st.push('3'); 
		st.push('4'); 
		
		System.out.println("Original Stack"); 
		
		System.out.println(st); 
		
		// تعكس هذه الدالة ترتيب العناصر في المكدس
		reverse(); 
		
		System.out.println("Reversed Stack"); 
		
		System.out.println(st); 
	} 
}

تعطي الشيفرة السابقة المعطيات التالية:

Original Stack 
 1  2  3  4 
 Reversed Stack 
 4  3  2  1

ترتيب عناصر المكدس باستخدام الدوال التعاودية

يمكن ترتيب عناصر المكدس باستخدام الدوال التعاودية ودون استخدام الحلقات التكرارية مثل while و for، ويمكن الاستعانة بالدوال التالية:

• is_empty(S)‎: تختبر الدالة ما إذا كان المكدس فارغًا أو لا.
• push(S)‎: تضيف الدالة عنصرًا جديدًا إلى المكدس.
• pop(S)‎: تحذف الدالة العنصر العلوي من المكدس.
• top(S)‎: تعيد الدالة قيمة العنصر العلوي في المكدس. لاحظ أنّ هذه الدالة لا تحذف العناصر من المكدس.

مثال:

Input:  -3  <--- Top
        14 
        18 
        -5 
        30 

Output: 30  <--- Top
        18 
        14 
        -3 
        -5

إن الطريقة المتّبعة لترتيب عناصر المكدس مشابهة إلى حدٍّ كبير للطريقة المتبعة في عكس ترتيب العناصر، إذ تتلخص الطريقة في تخزين جميع القيم في مكدس استدعاء الدالة إلى أن يصبح المكدس فارغًا، وعندئذٍ نُدرج جميع القيم المخزّنة واحدًا تلو الآخر وبالترتيب.

الخوارزمية المتبعة

يمكن استخدام الخوارزمية التالية لترتيب العناصر في المكدس:

sortStack(stack S)
    if stack is not empty:
        temp = pop(S);  
        sortStack(S); 
        sortedInsert(S, temp);

تعرض الخوارزمية التالية طريقة إدراج العنصر في المكدس وبالترتيب:

sortedInsert(Stack S, element)
    if stack is empty OR element > top element
        push(S, elem)
    else
        temp = pop(S)
        sortedInsert(S, element)
        push(S, temp)

مثال توضيحي

لنفترض أنّ لدينا المكدس التالي:

-3    <-- top of the stack
14
18
-5
30

الخطوة الأولى هي حذف جميع العناصر من المكدس وتخزينها في متغير مؤقت temp، وبعد حذف جميع العناصر سيبدو إطار مكدس الدالة function's stack frame بالشكل التالي:

temp = -3    --> stack frame #1
temp = 14    --> stack frame #2
temp = 18    --> stack frame #3
temp = -5    --> stack frame #4
temp = 30       --> stack frame #5

تستدعى الدالة insert_in_sorted_order()‎ بعد أن أصبح المكدس فارغًا وذلك لإدراج القيمة 30 (من إطار المكدس رقم 5) في أسفل المكدس، وبهذا يصبح المكدس:

30    <-- top of the stack

تلتقط الدالة العنصر التالي وهو ‎-5 (من إطار المكدس رقم 4)، ولما كان ‎-5 < 30 فإنّ العنصر ‎-5 سيُدرج في أسفل المكدس، وبهذا يصبح المكدس:

30    <-- top of the stack
-5

تلتقط الدالة العنصر التالي وهو 18 (من إطار المكدس رقم 3) ولما كان ‎18 < 30‎ فإنّ العنصر 18 سيُدرج تحت العنصر 30، وبهذا يصبح المكدس:

30    <-- top of the stack
18    
-5

تلتقط الدالة العنصر التالي وهو 14 (من إطار المكدس رقم 2) ولما كان ‎14 < 30‎ و ‎14 < 18 فإنّ العنصر 14 سيُدرج تحت العنصر 18، وبهذا يصبح المكدس:

30    <-- top of the stack
18
14    
-5

تلتقط الدالة العنصر التالي وهو ‎-3 (من إطار المكدس رقم 1) ولما كان ‎-3 < 30‎ و ‎-3 < 18 و ‎-3 < 14 فإنّ العنصر ‎-3 سيُدرج تحت العنصر 14، وبهذا يصبح المكدس:

30    <-- top of the stack
18
14
-3    
-5

أمثلة برمجية

تعرض الأمثلة التالية طريقة ترتيب عناصر المكدس في عدد من لغات البرمجة:

• C++‎

#include <stdio.h> 
#include <stdlib.h> 

// استخدمت القوائم المترابطة لإنشاء المكدس
struct stack 
{ 
	int data; 
	struct stack *next; 
}; 

// دالة مساعدة لتهيئة المكدس 
void initStack(struct stack **s) 
{ 
	*s = NULL; 
} 

// دالة مساعدة للتحقق من كون المكدس فارغًا أو لا
int isEmpty(struct stack *s) 
{ 
	if (s == NULL) 
		return 1; 
	return 0; 
} 

// دالة مساعدة لإدراج العناصر في المكدس
void push(struct stack **s, int x) 
{ 
	struct stack *p = (struct stack *)malloc(sizeof(*p)); 

	if (p == NULL) 
	{ 
		fprintf(stderr, "Memory allocation failed.\n"); 
		return; 
	} 

	p->data = x; 
	p->next = *s; 
	*s = p; 
} 

// دالة مساعدة لحذف العناصر من المكدس
int pop(struct stack **s) 
{ 
	int x; 
	struct stack *temp; 

	x = (*s)->data; 
	temp = *s; 
	(*s) = (*s)->next; 
	free(temp); 

	return x; 
} 

// دالة للبحث عن العنصر العلوي 
int top(struct stack *s) 
{ 
	return (s->data); 
} 

// دالة تعاودية لإدراج العنصر المعطى في المكدس حسب الترتيب

void sortedInsert(struct stack **s, int x) 
{ 
	// إما أن يكون المكدس فارغًا أو يكون العنصر المضاف
    // أكبر من العنصر العلوي، أي أكبر من جميع العناصر الموجودة
    
	if (isEmpty(*s) || x > top(*s)) 
	{ 
		push(s, x); 
		return; 
	} 

	// إن كان العنصر العلوي هو الأكبر فإنّ الدالة تحذفه وتستدعي نفسها مرة أخرى
    int temp = pop(s); 
	sortedInsert(s, x); 

	// إرجاع العنصر العلوي المحذوف سابقًا
    push(s, temp); 
} 

// دالة لترتيب عناصر المكدس
void sortStack(struct stack **s) 
{ 
	// إن لم يكن المكدس فارغًا
	if (!isEmpty(*s)) 
	{ 
		// احذف العنصر العلوي
		int x = pop(s); 

		// رتّب العناصر الباقية
		sortStack(s); 

		// أرجع العنصر العلوي مرة أخرى إلى قمة المكدس
		sortedInsert(s, x); 
	} 
} 

// دالة مساعدة لطباعة محتويات المكدس 
void printStack(struct stack *s) 
{ 
	while (s) 
	{ 
		printf("%d ", s->data); 
		s = s->next; 
	} 
	printf("\n"); 
} 

// اختبار الدوال السابقة
int main(void) 
{ 
	struct stack *top; 

	initStack(&top); 
	push(&top, 30); 
	push(&top, -5); 
	push(&top, 18); 
	push(&top, 14); 
	push(&top, -3); 

	printf("Stack elements before sorting:\n"); 
	printStack(top); 

	sortStack(&top); 
	printf("\n\n"); 

	printf("Stack elements after sorting:\n"); 
	printStack(top); 

	return 0; 
}

• جافا

// تستخدم الشيفرة صنف
// Stack
// معرّف مسبقًا لإجراء العمليات الخاصة بالمكدس

import java.util.ListIterator; 
import java.util.Stack; 

class Test 
{ 
	// طريقة تعاودية لإدراج عنصر في مكدس حسب الترتيب
    static void sortedInsert(Stack<Integer> s, int x) 
	{ 
		// إما أن يكون المكدس فارغًا أو يكون العنصر المضاف
    	// أكبر من العنصر العلوي، أي أكبر من جميع العناصر الموجودة
    
		if (s.isEmpty() || x > s.peek()) 
		{ 
			s.push(x); 
			return; 
		} 
	
		// إن كان العنصر العلوي هو الأكبر فإنّ الدالة ستحذفه وتستدعي نفسها مرة أخرى
		int temp = s.pop(); 
		sortedInsert(s, x); 
	
		// إرجاع العنصر العلوي المحذوف سابقًا
		s.push(temp); 
	} 
	
	// تابع لترتيب عناصر المكدس
	static void sortStack(Stack<Integer> s) 
	{ 
		// إن لم يكن المكدس فارغًا
		if (!s.isEmpty()) 
		{ 
			// احذف العنصر العلوي
			int x = s.pop(); 
	
			// رتّب بقية عناصر المكدس
			sortStack(s); 
	
			// أرجع العنصر العلوي إلى المكدس
			sortedInsert(s, x); 
		} 
	} 
	
	// دالة مساعدة لطباعة محتويات المكدس
	static void printStack(Stack<Integer> s) 
	{ 
	ListIterator<Integer> lt = s.listIterator(); 
		
	// الانتقال إلى العنصر التالي 
	while(lt.hasNext()) 
		lt.next(); 
		
	// طباعة العناصر من الأعلى إلى الأسفل
	while(lt.hasPrevious()) 
		System.out.print(lt.previous()+" "); 
	} 
	
	// اختبار الدوال السابقة 
	public static void main(String[] args) 
	{ 
		Stack<Integer> s = new Stack<>(); 
		s.push(30); 
		s.push(-5); 
		s.push(18); 
		s.push(14); 
		s.push(-3); 
	
		System.out.println("Stack elements before sorting: "); 
		printStack(s); 
	
		sortStack(s); 
	
		System.out.println(" \n\nStack elements after sorting:"); 
		printStack(s); 
	
	} 
}

ترتيب عناصر المكدس باستخدام مكدس آخر

يمكن ترتيب عناصر مكدس معين باستخدام مكدس آخر مؤقت، ويمكن أداء ذلك باتباع الخوارزمية التالية:

1. إنشاء مكدس مؤقت (tmpStack مثلًا).
2. ما دام المكدس الأصلي غير فارغ فيجب القيام بما يلي:
   1. سحب عنصر من المكدس الأصلي وتسميته temp.
   2. ما دام المكدس المؤقت غير فارغ وقيمة العنصر العلوي في المكدس المؤقت أكبر من قيمة temp اسحب عنصرًا من المكدس المؤقت وادفعه إلى المكدس الأصلي.
   3. ادفع العنصر temp إلى المكدس المؤقت.
3. ستكون الأرقام المرتبة في المكدس المؤقت tmpStack.

يمكن تمثيل هذه الخوارزمية بالخطوات المبسطة التالية:

المكدس الأصلي: ‎[34, 3, 31, 98, 92, 23]‎

العنصر الماخوذ: 23

المكدس الأصلي: ‎[34, 3, 31, 98, 92]‎

المكدس المؤقت: [23]

العنصر الماخوذ: 92

المكدس الأصلي: ‎[34, 3, 31, 98]‎

المكدس المؤقت: ‎[23, 92]‎

العنصر الماخوذ: 98

المكدس الأصلي: ‎[34, 3, 31]‎

المكدس المؤقت: ‎[23, 92, 98]‎

العنصر الماخوذ: 31

المكدس الأصلي: ‎[34, 3, 98, 92]‎

المكدس المؤقت: ‎[23, 31]‎

العنصر الماخوذ: 92

المكدس الأصلي: ‎[34, 3, 98]‎

المكدس المؤقت: ‎[23, 31, 92]‎

العنصر الماخوذ: 98

المكدس الأصلي: ‎[34, 3]‎

المكدس المؤقت: ‎[23, 31, 92, 98]‎

العنصر الماخوذ: 3

المكدس الأصلي: ‎[34, 98, 92, 31, 23]‎

المكدس المؤقت: [3]

العنصر الماخوذ: 23

المكدس الأصلي: ‎[34, 98, 92, 31]‎

المكدس المؤقت: ‎[3, 23]‎

العنصر الماخوذ: 31

المكدس الأصلي: ‎[34, 98, 92]‎

المكدس المؤقت: ‎[3, 23, 31]‎

العنصر الماخوذ: 92

المكدس الأصلي: ‎[34, 98]‎

المكدس المؤقت: ‎[3, 23, 31, 92]‎

العنصر الماخوذ: 98

المكدس الأصلي: [34]

المكدس المؤقت: ‎[3, 23, 31, 92, 98]‎

العنصر الماخوذ: 34

المكدس الأصلي: ‎[98, 92]‎

المكدس المؤقت: [3, 23, 31, 34]

العنصر الماخوذ: 92

المكدس الأصلي: [98]

المكدس المؤقت: ‎[3, 23, 31, 34, 92]‎

العنصر الماخوذ: 98

المكدس الأصلي: []

المكدس المؤقت: ‎[3, 23, 31, 34, 92, 98]‎

القائمة المرتبة النهائية: ‎[3, 23, 31, 34, 92, 98]‎

أمثلة برمجية

تعرض الأمثلة التالية طريقة ترتيب عناصر مكدس باستخدام مكدس آخر مؤقت وفي عدد من لغات البرمجة:

• C++‎

#include <bits/stdc++.h> 
using namespace std; 

// تعيد هذه الدالة المكدس المرتب
stack<int> sortStack(stack<int> &input) 
{ 
	stack<int> tmpStack; 

	while (!input.empty()) 
	{ 
		// إخراج العنصر الأول
		int tmp = input.top(); 
		input.pop(); 

        // ما دام المكدس المؤقت غير فارغٍ
        // والعنصر العلوي في المكدس أكبر من العنصر المؤقت
		while (!tmpStack.empty() && tmpStack.top() > tmp) 
		{ 
			// احذف عنصرًا من المكدس المؤقت وأضفه
            // إلى المكدس الأصلي
            input.push(tmpStack.top()); 
			tmpStack.pop(); 
		} 

		// أدرج العنصر المؤقت في المكدس المؤقت
		tmpStack.push(tmp); 
	} 

	return tmpStack; 
} 

int main() 
{ 
	stack<int> input; 
	input.push(34); 
	input.push(3); 
	input.push(31); 
	input.push(98); 
	input.push(92); 
	input.push(23); 

	// هذا هو المكدس المؤقت
	stack<int> tmpStack = sortStack(input); 
	cout << "Sorted numbers are:\n"; 

	while (!tmpStack.empty()) 
	{ 
		cout << tmpStack.top()<< " "; 
		tmpStack.pop(); 
	} 
}

• بايثون

# تعيد هذه الدالة المكدس المرتب
def sortStack ( stack ): 
	tmpStack = createStack() 
	while(isEmpty(stack) == False): 
		
		# احذف العنصر الأول 
		tmp = top(stack) 
		pop(stack) 

		# ما دام المكدس المؤقت غير فارغٍ
        # والعنصر العلوي في المكدس أكبر من العنصر المؤقت
	
		while(isEmpty(tmpStack) == False and
			int(top(tmpStack)) > int(tmp)): 
			
			# احذف عنصرًا من المكدس المؤقت وأضفه
            # إلى المكدس الأصلي

			push(stack,top(tmpStack)) 
			pop(tmpStack) 

		# أدرج العنصر المؤقت في المكدس المؤقت
		push(tmpStack,tmp) 
	
	return tmpStack 

# تنشئ هذه الدالة مكدسًا.
# وتهيئه ليكون بالحجم 0
def createStack(): 
	stack = [] 
	return stack 

# تتحق الدالة مما إذا كان المكدس فارغًا أو لا
def isEmpty( stack ): 
	return len(stack) == 0

# تدرج الدالة عنصرًا في المكدس
def push( stack, item ): 
	stack.append( item ) 

# تعيد الدالة العنصر العلوي في المكدس
def top( stack ): 
	p = len(stack) 
	return stack[p-1] 

# تحذف الدالة عنصرًا من المكدس

def pop( stack ): 

    # إن كان المكدس فارغًا نطلق خطأً

	if(isEmpty( stack )): 
		print("Stack Underflow ") 
		exit(1) 

	return stack.pop() 

# دالة لطباعة عناصر المكدس
def prints(stack): 
	for i in range(len(stack)-1, -1, -1): 
		print(stack[i], end = ' ') 
	print() 

# اختبار الدوال السابقة
stack = createStack() 
push( stack, str(34) ) 
push( stack, str(3) ) 
push( stack, str(31) ) 
push( stack, str(98) ) 
push( stack, str(92) ) 
push( stack, str(23) ) 

print("Sorted numbers are: ") 
sortedst = sortStack ( stack ) 
prints(sortedst)

• جافا

import java.util.*; 

class SortStack 
{ 
	// تعيد هذه الدالة المكدس المرتب
    public static Stack<Integer> sortstack(Stack<Integer> 
											input) 
	{ 
		Stack<Integer> tmpStack = new Stack<Integer>(); 
		while(!input.isEmpty()) 
		{ 
			// تحذف الدالة العنصر الأول 
			int tmp = input.pop(); 
		
            // ما دام المكدس المؤقت غير فارغٍ
            // والعنصر العلوي في المكدس أكبر من العنصر المؤقت

			while(!tmpStack.isEmpty() && tmpStack.peek() 
												> tmp) 
			{ 
				// احذف عنصرًا من المكدس المؤقت وأضفه
     	       // إلى المكدس الأصلي

			input.push(tmpStack.pop()); 
			} 
			
			// أضف العنصر المؤقت إلى المكدس المؤقت 
			tmpStack.push(tmp); 
		} 
		return tmpStack; 
	} 
	
	// اختبار الدوال السابقة
	public static void main(String args[]) 
	{ 
		Stack<Integer> input = new Stack<Integer>(); 
		input.add(34); 
		input.add(3); 
		input.add(31); 
		input.add(98); 
		input.add(92); 
		input.add(23); 
	
		// هذا هو المكدس المؤقت 
		Stack<Integer> tmpStack=sortstack(input); 
		System.out.println("Sorted numbers are:"); 
	
		while (!tmpStack.empty()) 
		{ 
			System.out.print(tmpStack.pop()+" "); 
		} 
	} 
}

المصادر

• صفحة Stack Data Structure (Introduction and Program في توثيق بنى المعطيات في موقع GeekforGeeks.
• صفحة Implement Stack using Queues من توثيق بنى المعطيات في موقع GeeksforGeeks.
• صفحة Reverse a stack using recursion في توثيق بنى المعطيات في موقع GeeksforGeeks.
• صفحة Sort a stack using recursion في توثيق بنى المعطيات في موقع GeeksforGeeks.
• صفحة Sort a stack using a temporary stack في توثيق بنى المعطيات في موقع GeeksforGeeks.