الفرق بين المراجعتين لصفحة: «Algorithms/Topological Sorting»
أنشأ الصفحة ب'<noinclude>{{DISPLAYTITLE:الترتيب الطوبولوجي}}</noinclude> الترتيب الطوبولوجي Topological Sorting للرسوم البيانية الم...' |
لا ملخص تعديل |
||
| سطر 4: | سطر 4: | ||
= الترتيب الطوبولوجي وعملية البحث بالعمق أولًا = | = الترتيب الطوبولوجي وعملية البحث بالعمق أولًا = | ||
تطبع عملية البحث بالعمق أولًا قيمة الرأس ثم تستدعي الدالة المسؤولة عن البحث تعاوديًا على الرؤوس المجاورة لهذا الرأس، أما في الترتيب الطوبولوجي فإنّنا بحاجة إلى طباعة قيمة الرأس قبل طباعة قيم الرؤوس المجاورة. فعلى سبيل المثال، في الرسم البياني أعلاه، يجب طباعة الرأس <code>5</code> قبل الرأس <code>0</code>، ولكن بخلاف عملية البحث بالعمق أولًا، فإنّ الرأس <code>4</code> يجب أن يطبع قبل الرأس <code>0</code>؛ لذا فإنّ الترتيب الطوبولوجي مختلف عن عملية البحث بالعمق أولًا، فعلى سبيل المثال تكون نتيجة عملية البحث بالعمق أولًا للرسم البياني أعلاه هي "<code>5 2 3 1 0 4</code>" ولكنّه ليس ترتيبًا طوبولوجيًا. | تطبع عملية [[Algorithms/graphs#.D8.A7.D9.84.D8.A8.D8.AD.D8.AB .D8.A8.D8.A7.D9.84.D8.B9.D9.85.D9.82 .D8.A3.D9.88.D9.84.D9.8B.D8.A7 .D9.81.D9.8A .D8.A7.D9.84.D8.B1.D8.B3.D9.88.D9.85 .D8.A7.D9.84.D8.A8.D9.8A.D8.A7.D9.86.D9.8A.D8.A9|البحث بالعمق أولًا]] قيمة الرأس ثم تستدعي الدالة المسؤولة عن البحث تعاوديًا على الرؤوس المجاورة لهذا الرأس، أما في الترتيب الطوبولوجي فإنّنا بحاجة إلى طباعة قيمة الرأس قبل طباعة قيم الرؤوس المجاورة. | ||
[[ملف:topological1.png|بديل=رسم بياني موجه|مركز|رسم بياني موجه]] | |||
فعلى سبيل المثال، في الرسم البياني أعلاه، يجب طباعة الرأس <code>5</code> قبل الرأس <code>0</code>، ولكن بخلاف عملية البحث بالعمق أولًا، فإنّ الرأس <code>4</code> يجب أن يطبع قبل الرأس <code>0</code>؛ لذا فإنّ الترتيب الطوبولوجي مختلف عن عملية البحث بالعمق أولًا، فعلى سبيل المثال تكون نتيجة عملية البحث بالعمق أولًا للرسم البياني أعلاه هي "<code>5 2 3 1 0 4</code>" ولكنّه ليس ترتيبًا طوبولوجيًا. | |||
== خوارزمية إيجاد الترتيب الطوبولوجي == | == خوارزمية إيجاد الترتيب الطوبولوجي == | ||
يمكن تعديل عملية البحث بالعمق أولًا لإيجاد الترتيب الطوبولوجي لرسم بياني معيّن، إذ نبدأ من الرأس ونطبع قيمته في البداية ثم نستدعي الدالة تعاوديًا على الرؤوس المجاورة له، أما في الترتيب الطوبولوجي فنستخدم كدسًا stack مؤقتًا، ولا نطبع قيمة الرأس مباشرة، بل نستدعي الدالة المسؤولة عن إيجاد الترتيب الطوبولوجي تعاوديًا على جميع العناصر المجاورة للرأس، ثم ندفع بالرأس إلى الكدس، وفي النهاية نطبع محتويات الكدس. لاحظ أنّ الرأس يُدفع إلى الرأس فقط عندما تكون جميع الرؤوس المجاورة له (والرؤوس المجاورة لها وهكذا دواليك) موجودة فعلًا في الكدس. | يمكن تعديل عملية البحث بالعمق أولًا لإيجاد الترتيب الطوبولوجي لرسم بياني معيّن، إذ نبدأ من الرأس ونطبع قيمته في البداية ثم نستدعي الدالة تعاوديًا على الرؤوس المجاورة له، أما في الترتيب الطوبولوجي فنستخدم [[Algorithms/stacks|كدسًا stack]] مؤقتًا، ولا نطبع قيمة الرأس مباشرة، بل نستدعي الدالة المسؤولة عن إيجاد الترتيب الطوبولوجي تعاوديًا على جميع العناصر المجاورة للرأس، ثم ندفع بالرأس إلى الكدس، وفي النهاية نطبع محتويات الكدس. لاحظ أنّ الرأس يُدفع إلى الرأس فقط عندما تكون جميع الرؤوس المجاورة له (والرؤوس المجاورة لها وهكذا دواليك) موجودة فعلًا في الكدس. | ||
يجدر التنبيه إلى أنّ بالإمكان استخدام المتجه vector عوضًا عن المكدس، وفي هذه الحالة يجب طباعة العناصر بترتيب معكوس للحصول على الترتيب الطوبولوجي. | يجدر التنبيه إلى أنّ بالإمكان استخدام المتجه vector عوضًا عن المكدس، وفي هذه الحالة يجب طباعة العناصر بترتيب معكوس للحصول على الترتيب الطوبولوجي. | ||
== | == تنفيذ الخوارزمية == | ||
تعرض الأمثلة التالية طريقة تنفيذ خوارزمية إيجاد الترتيب الطوبولوجي في عدد من لغات البرمجة: | تعرض الأمثلة التالية طريقة تنفيذ خوارزمية إيجاد الترتيب الطوبولوجي في عدد من لغات البرمجة: | ||
| سطر 261: | سطر 264: | ||
== التعقيد الزمني == | == التعقيد الزمني == | ||
هذه الخوارزمية هي خوارزمية [[Algorithms/graphs#.D8.A7.D9.84.D8.A8.D8.AD.D8.AB .D8.A8.D8.A7.D9.84.D8.B9.D9.85.D9.82 .D8.A3.D9.88.D9.84.D9.8B.D8.A7 .D9.81.D9.8A .D8.A7.D9.84.D8.B1.D8.B3.D9.88.D9.85 .D8.A7.D9.84.D8.A8.D9.8A.D8.A7.D9.86.D9.8A.D8.A9|البحث بالعمق أولًا]] مع مكدس إضافي؛ لذا فإن التعقيد الزمني لهذه العملية مشابه للتعقيد الزمني لخوارزمية [[Algorithms/graphs#.D8.A7.D9.84.D8.A8.D8.AD.D8.AB .D8.A8.D8.A7.D9.84.D8.B9.D9.85.D9.82 .D8.A3.D9.88.D9.84.D9.8B.D8.A7 .D9.81.D9.8A .D8.A7.D9.84.D8.B1.D8.B3.D9.88.D9.85 .D8.A7.D9.84.D8.A8.D9.8A.D8.A7.D9.86.D9.8A.D8.A9|البحث بالعمق أولًا]]، ويبلغ <code>O(V+E)</code>. | |||
== التطبيقات == | == التطبيقات == | ||
يستخدم الترتيب الطوبولوجي بصورة رئيسية في | يستخدم الترتيب الطوبولوجي بصورة رئيسية في جدولة الأعمال من الاعتماديات المعطاة. ويمكن ملاحظة مثل هذا النوع من التطبيقات في علوم الحاسوب في عمليات جدولة التعليمات instruction scheduling، و ترتيب عملية معالجة خلية الصيغة formula cell evaluation عند إعادة حساب القيم الناتجة من صيغة معينة في الجداول الحسابية، وفي التصميم المنطقي Logic synthesis، وفي تحديد ترتيب مهام التصريف في ملفات makefiles، وفي سلسلة البيانات، وفي تحليل اعتماديات الرموز symbol dependencies في الرابطات linkers. | ||
== طباعة جميع الاحتمالات الممكنة لعملية الترتيب الطوبولوجي == | == طباعة جميع الاحتمالات الممكنة لعملية الترتيب الطوبولوجي == | ||
لنأخذ الرسم البياني التالي كمثال: | لنأخذ الرسم البياني التالي كمثال: | ||
[[ملف:topological1.png|بديل=رسم بياني موجه|مركز|رسم بياني موجه]] | |||
الاحتمالات الممكنة لعملية الترتيب الطوبولوجي المجراة على هذا الرسم البياني هي: | الاحتمالات الممكنة لعملية الترتيب الطوبولوجي المجراة على هذا الرسم البياني هي: | ||
| سطر 286: | سطر 290: | ||
5 4 2 3 0 1 | 5 4 2 3 0 1 | ||
5 4 2 3 1 0 </source> | 5 4 2 3 1 0 </source> | ||
عند التعامل مع الرسوم البيانية غير الدائرية والموجّهة يكون هناك احتمال لوجود رؤوس غير مرتبة ببعضها البعض؛ ولهذا السبب لا يمكن ترتيب هذه الرؤوس بطرق مختلفة. إن نتائج الترتيب الطوبولوجي المختلفة هذه مهمّة جدًّا في الكثير من الحالات، فعلى سبيل المثال إن توفّر وزن نسبي بين الرؤوس، والذي يعني | عند التعامل مع الرسوم البيانية غير الدائرية والموجّهة يكون هناك احتمال لوجود رؤوس غير مرتبة ببعضها البعض؛ ولهذا السبب لا يمكن ترتيب هذه الرؤوس بطرق مختلفة. إن نتائج الترتيب الطوبولوجي المختلفة هذه مهمّة جدًّا في الكثير من الحالات، فعلى سبيل المثال إن توفّر وزن نسبي بين الرؤوس، والذي يعني تقليل القيم وأننا بحاجة إلى الاعتناء بالترتيب النسبي إلى جانب الوزن النسبي، والذي يعني بدوره الحاجة إلى التحقق من جيع الاحتمالات الممكنة لعملية الترتيب الطوبولوجي. | ||
يمكن الحصول على جميع الاحتمالات الممكنة لعملية الترتيب الطوبولوجي بواسطة التعقب الخلفي backtracking، ويمكن تقسيم الخوارزمية المتّبعة إلى الخطوات التالية: | يمكن الحصول على جميع الاحتمالات الممكنة لعملية الترتيب الطوبولوجي بواسطة التعقب الخلفي backtracking، ويمكن تقسيم الخوارزمية المتّبعة إلى الخطوات التالية: | ||
| سطر 294: | سطر 298: | ||
# بعد انتهاء عمل الدالة نعيد تعيين قيم كل من الرؤوس المزورة والنتيجة وعدد الأضلاع المشيرة وذلك لحساب الاحتمالات الأخرى. | # بعد انتهاء عمل الدالة نعيد تعيين قيم كل من الرؤوس المزورة والنتيجة وعدد الأضلاع المشيرة وذلك لحساب الاحتمالات الأخرى. | ||
=== | === تنفيذ الخوارزمية === | ||
تعرض الأمثلة التالية طريقة تنفيذ هذه الخوارزمية في عدد من لغات البرمجة: | تعرض الأمثلة التالية طريقة تنفيذ هذه الخوارزمية في عدد من لغات البرمجة: | ||
| سطر 530: | سطر 534: | ||
} | } | ||
</source> | </source> | ||
== انظر أيضًا == | |||
* [[Algorithms/Kahn|خوارزمية كان للترتيب الطوبولوجي]] | |||
== مصادر == | == مصادر == | ||
مراجعة 12:35، 20 أكتوبر 2019
الترتيب الطوبولوجي Topological Sorting للرسوم البيانية الموجّهة غير الدائرية، هو ترتيب خطي للرؤوس يأتي فيه الرأس u قبل الرأس v في الترتيب لكل ضلع u-v موجّه. ولا يمكن إجراء الترتيب الطوبولوجي على الرسم البياني إلا إذا كان موجّهًا وغير دائري. على سبيل المثال، يكون الترتيب الطوبولوجي للرسم البياني أدناه هو "5 4 2 3 1 0"، ويمكن أن يكون هناك أكثر من ترتيب واحد لرسم البياني، إذ يمكن مثلًا أن يكون الترتيب الطوبولوجي للرسم البياني نفسه هو "4 5 2 3 1 0". يمتلك الرأس الأول في الترتيب الطوبولوجي الدرجة 0 دائمًا (أي أنّه رأس لا يشير إليه أي ضلع من أضلاع الرسم البياني).
الترتيب الطوبولوجي وعملية البحث بالعمق أولًا
تطبع عملية البحث بالعمق أولًا قيمة الرأس ثم تستدعي الدالة المسؤولة عن البحث تعاوديًا على الرؤوس المجاورة لهذا الرأس، أما في الترتيب الطوبولوجي فإنّنا بحاجة إلى طباعة قيمة الرأس قبل طباعة قيم الرؤوس المجاورة.
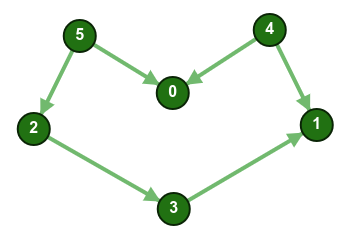
فعلى سبيل المثال، في الرسم البياني أعلاه، يجب طباعة الرأس 5 قبل الرأس 0، ولكن بخلاف عملية البحث بالعمق أولًا، فإنّ الرأس 4 يجب أن يطبع قبل الرأس 0؛ لذا فإنّ الترتيب الطوبولوجي مختلف عن عملية البحث بالعمق أولًا، فعلى سبيل المثال تكون نتيجة عملية البحث بالعمق أولًا للرسم البياني أعلاه هي "5 2 3 1 0 4" ولكنّه ليس ترتيبًا طوبولوجيًا.
خوارزمية إيجاد الترتيب الطوبولوجي
يمكن تعديل عملية البحث بالعمق أولًا لإيجاد الترتيب الطوبولوجي لرسم بياني معيّن، إذ نبدأ من الرأس ونطبع قيمته في البداية ثم نستدعي الدالة تعاوديًا على الرؤوس المجاورة له، أما في الترتيب الطوبولوجي فنستخدم كدسًا stack مؤقتًا، ولا نطبع قيمة الرأس مباشرة، بل نستدعي الدالة المسؤولة عن إيجاد الترتيب الطوبولوجي تعاوديًا على جميع العناصر المجاورة للرأس، ثم ندفع بالرأس إلى الكدس، وفي النهاية نطبع محتويات الكدس. لاحظ أنّ الرأس يُدفع إلى الرأس فقط عندما تكون جميع الرؤوس المجاورة له (والرؤوس المجاورة لها وهكذا دواليك) موجودة فعلًا في الكدس.
يجدر التنبيه إلى أنّ بالإمكان استخدام المتجه vector عوضًا عن المكدس، وفي هذه الحالة يجب طباعة العناصر بترتيب معكوس للحصول على الترتيب الطوبولوجي.
تنفيذ الخوارزمية
تعرض الأمثلة التالية طريقة تنفيذ خوارزمية إيجاد الترتيب الطوبولوجي في عدد من لغات البرمجة:
- C++:
#include<iostream>
#include <list>
#include <stack>
using namespace std;
// صنف يمثّل الرسم البياني
class Graph
{
int V; // عدد الرؤوس
// مؤشر إلى مصفوفة تحتوي على قائمة بقائمة المجاورة
list<int> *adj;
// الدالة المسؤولة عن تنفيذ خوارزمية الترتيب الطوبولوجي
void topologicalSortUtil(int v, bool visited[], stack<int> &Stack);
public:
Graph(int V); // بناء الكائن
// دالة لإضافة ضلع إلى الرسم البياني
void addEdge(int v, int w);
// طباعة الترتيب الطوبولوجي لرسم بياني كامل
void topologicalSort();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // إضافة الضلع المعطى إلى قائمة الأضلاع
}
// topolologicalsort دالة تعاودية تستخدمها الدالة
void Graph::topologicalSortUtil(int v, bool visited[],
stack<int> &Stack)
{
// تعليم العقدة الحالية على أنّها عقدة مزورة
visited[v] = true;
// تنفيذ الدالة تعاوديًا على جميع الرؤوس المجاورة لهذا الرأس
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
topologicalSortUtil(*i, visited, Stack);
// إضافة الرأس الحالي إلى الكدس الذي يخزّن النتيجة
Stack.push(v);
}
// الدالة التي تجري عملية الترتيب الطوبولوجي. تستخدم الدالة التعاودية
// topologicalSortUtil()
void Graph::topologicalSort()
{
stack<int> Stack;
// تعليم جميع الرؤوس على أنّها غير مزورة
bool *visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
// استدعاء الدالة التعاودية المساعدة لتخزين الترتيب الطوبولوجي
// لجميع الرؤوس واحدًا تلو الآخر
for (int i = 0; i < V; i++)
if (visited[i] == false)
topologicalSortUtil(i, visited, Stack);
// طباعة محتويات الكدس
while (Stack.empty() == false)
{
cout << Stack.top() << " ";
Stack.pop();
}
}
// اختبار الدوال السابقة
int main()
{
// إنشاء الرسم البياني أعلاه
Graph g(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
cout << "Following is a Topological Sort of the given graph \n";
g.topologicalSort();
return 0;
}
- بايثون:
from collections import defaultdict
# صنف لتمثيل الرسم البياني
class Graph:
def __init__(self,vertices):
self.graph = defaultdict(list) #dictionary containing adjacency List
self.V = vertices #No. of vertices
# دالة لإضافة ضلع إلى الرسم البياني
def addEdge(self,u,v):
self.graph[u].append(v)
# topologicalSort دالة تعاودية تستخدمها الدالة
def topologicalSortUtil(self,v,visited,stack):
# تعليم العقدة الحالية على أنّها مزورة
visited[v] = True
# استدعاء الدالة تعاوديًا على جميع الرؤوس المجاورة لهذا الرأس
for i in self.graph[v]:
if visited[i] == False:
self.topologicalSortUtil(i,visited,stack)
# إدراج الرأس الحالي إلى المكدس الذي يخزّن النتيجة
stack.insert(0,v)
# الدالة المسؤولة عن عملية الترتيب الطوبولوجي. تستخدم الدالة التعاودية
# topologicalSortUtil()
def topologicalSort(self):
# تعليم جميع الرؤوس على أنّها غير مزورة
visited = [False]*self.V
stack =[]
# استدعاء الدالة التعاودية المساعدة لتخزين نتيجة الترتيب الطوبولوجي
# لجميع الرؤوس واحدًا تلو الآخر
for i in range(self.V):
if visited[i] == False:
self.topologicalSortUtil(i,visited,stack)
# طباعة محتوى المكدس
print stack
g= Graph(6)
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
print "Following is a Topological Sort of the given graph"
g.topologicalSort()
- جافا:
import java.io.*;
import java.util.*;
// يستخدم هذا الصنف لتمثيل الرسم البياني الموجه باستخدام قائمة المجاورة
class Graph
{
private int V; // عدد الرؤوس
private LinkedList<Integer> adj[]; // قائمة المجاورة
// إنشاء الكائن
Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
// دالة لإضالة ضلع إلى الرسم البياني
void addEdge(int v,int w) { adj[v].add(w); }
// topologicalSort دالة تعاودية تستخدمها الدالة
void topologicalSortUtil(int v, boolean visited[],
Stack stack)
{
// تعليم العقدة الحالية على أنّها مزورة
visited[v] = true;
Integer i;
// تنفيذ الدالة تعاوديًا على جميع الرؤوس المجاورة لهذا الرأس
Iterator<Integer> it = adj[v].iterator();
while (it.hasNext())
{
i = it.next();
if (!visited[i])
topologicalSortUtil(i, visited, stack);
}
// إدراج الرأس الحالي في المكدس الذي يخزّن النتيجة
stack.push(new Integer(v));
}
// الدالة المسؤولة عن عملية الترتيب الطوبولوجي.
// تستخدم الدالة التعاودية
// topologicalSortUtil()
void topologicalSort()
{
Stack stack = new Stack();
// تعليم جميع الرؤوس على أنّها غير مزورة
boolean visited[] = new boolean[V];
for (int i = 0; i < V; i++)
visited[i] = false;
// استدعاء الدالة التعاودية المساعدة لتخزين نتيجة
// عملية الترتيب الطوبولوجي لجميع الرؤوس واحدًا تلو الآخر
for (int i = 0; i < V; i++)
if (visited[i] == false)
topologicalSortUtil(i, visited, stack);
// طباعة محتويات المكدس
while (stack.empty()==false)
System.out.print(stack.pop() + " ");
}
// اختبار التوابع السابقة
public static void main(String args[])
{
// إنشاء الرسم البياني في أعلاه
Graph g = new Graph(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
System.out.println("Following is a Topological " +
"sort of the given graph");
g.topologicalSort();
}
}
تعطي الشيفرات السابقة المخرجات التالية:
Following is a Topological Sort of the given graph
5 4 2 3 1 0
التعقيد الزمني
هذه الخوارزمية هي خوارزمية البحث بالعمق أولًا مع مكدس إضافي؛ لذا فإن التعقيد الزمني لهذه العملية مشابه للتعقيد الزمني لخوارزمية البحث بالعمق أولًا، ويبلغ O(V+E).
التطبيقات
يستخدم الترتيب الطوبولوجي بصورة رئيسية في جدولة الأعمال من الاعتماديات المعطاة. ويمكن ملاحظة مثل هذا النوع من التطبيقات في علوم الحاسوب في عمليات جدولة التعليمات instruction scheduling، و ترتيب عملية معالجة خلية الصيغة formula cell evaluation عند إعادة حساب القيم الناتجة من صيغة معينة في الجداول الحسابية، وفي التصميم المنطقي Logic synthesis، وفي تحديد ترتيب مهام التصريف في ملفات makefiles، وفي سلسلة البيانات، وفي تحليل اعتماديات الرموز symbol dependencies في الرابطات linkers.
طباعة جميع الاحتمالات الممكنة لعملية الترتيب الطوبولوجي
لنأخذ الرسم البياني التالي كمثال:

الاحتمالات الممكنة لعملية الترتيب الطوبولوجي المجراة على هذا الرسم البياني هي:
4 5 0 2 3 1
4 5 2 0 3 1
4 5 2 3 0 1
4 5 2 3 1 0
5 2 3 4 0 1
5 2 3 4 1 0
5 2 4 0 3 1
5 2 4 3 0 1
5 2 4 3 1 0
5 4 0 2 3 1
5 4 2 0 3 1
5 4 2 3 0 1
5 4 2 3 1 0
عند التعامل مع الرسوم البيانية غير الدائرية والموجّهة يكون هناك احتمال لوجود رؤوس غير مرتبة ببعضها البعض؛ ولهذا السبب لا يمكن ترتيب هذه الرؤوس بطرق مختلفة. إن نتائج الترتيب الطوبولوجي المختلفة هذه مهمّة جدًّا في الكثير من الحالات، فعلى سبيل المثال إن توفّر وزن نسبي بين الرؤوس، والذي يعني تقليل القيم وأننا بحاجة إلى الاعتناء بالترتيب النسبي إلى جانب الوزن النسبي، والذي يعني بدوره الحاجة إلى التحقق من جيع الاحتمالات الممكنة لعملية الترتيب الطوبولوجي.
يمكن الحصول على جميع الاحتمالات الممكنة لعملية الترتيب الطوبولوجي بواسطة التعقب الخلفي backtracking، ويمكن تقسيم الخوارزمية المتّبعة إلى الخطوات التالية:
- تهيئة جميع العقد لتكون غير مزورة.
- اختيار الرأس الذي يكون غير موزرٍ والذي لا يشير إليه أي ضلع من أضلاع الرسم البياني، وتخفيض عدد الأضلاع التي تشير إلى جميع هذه الرؤوس بمقدر 1 (وذلك نتيجة لحذف الأضلاع) ثم إضافة هذه الرأس إلى النتيجة واستدعاء الدالة التعاودية مرة أخرى وإجراء التعقب الخلفي.
- بعد انتهاء عمل الدالة نعيد تعيين قيم كل من الرؤوس المزورة والنتيجة وعدد الأضلاع المشيرة وذلك لحساب الاحتمالات الأخرى.
تنفيذ الخوارزمية
تعرض الأمثلة التالية طريقة تنفيذ هذه الخوارزمية في عدد من لغات البرمجة:
#include <bits/stdc++.h>
using namespace std;
class Graph
{
int V; // عدد الرؤوس
// مؤشر إلى مصفوفة تحتوي على قائمة المجاورة
list<int> *adj;
// متّجه لتخزين عدد الأضلاع المشيرة إلى عقدة معينة
vector<int> indegree;
// alltopologicalSort دالة تستخدمها الدالة
void alltopologicalSortUtil(vector<int>& res,
bool visited[]);
public:
Graph(int V); // إنشاء الكائن
// دالة لإضافة ضلع إلى الرسم البياني
void addEdge(int v, int w);
// طباعة جميع احتمالات الترتيب الطوبولوجي
void alltopologicalSort();
};
// إنشاء الرسم البياني
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
// تهيئة جميع الأضلع المشيرة إلى الرؤوس لتكون 0
for (int i = 0; i < V; i++)
indegree.push_back(0);
}
// دالة مساعدة لإضافة ضلع إلى الرسم البياني
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // إضافة الضلع المعطى إلى قائمة الأضلاع
// زيادة مقدار الإشارة الداخلية بمقدار 1
indegree[w]++;
}
// الدالة التعاودية الرئيسة المسؤولة عن طباعة
// جميع الاحتمالات الممكنة لعملية الترتيب الطوبولوجي
void Graph::alltopologicalSortUtil(vector<int>& res,
bool visited[])
{
// للإشارة إلى العثور على جميع التراتيب الطوبولوجية
bool flag = false;
for (int i = 0; i < V; i++)
{
// إن كانت درجة الدخول 0 وكان الرأس غير مزور بعد
// سنختار ذلك الرأس فقط
if (indegree[i] == 0 && !visited[i])
{
// تخفيض قيمة درجة الدخول للرؤوس المجاورة
list<int>:: iterator j;
for (j = adj[i].begin(); j != adj[i].end(); j++)
indegree[*j]--;
// تضمين الترتيب في مصفوفة النتيجة
res.push_back(i);
visited[i] = true;
alltopologicalSortUtil(res, visited);
// إعادة تعيين قيم كل من الرؤوس المزورة، والنتيجة
// ودرجة الدخول لأجل إجراء عملية التعقب الخلفي مرة أخرى
visited[i] = false;
res.erase(res.end() - 1);
for (j = adj[i].begin(); j != adj[i].end(); j++)
indegree[*j]++;
flag = true;
}
}
// نصل إلى هذه النطقة عندما تكون جميع العقد مزورة
// لذا نطبع الحلّ هنا
if (!flag)
{
for (int i = 0; i < res.size(); i++)
cout << res[i] << " ";
cout << endl;
}
}
// تؤدي هذه الدالة عملية الترتيب الطوبولوجي
// alltopologicalSortUtil() تستخدم الدالة التعاودية
void Graph::alltopologicalSort()
{
// تعليم جميع الرؤوس على أنّها مزورة
bool *visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
vector<int> res;
alltopologicalSortUtil(res, visited);
}
// اختبار الدوال السابقة
int main()
{
// إنشاء الرسم البياني أعلاه
Graph g(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
cout << "All Topological sorts\n";
g.alltopologicalSort();
return 0;
}
- جافا:
import java.util.*;
class Graph {
int V; // عدد الرؤوس
List<Integer> adjListArray[];
public Graph(int V) {
this.V = V;
@SuppressWarnings("unchecked")
List<Integer> adjListArray[] = new LinkedList[V];
this.adjListArray = adjListArray;
for (int i = 0; i < V; i++) {
adjListArray[i] = new LinkedList<>();
}
}
// دالة مساعدة لإضافة ضلع إلى الرسم البياني
public void addEdge(int src, int dest) {
this.adjListArray[src].add(dest);
}
// الدالة التعاودية الرئيسة المسؤولة عن إحصاء
// جميع الاحتمالات الممكنة لعملية الترتيب الطوبولوجي
private void allTopologicalSortsUtil(boolean[] visited,
int[] indegree, ArrayList<Integer> stack) {
// للإشارة إلى أنّه قد تم العثور على جميع الاحتمالات الممكنة
boolean flag = false;
for (int i = 0; i < this.V; i++) {
// إن كانت درجة الدخول 0 وكان الرأس غير مزور بعد
// سنختار ذلك الرأس فقط
if (!visited[i] && indegree[i] == 0) {
// إضافة الحاصل إلى النتيجة النهائية
visited[i] = true;
stack.add(i);
for (int adjacent : this.adjListArray[i]) {
indegree[adjacent]--;
}
allTopologicalSortsUtil(visited, indegree, stack);
// إعادة تعيين قيم كل من الرأس المزور، والحاصل، ودرجة الدخول
// لغرض إجراء عملية التعقب الخلفي
visited[i] = false;
stack.remove(stack.size() - 1);
for (int adjacent : this.adjListArray[i]) {
indegree[adjacent]++;
}
flag = true;
}
}
// نصل إلى هنا عندما تكون جميع الرؤوس مزورة
// لذا نطبع الحل هنا
if (!flag) {
stack.forEach(i -> System.out.print(i + " "));
System.out.println();
}
}
// الدالة التي تؤدي عملية الترتيب الطوبولوجي
// alltopologicalSortUtil() تستخدم الدالة
public void allTopologicalSorts() {
// تعليم جميع الرؤوس على أنّها غير مزورة
boolean[] visited = new boolean[this.V];
int[] indegree = new int[this.V];
for (int i = 0; i < this.V; i++) {
for (int var : this.adjListArray[i]) {
indegree[var]++;
}
}
ArrayList<Integer> stack = new ArrayList<>();
allTopologicalSortsUtil(visited, indegree, stack);
}
// اختبار الشيفرة السابقة
public static void main(String[] args) {
// إنشاء الرسم البياني أعلاه
Graph graph = new Graph(6);
graph.addEdge(5, 2);
graph.addEdge(5, 0);
graph.addEdge(4, 0);
graph.addEdge(4, 1);
graph.addEdge(2, 3);
graph.addEdge(3, 1);
System.out.println("All Topological sorts");
graph.allTopologicalSorts();
}
}
انظر أيضًا
مصادر
- صفحة Topological Sorting في توثيق بنى المعطيات في موقع GeeksforGeeks.
- صفحة All Topological Sorts of a Directed Acyclic Graph في توثيق الخوارزميات في موقع GeeksforGeeks.