الفرق بين المراجعتين لصفحة: «Algorithms/binomial random variables»
أنشأ الصفحة ب'<noinclude>{{DISPLAYTITLE:المتغيرات العشوائية ثنائية الحدود}}</noinclude> المتغيرات العشوائية ثنائية الحدود B...' |
لا ملخص تعديل |
||
| سطر 22: | سطر 22: | ||
إنّ احتمالية أن تكون المحاولة ناجحة <code>p</code> لا تعتمد على المحاولات الأخرى؛ لذا سنختار أولًا <code>k</code> محاولة ناجحة وباقي المحاولات <code>n-k</code> ستكون فاشلة؛ وعدد المرات التي يمكن فيها تأدية ذلك هي: | إنّ احتمالية أن تكون المحاولة ناجحة <code>p</code> لا تعتمد على المحاولات الأخرى؛ لذا سنختار أولًا <code>k</code> محاولة ناجحة وباقي المحاولات <code>n-k</code> ستكون فاشلة؛ وعدد المرات التي يمكن فيها تأدية ذلك هي: | ||
[[ملف:binomial random variable.png|مركز]] | |||
ولمّا كانت جميع الأحداث <code>n</code> مستقلة عن بعضها البعض، فإنّ احتمالية الحصول على <code>k</code> محاولة ناجحة من بين <code>n</code> محاولة مساوي لحاصل ضرب احتماليات المحاولات كلّها بعضها ببعض. | ولمّا كانت جميع الأحداث <code>n</code> مستقلة عن بعضها البعض، فإنّ احتمالية الحصول على <code>k</code> محاولة ناجحة من بين <code>n</code> محاولة مساوي لحاصل ضرب احتماليات المحاولات كلّها بعضها ببعض. | ||
وفي هذا المثال هناك <code>k</code> محاولة ناجحة و<code>n - k</code> محاولة فاشلة؛ لذا فإنّ احتمالية كل طريقة في الحصول على <code>k</code> محاولة ناجحة و<code>n - k</code> محاولة فاشلة هي: | وفي هذا المثال هناك <code>k</code> محاولة ناجحة و<code>n - k</code> محاولة فاشلة؛ لذا فإنّ احتمالية كل طريقة في الحصول على <code>k</code> محاولة ناجحة و<code>n - k</code> محاولة فاشلة هي: | ||
[[ملف:binomial random variable2.png|مركز]] | |||
وبهذا فإنّ الاحتمالية النهائية هي: | وبهذا فإنّ الاحتمالية النهائية هي: | ||
| سطر 36: | سطر 32: | ||
ويمكن حساب احتمالية المتغير العشوائي ثنائي الحدود باستخدام العلاقة الرياضية التالية: | ويمكن حساب احتمالية المتغير العشوائي ثنائي الحدود باستخدام العلاقة الرياضية التالية: | ||
[[ملف:binomial random variable3.png|مركز]] | |||
ليكن <code>X</code> متغيرًا عشوائيًا ثنائي الحدود و<code>n</code> عدد المحاولات و <code>p</code> احتمالية الحصول على محاولة ناجحة. | ليكن <code>X</code> متغيرًا عشوائيًا ثنائي الحدود و<code>n</code> عدد المحاولات و <code>p</code> احتمالية الحصول على محاولة ناجحة. | ||
يمكن حساب عدد المحاولات الناجحة بواسطة العلاقة:<br /> | يمكن حساب عدد المحاولات الناجحة بواسطة العلاقة:<br /><syntaxhighlight lang="text"> | ||
E[X] = np | E[X] = np | ||
</syntaxhighlight>ويمكن حساب تفاوت Variance عدد المحاولات الناجحة بواسطة العلاقة:<syntaxhighlight lang="text"> | |||
ويمكن حساب تفاوت Variance عدد المحاولات الناجحة بواسطة العلاقة: | |||
Var[X] = np(1-p) | Var[X] = np(1-p) | ||
</syntaxhighlight> | |||
== تنفيذ الخوارزمية == | == تنفيذ الخوارزمية == | ||
سنفترض تجربة عشوائية متحيزة ترمى فيها عملة معدنية (احتمالية ظهور الرأس = 1/3) عشر مرات في الهواء، والمطلوب حساب احتمالية ظهور الرأس 5 مرات. | سنفترض تجربة عشوائية متحيزة ترمى فيها عملة معدنية (احتمالية ظهور الرأس = <code>1/3</code>) عشر مرات في الهواء، والمطلوب حساب احتمالية ظهور الرأس 5 مرات. | ||
تعرض الشيفرات التالية طريقة حلّ هذه المسألة في عدد من لغات البرمجة: | تعرض الشيفرات التالية طريقة حلّ هذه المسألة في عدد من لغات البرمجة: | ||
| سطر 182: | سطر 175: | ||
System.out.println( " is = " + probability ); | System.out.println( " is = " + probability ); | ||
} | } | ||
} </source> | } </source>تعطي الشيفرات السابقة المخرجات التالية:<syntaxhighlight lang="text"> | ||
Probability of 5 heads when a coin is tossed 10 times where probability of each head is 0.333333 | |||
is = 0.136565 | |||
</syntaxhighlight> | |||
== مصادر == | == مصادر == | ||
مراجعة 18:03، 19 نوفمبر 2019
المتغيرات العشوائية ثنائية الحدود Binomial Random Variables هي نوع خاص من المتغيرات العشوائية المجردة discrete random variables والتي تحسب عدد المرات التي سيقع فيها حدثٌ معين في عدد محدّد من المحاولات.
يجب تحقق الشروط التالية كلّها ليكون المتغير متغيرًا عشوائيًا ثنائي الحدود:
- هناك عدد ثابت من المحاولات (حجم العينة ثابت).
- في كل محاولة، هناك حالتان للحدث المعني، فإمّا أن يقع أو لا يقع.
- احتمالية وقوع (أو عدم وقوع) الحدث متساوية في جميع المحاولات.
- المحاولات مستقلة عن بعضها البعض.
خطوات الخوارزمية
لو فرضنا أنّ:
n = عدد المحاولات
p = احتمالية تحقيق النجاح في كل محاولة
k = عدد المحاولات الناجحة من بين n من المحاولات
ستحاول الخوارزمية معرة احتمالية تحقق k محاولة ناجحة من بين n من المحاولات.
إنّ احتمالية أن تكون المحاولة ناجحة p لا تعتمد على المحاولات الأخرى؛ لذا سنختار أولًا k محاولة ناجحة وباقي المحاولات n-k ستكون فاشلة؛ وعدد المرات التي يمكن فيها تأدية ذلك هي:
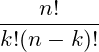
ولمّا كانت جميع الأحداث n مستقلة عن بعضها البعض، فإنّ احتمالية الحصول على k محاولة ناجحة من بين n محاولة مساوي لحاصل ضرب احتماليات المحاولات كلّها بعضها ببعض.
وفي هذا المثال هناك k محاولة ناجحة وn - k محاولة فاشلة؛ لذا فإنّ احتمالية كل طريقة في الحصول على k محاولة ناجحة وn - k محاولة فاشلة هي:
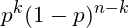
وبهذا فإنّ الاحتمالية النهائية هي:
(عدد الطرق التي يمكن من خلالها الحصول على k محاولة ناجحة و n - k محاولة فاشلة) * (احتمالية كل طريقة في تحقيق k محاولة ناجحة و n - k محاولة فاشلة)
ويمكن حساب احتمالية المتغير العشوائي ثنائي الحدود باستخدام العلاقة الرياضية التالية:
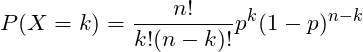
ليكن X متغيرًا عشوائيًا ثنائي الحدود وn عدد المحاولات و p احتمالية الحصول على محاولة ناجحة.
يمكن حساب عدد المحاولات الناجحة بواسطة العلاقة:
E[X] = np
ويمكن حساب تفاوت Variance عدد المحاولات الناجحة بواسطة العلاقة:
Var[X] = np(1-p)
تنفيذ الخوارزمية
سنفترض تجربة عشوائية متحيزة ترمى فيها عملة معدنية (احتمالية ظهور الرأس = 1/3) عشر مرات في الهواء، والمطلوب حساب احتمالية ظهور الرأس 5 مرات.
تعرض الشيفرات التالية طريقة حلّ هذه المسألة في عدد من لغات البرمجة:
- C++:
#include <iostream>
#include <cmath>
using namespace std;
// تحسب الدالة عدد الطرق التي يمكن فيها اختيار r من n عنصر
int nCr(int n, int r)
{
// nCr لما كانت
// nC(n-r) مساوية لـ
// نخفض عدد الدورات في الحلقة التكرارية
if (r > n / 2)
r = n - r;
int answer = 1;
for (int i = 1; i <= r; i++) {
answer *= (n - r + i);
answer /= i;
}
return answer;
}
// تحسب الدالة احتمالية المتغير العشوائي ثنائي الحدود
float binomialProbability(int n, int k, float p)
{
return nCr(n, k) * pow(p, k) *
pow(1 - p, n - k);
}
// اختبار الدالتين السابقتين
int main()
{
int n = 10;
int k = 5;
float p = 1.0 / 3;
float probability = binomialProbability(n, k, p);
cout << "Probability of " << k;
cout << " heads when a coin is tossed " << n;
cout << " times where probability of each head is " << p << endl;
cout << " is = " << probability << endl;
}
- بايثون:
# تحسب الدالة عدد الطرق التي يمكن فيها اختيار r من n عنصر
def nCr(n, r):
# nCr لما كانت
# nC(n-r) مساوية لـ
# نخفض عدد الدورات في الحلقة التكرارية
if (r > n / 2):
r = n - r;
answer = 1;
for i in range(1, r + 1):
answer *= (n - r + i);
answer /= i;
return answer;
# تحسب الدالة احتمالية المتغير العشوائي ثنائي الحدود
def binomialProbability(n, k, p):
return (nCr(n, k) * pow(p, k) *
pow(1 - p, n - k));
# اختبار الدالتين السابقتين
n = 10;
k = 5;
p = 1.0 / 3;
probability = binomialProbability(n, k, p);
print("Probability of", k,
"heads when a coin is tossed", end = " ");
print(n, "times where probability of each head is",
round(p, 6));
print("is = ", round(probability, 6));
- جافا:
import java.util.*;
class GFG
{
// تحسب الدالة عدد الطرق التي يمكن فيها اختيار r من n عنصر
static int nCr(int n, int r)
{
// nCr لما كانت
// nC(n-r) مساوية لـ
// نخفض عدد الدورات في الحلقة التكرارية
if (r > n / 2)
r = n - r;
int answer = 1;
for (int i = 1; i <= r; i++) {
answer *= (n - r + i);
answer /= i;
}
return answer;
}
// تحسب الدالة احتمالية المتغير العشوائي ثنائي الحدود
static float binomialProbability(int n, int k, float p)
{
return nCr(n, k) * (float)Math.pow(p, k) *
(float)Math.pow(1 - p, n - k);
}
// اختبار التابعين السابقين
public static void main(String[] args)
{
int n = 10;
int k = 5;
float p = (float)1.0 / 3;
float probability = binomialProbability(n, k, p);
System.out.print("Probability of " +k);
System.out.print(" heads when a coin is tossed " +n);
System.out.println(" times where probability of each head is " +p);
System.out.println( " is = " + probability );
}
}
تعطي الشيفرات السابقة المخرجات التالية:
Probability of 5 heads when a coin is tossed 10 times where probability of each head is 0.333333
is = 0.136565
مصادر
- صفحة Binomial Random Variables في توثيق الخوارزميات في موقع GeeksforGeeks.