Algorithms/Randomized Algorithms

الخوارزمية العشوائية هي الخوارزمية التي تستخدم عددًا عشوائيًا لتقرّر الخطوة التالية في سير عملها، فعلى سبيل المثال خوارزمية الترتيب السريع العشوائية Randomized Quick Sort، تستخدم الخوارزمية عددًا عشوائيًا لاختيار المحور التالي (أو لتغيير مواقع العناصر في المصفوفة عشوائيًا). يُستفاد من العشوائية عادةً في التقليل من التعقيد الزمني والتعقيد المكاني في الخوارزميات العادية.

مقدمة رياضية

الاحتمالية المشروطة P(A | B)‎ هي احتمالية وقوع الحدث 'A' على افتراض وقوع الحدث 'B' قبله.

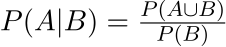
يمكن الاستعانة بالشكل التالي لفهم الصيغة السابقة، إذ لمّا كان الحدث 'B' قد وقع بالفعل، فإنّ فضاء العينة سيتقلّص إلى 'B' فقط؛ ولهذا فإنّ احتمالية وقوع الحدث 'A' ستصبح P(A ∩ B)‎ مقسومًا على P(B)‎.

تربط علاقة بايس Bayes’s forumla بين الاحتماليتين المشروطتين P(A|B)‎ و P(B|A)‎.

علاقة بايس.

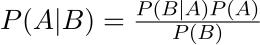
المتغيرات العشوائية

المتغير العشوائي هو دالة تربط نتائج حدث عشوائي (مثل رمي العملة المعدنية) بقيمة حقيقية.

مثال:

لعبة رمي القطعة النقدية:

في هذه اللعبة يحصل اللاعب على 50 نقطة إن كانت نتيجة رمي القطعة النقدية (النقش) ويخسر 50 نقطة إن كانت النتيجة (الكتابة).

يمكن تعريف المتغير العشوائي لعدد النقاط النهائي الذي سيحصل عليه اللاعب كما يلي:

Points = +50 if Head
         -50 if Tail

القيمة المتوقعة للمتغير العشوائي

يمكن تعريف القيمة المتوقعة للمتغير العشوائي R بأنّها:

    E[R] = r1*p1 + r2*p2 + ... rk*pk

تمثل ri قيمة R مع الاحتمالية pi.
ويمكن القول بأنّ القيمة المتوقعة هي مجموع حاصل ضرب الطرفين التاليين (لجميع الأحداث الممكنة):

1. احتمالية الحدث
2. قيمة R في ذلك الحدث.

أمثلة:

• القيمة المتوقعة للنقاط في المثال السابق = 50 * (1/2) + (-50) * (1/2) = 0
• والقيمة المتوقعة لرمي زهر سداسي الوجوه = = 1(1/6) + 2(1/6) + .... + 6*(1/6) = 3.5

خطية التوقع Linearity of Expectations

لنفترض أن R1 و R2 متغيران عشوائيان مجرّدان في فضاء احتمالية معين، فإنّ:

     E[R1 + R2] = E[R1] + E[R2]

القيمة المتوقعة لمجموع الأرقام الناتجة من رمي الزهر ثلاث مرات = ‎3 * 7/2 = 10.5‎

عدد المحاولات المتوقع قبل تحقيق النجاح

إذا كانت احتمالية النجاح في كل محاولة هي p فإن العدد المتوقع للمحاولات قبل تحقيق النجاح هو ‎1/p‎.

لنفترض أنّ سنرمي زهرًا سداسي الوجوه إلى حين الحصول على الرقم 5، فإنّ عدد الرميات المتوقعة قبل الحصول على الرقم 5 هو 6 رميات. لاحظ بأنّ احتمالية الحصول على الرقم 5 هي 1/6 في كل رمية، وبهذا يكون عدد المحاولة ‎1/(1/6)‎ = 6‎.

وفي خوارزمية الترتيب السريع والتي تبحث فيها الخوارزمية عن العناصر المحورية إلى أن تختار العنصر الوسطي n/2 فإنّ عدد المحاولات المتوقعة للعثور لاختيار العنصر الوسطي سيكون 2 وذلك لأنّ احتمالية اختيار أحد العناصر الوسطية هو 1/2.

الخوارزمية العشوائية

الخوارزمية العشوائية هي خوارزمية تستخدم عددًا عشوائيًا لتقرر الخطوة التالية في سير عملها، فعلى سبيل المثال تستخدم خوارزمية الترتيب السريع العشوائية عددًا عشوائيًا لاختيار العنصر الوسطي (pivot) التالي، وهناك خوارزميات لتغيير ترتيب العناصر في المصفوفة عشوائيًا، وتنتخب خوارزمية كاركر Karger's Algorithm ضلعًا بطريقة عشوائية.

تحليل الخوارزميات العشوائية

تمتلك بعض الخوارزميات العشوائية تعقيدًا زمنيًا محدّدًا، فعلى سبيل المثال تمتلك إحدى طرق تنفيذ خوارزمية كاركر تعقيدًا زمنيًا قدره O(E)‎، ومثل هذه الخوارزميات تسمّى بخوارزميات مونتي كارلو Monte Carlo Algorithms ويسهل تحليل هذه الخوارزميات في الحالات السوأى.

وفي المقابل يعتمد التعقيد الزمني لبعض الخوارزميات العشوائية على قيمة المتغير العشوائي، وتسمى هذه الخوارزميات بخوارزميات لاس فيغاس Las Vegas، ويجري تحليل هذه الخوارزميات عادة في الحالات السوأى المتوقعة.

وتتطلب عملية حساب الوقت الذي يتوقع أن تستغرقه الحالة السوأى الأخذ بنظر الاعتبار جميع القيم الممكنة للمتغير العشوائي المستخدم في الحالة السوأى وتقدير الوقت الذي تستغرقه كل قيمة محتملة، ويكون الوقت الذي يتوقع أن تستغرقه الحالة السوأى هو معدّل جميع الأوقات التي جرى تقييمها. ويجدر التنبيه إلى إمكانية الاستفادة من خاصية خطّية التوقعات Linearity of Expectations والعدد المتوقع للمحاولات قبل تحقيق النجاح في تحليل هذا النوع من الخوارزميات.

تصنيف الخوارزميات العشوائية

تصنف الخوارزميات العشوائية إلى صنفين هما:

1. خوارزميات لاس فيغاس Las Vegas Algorithms
2. خوارزميات مونتي كارلو Monte Carlo Algorithms

خوارزميات لاس فيغاس

تعطي هذه الخوارزميات نتائج صحيحة أو مثالية دائمًا، ويعتمد التعقيد الزمني فيها على قيمة عشوائي، ويحسب التعقيد الزمني كقيمة متوقعة expected value. ترتّب خوارزمية الترتيب السريع العشوائي - على سبيل المثال - عناصر المصفوفة المدخلة بتعقيد زمني يتوقّع أن تكون قيمته O(nLogn)‎ في الحالة السوأى.

خوارزميات مونتي كارلو

تعطي هذه الخوارزميات نتائج صحيحة أو مثالية مع بعض الاحتمالية، ويكون التعقيد الزمني لهذا النوع من الخوارزميات العشوائية محدّدًا ويمكن تحليل الحالة السوأى لها بسهولة. فعلى سبيل المثال تنتج إحدى طرق تنفيذ خوارزمية كارك المقطع الأصغر minimum cut مع احتمالية تكون أكبر من ‎1/n^2 (تمثّل n عدد الرؤوس في الرسم البياني)، ويبلغ التعقيد الزمني في الحالة السوأى المقدار O(E)‎. وتعدّ طريقة فيرميت Fermet Method للتحقق من الأعداد الأولية إحدى الأمثلة المعروفة عن خوارزميات مونتي كارلو.

يوضّح المثال التالي الفرق بين التصنيفين:

لنفترض وجود مصفوفة ثنائية Binary array نصف عناصرها 0 والنصف الآخر 1. المطلوب هو إيجاد موقع أي من الوحدات.

تنفيذ هذه المهمة عن طريق خوارزمية لاس فيغاس يتطلب الاستمرار في اختيار عنصر عشوائي إلى حين الوصول إلى الرقم 1. أما خوارزمية مونتي كارلو فستستمر في اختيار عنصر عشوائي إلى حين الوصول إلى الرقم 1 أو الوصول إلى أقصى عدد مسموح به من المحاولات (ليكن k).

تعثر خوارزمية لاس فيغاس دائمًا على موقع للرقم 1، ولكن التعقيد الزمني يكون قيمة غير محدّدة وإنّما متوقعة، إذ إنّ العدد المتوقع للمحاولات قبل تحقيق النجاح هو 2، وهذا يعني أنّ التعقيد الزمني المتوقع هو O(1)‎. أما خوارزمية مونتي كارلو فتعثر على 1 مع احتمالية تقدّر بالقيمة ‎[1 - (1/2)k]‎، ويبلغ التعقيد الزمني المقدار O(k)‎ وهو قيمة محدّدة.

التطبيقات ونطاق الاستخدام

• لنفترض وجود أداة مهمّتها إجراء عملية الترتيب، ولنفترض أنّ هناك عددًا كبيرًا من الأشخاص الذين يستخدمون هذه الأداة مع مصفوفات مرتّبة أصلًا. إن استخدمت الأداة خوارزمية الترتيب السريع العادية (وليست العشوائية) فإنّ هؤلاء المستخدمين سيواجهون الحالة السوأى دائمًا. ولكن إن استخدمت الأداة خوارزمية الترتيب السريع العشوائية، فإنّ التعقيد الزمني الذي سيحصل عليه جميع المستخدمين بدون استثناء هو التعقيد الزمني المتوقّع لهذه الخوارزمية وهو O(n Log n)‎.
• تستخدم الخوارزميات العشوائية استخدامًا واسعًا في عمليات التشفير.
• موازنة الأحمال Load Balancing.
• تطبيقات في علم الأعداد: اختبار الأعداد الأولية.
• بنى المعطيات: التقطيع، الترتيب، البحث، إحصائيات الترتيب Order Statistics، والهندسة الحاسوبية.
• المعادلات الجبرية: متعددات الحدود والمصفوفات. أنظمة البرهنة التفاعلية.
• البرمجة الرياضية: خوارزميات أسرع للبرمجة الخطية، تقريب نتائج البرامج الخطية إلى نتائج البرامج الصحيحة.
• خوارزميات الرسوم البيانية: الشجرة الممتدة الصغرى، المسار الأقصر، المقاطع الصغرى.
• التعداد: بنى المصفوفات ذات العد الاندماجي الدائم Matrix permanent Counting combinatorial structures.
• الحوسبة المتوازية والموزّعة.
• إلغاء العشوائية: تُقترح في البداية خوارزمية عشوائية ثم يجري النقاش حول ما إذا كان بالإمكان إزالة العشوائية للحصول على نتائج محدّدة.

خوارزمية الترتيب السريع العشوائية

تنتخب خوارزمية الترتيب السريع عنصرًا من عناصر المصفوفة المراد ترتيبها وتجعله محورًا pivot لتقسّم بعد ذلك المصفوفة حول هذا العنصر إلى قسمين.

المحور الوسطي Central Pivot هو المحور الذي يقسم المصفوفة إلى قسمين يمتلك أحدهما على الأقل 1/4 من العناصر.

تنتخب خوارزمية الترتيب السريع العشوائية المحور انتخابًا عشوائيًا وفقًا لما يلي:

randQuickSort(arr[], low, high)

تأخذ الدالة المسؤولة عن إجراء الخوارزمية ثلاثة معاملات هي:

1. arr[]‎ : المصفوفة المراد ترتيبها
2. low: موقع البداية
3. high: موقع النهاية

1. إن كان low >= hight تتوقف الدالة عن العمل.
2. تنفّذ الخطوات التالية ما لم يكن المحور x محورًا عنصريًا:
   1. اختيار رقم عشوائي من مجموعة الأرقام [low..high]، وليكن الرقم المنتخب x.
   2. عدّ العناصر في المصفوفة arr[low..high]‎ التي تكون أصغر من العنصر arr[x]‎. وليكن sc.
   3. عدّ العناصر في المصفوفة arr[low..high]‎ التي تكون أكبر من العنصر arr[x]‎، وليكن gc.
   4. ليكن n = (high - low + 1)‎. إن كان sc >= n/4 وكان gc >= n/4 فإنّ x هو المحور الوسطي.
3. تقسيم المصفوفة arr[low..high]‎ حول المحور x.
4. تنفيذ الخطوات السابقة تعاوديًا على العناصر الأصغر.
   

randQuickSort(arr, low, sc-1)‎

1. تنفيذ الخطوات السابقة تعاوديًا على العناصر الأكبر.
   

randQuickSort(arr, high-gc+1, high)‎

إنّ أهمّ خطوة في عملية تحليل خوارزمية الترتيب السريع العشوائي هو الوقت الذي تستغرقه الخطوة الثانية وهو O(n)‎، إذ يجب معرفة عدد الدورات التي ستمرّ بها الحلقة التكرارية قبل العثور على المحور الوسطي.

إن احتمالية أن يكون العنصر المنتخب عشوائيًا هو المحور الوسطي هي 1/2؛ ولهذا فإنّ عدد الدورات التي ستمرّ بها حلقة while التكرارية هي 2، وبهذا يمكن القول أنّ التعقيد الزمني المتوقع للخطوة الثانية هو O(n)‎.

التعقيد الزمني للحالة السوأى

تقسم المصفوفة في الحالة السوأى إلى قسمين، يمتلك أحدهما n/4 من العناصر والآخر 3n/4 من العناصر. ويبلغ التعقيد الزمني حينئذٍ المقدار O(Log n)‎.

يجدر التنبيه إلى أنّ طريقة التنفيذ السابقة ليست هي الطريقة المثلى، وإنّما هي لتوضيح سهولة عملية تحليل الخوارزمية. تنفّذ خوارزمية الترتيب السريع العشوائية عادة باختيار عنصر عشوائية كمحور (دون استخدام الحلقات التكرارية)، أو بتغيير مواقع العناصر في المصفوفة، ويبلغ التعقيد الزمني المتوقع في الحالة السوأى لهذه الخوارزمية المقدار O(n Log n)‎، ولكن تحليل الخوارزمية يكون أكثر تعقيدًا.

المتغيرات العشوائية ثنائية الحدود

المتغيرات العشوائية ثنائية الحدود Binomial Random Variables هي نوع خاص من المتغيرات العشوائية المجردة discrete random variables والتي تحسب عدد المرات التي سيقع فيها حدثٌ معين في عدد محدّد من المحاولات.

اقتراح كلمات مرور قوية

تتحقق هذه الخوارزمية من قوة كلمة المرور التي يدخلها المستخدم، وتقترح عليه عددًا منها إن لم تكن كلمة المرور التي أدخلها قوية.

مصادر

• صفحة Randomized Algorithms | Set 0 (Mathematical Background) في توثيق الخوارزميات في موقع GeeksforGeeks.
• صفحة Randomized Algorithms | Set 1 (Introduction and Analysis) في توثيق الخوارزميات في موقع GeeksforGeeks.
• صفحة Randomized Algorithms | Set 2 (Classification and Applications) في توثيق الخوارزميات في موقع GeeksforGeeks.